Feb 07, 2024 | 9 min read

\( \newcommand{\bra}[1]{\langle #1|} \) \( \newcommand{\ket}[1]{|#1\rangle} \) \( \newcommand{\braket}[2]{\langle #1|#2\rangle} \) \( \newcommand{\i}{{\color{blue} i}} \) \( \newcommand{\Hil}{{\cal H}} \) \( \newcommand{\cg}[1]{{\rm C}#1} \) \( \newcommand{\lp}{\left(} \) \( \newcommand{\rp}{\right)} \) \( \newcommand{\lc}{\left[} \) \( \newcommand{\rc}{\right]} \) \( \newcommand{\lch}{\left\{} \) \( \newcommand{\rch}{\right\}} \) \( \newcommand{\Lp}{\Bigl(} \) \( \newcommand{\Rp}{\Bigr)} \) \( \newcommand{\Lc}{\Bigl[} \) \( \newcommand{\Rc}{\Bigr]} \) \( \newcommand{\Lch}{\Bigl\{} \) \( \newcommand{\Rch}{\Bigr\}} \) \( \newcommand{\rqa}{\quad \Rightarrow \quad} \)

2. Explicación geométrica

Para facilitar la explicación y sin perdida de generalidad, pongámonos en el caso más simple de todos: queremos encontrar una única solución \(| \omega_0 \rangle\) y tenemos \(N=2^n\). Supongamos también que podemos partir del caso más simple, de una superposión uniforme de todos los estados. Más adelante iremos viendo generalizaciones del algoritmo para casos más complicados, como el caso de varias soluciones o el caso en el que partimos de una distribución de probabilidad aleatoria.

Estado inicial: superposición

Partimos de una superposición uniforme de \(N\) estados

(7)\[\begin{equation} | \Psi_0 \rangle = \frac{1}{\sqrt{N}} \sum_{i=0}^{N} | i \rangle. \end{equation} \]

Esto no es más que decir que al inicio de la búsqueda, todas las opciones son igualmente probables (cualquier suposición de la ubicación de la solución es tan buena como cualquier otra).

Nota

Recordemos que si \(N=2^n\), donde \(n\) es el número de qubits, este estado es fácil de construir, pues solo tenemos que aplicar puertas de Hadamard en todos los Qubits (partiendo estos del estado \(|0 \rangle\)):

(8)\[\begin{equation} |\Psi_0 \rangle = H^{\otimes n} |0 \rangle^{n} = \frac{1}{\sqrt{N}} \sum_{i=0}^{N=2^n} | i \rangle. \end{equation} \]

El objetivo del algoritmo de Grover es aumentar el valor del coeficiente que acompaña al estado \(| \omega_0 \rangle\) que queremos encontrar, es decir, aumentar la probabilidad de que al medir, obtengamos este estado. Como la suma de todas las probabilidades tiene que ser 1, este aumento en la probabilidad del estado \(| \omega_0 \rangle\) se produce a expensas de reducir la probabilidad del resto.

Nota

Recordemos que en mecánica cuántica podemos tener un estado que sea la superposición de varios estado (como es el caso anterior), pero al medir solo obtenemos uno de estos estado. La probabilidad de medir cada uno de estos estados que forman la superposición es igual al módulo cuadrado del coeficiente que lo acompaña en el vector de estado \(| \Psi \rangle\) (el módulo cuadrado de la amplitud). Este caso, vemos que todos los estados tiene probabilidad \(1/N\).

Amplificación de amplitud mediante iteraciones del algoritmo

Como vamos a ver a continuación, el algoritmo de Grover tiene una interpretación geométrica muy simple: dos reflexiones que rotan el vector de estado en un plano bidimensional.

El algoritmo de Grover consta de dos partes: un oráculo y un difusor. Para que el algoritmo maximice la probabilidad de la solución deseada tenemos realizar un número concreto de \textbf{iteraciones}. En cada iteración del algoritmo, primero se aplica el oráculo y después el difusor. Con cada iteración la probabilidad de medir la solución deseada va aumentando. Sin embargo, es muy importante aplicar el número correcto de iteraciones que nos maximiza la probabilidad, pues tanto si nos quedamos cortos como si nos pasamos, la probabilidad de medir \(|\omega_0 \rangle\) disminuye. Esto se va a entender muy bien a continuación, cuando veamos la explicación geométrica.

Pongamos el estado inicial de la Ec. (7) de una forma más adecuada para nuestro propósito

(9)\[\begin{equation} \boxed{|\Psi_0 \rangle = | \Psi (k(0),l(0)) \rangle = k(0) |\omega_0 \rangle + \sum_{i \neq \omega_0} l(0) |i \rangle}, \quad \text{donde} \quad \boxed{k(0) = l(0) = \frac{1}{\sqrt{N}}}. \end{equation} \]

Denominaremos \(k(t)\) y \(l(t)\) a los coeficientes que tendremos en la t-esima iteración del algoritmo, es decir

(10)\[\begin{equation} \boxed{|\Psi(t) \rangle = | \Psi (k(t),l(t)) \rangle = k(t) |\omega_0 \rangle + \sum_{i \neq \omega_0}^N l(t) |i \rangle }. \end{equation} \]

Véase que aquí ya estamos adelantando que los coeficientes de todos los estados que no son el deseado son iguales en cada iteración. Nuestro vector de estado \(|\Psi(t) \rangle\) vive en un espacio de Hilbert de \(N\) dimensiones y los estados \(| i \rangle\), con \(i=0,1,\dots,N-1\) , forman una base ortogonal del espacio de Hilbert (véase que aquí se incluye \(\omega_0\), pues no es nada más que un valor de \(i\) concreto). Para entender bien esto, podemos fijamos en las ecuaciones anteriores (Ec. (7) y Ec. (9)) y ver que estas no son más que la expresión de un vector como la multiplicación de unos coeficientes por los elementos de la base\footnote{Esto es en esencia lo mismo que con vectores en tres dimensiones: \(\vec{r} = a \hat{x} + b \hat{y} + c \hat{z}\)}. Como no podemos dibujar un vectores de más de 3 dimensiones, para explicar geométricamente el algoritmo vamos a recurrir a un truco: vamos a descomponer nuestro vector de estado en la suma de dos vectores \(|\omega_0 \rangle\) y \(| \omega^{\perp} \rangle\), donde este último es la suma de todos los demás elementos de la base, es decir:

(11)\[\begin{equation} \boxed{|\Psi(t) \rangle = | \Psi (k(t),l(t)) \rangle = k(t) |\omega_0 \rangle + l(t) \sqrt{N-1} | \omega^{\perp} \rangle}, \qquad \text{donde} \qquad \boxed{| \omega^{\perp} \rangle = \frac{1}{\sqrt{N-1}}\sum_{i \neq \omega_0}^N |i \rangle}. \end{equation} \]

Nota

Es importante darse cuenta de donde sale el factor \(\sqrt{N-1}\) en la definición de \(|\omega^{\perp}\rangle\). Este es debido a que estamos definiendo \(|\omega^{\perp}\rangle\) como un vector unitario, es decir

(12)\[\begin{equation} \langle \omega^{\perp}| \omega^{\perp} \rangle = 1. \end{equation}\]

Por otro lado, \(|\Psi_0\rangle\) también es unitario

(13)\[\begin{equation} \parallel |\Psi(t) \rangle \parallel^2 = \langle \Psi(t) | \Psi(t) \rangle = k(t)^2 + \sum_{i \neq \omega_0}^N l(t)^2 = k(t)^2 + l(t)^2 (N-1) = 1 . \end{equation}\]

Con lo cual, ese factor es necesario.

Teniendo en cuenta que \(|\omega_0 \rangle\) es un elemento de la base, eso quiere decir que es ortogonal al resto de elementos de la base. Concluimos entonces que \(|\omega_0 \rangle\) y \(| \omega^{\perp} \rangle\) son ortogonales. Podemos pues dibujar nuestro vector de estado en un plano cuyos ejes son \(|\omega_0 \rangle\) y \(|\omega^{\perp} \rangle\). La imagen de la izquierda de la Fig. 1 podemos ver el estado inicial \(| \Psi_0 \rangle\) dibujado en este plano.

Nota

Veamos un ejemplo sencillo para ver a que nos referimos con esta descomposición. Pongamos que tenemos un vector tridimensional unitario de la forma

\[ \vec{r} = a \vec{x} + b \vec{y} + c \vec{z}, \quad \text{ donde } a^2+b^2+c^2 = 1 .\]

y donde \(\vec{x}\), \(\vec{y}\) y \(\vec{z}\) son los vectores unitarios en las direcciones de los ejes \(X\), \(Y\) y \(Z\). Estos vectores unitarios son los \textbf{elementos de la base} que comentamos anteriormente (los equivalentes a los estados \(|i\rangle\) en \(\mathbb{R}^3\)). Supongamos ahora que nuestra solución es \(\vec{z}\). Lo que podemos hacer es juntar \(a \vec{x} + b \vec{y}\) en un único vector unitario \(\vec{v}\) que represente al plano formado por \(\vec{x}\) y \(\vec{y}\)

\[ \vec{v} = \frac{1}{\sqrt{a^2+b^2}} \lp a \vec{x} + b \vec{y} \rp. \]

Con lo que

\[ \vec{r} = c \vec{z} + \sqrt{a^2+b^2} \, \vec{v}. \]

De esta forma, al aumentar \(c\) el vector \(r\) se va poniendo cada vez más paralelo al eje \(Z\), mientras que si aumentamos \(a\) o \(b\) el vector se acerca a \(\vec{v}\), que representa el plano \(XY\).

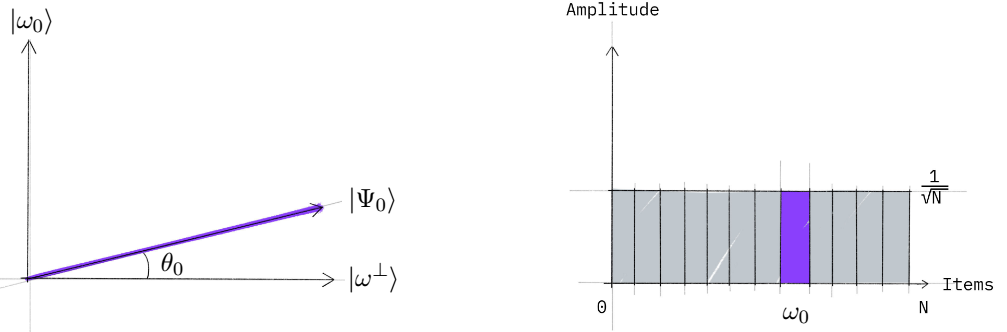
Fig. 1 Estado inicial del algoritmo de Grover: superposición uniforme de los \(N\) estados. En la figura de la izquierda, \(| \Psi_0 \rangle\) representa el estado inicial, el eje \(|\omega_0 \rangle \) representa la solución y el eje \(| \omega^{\perp} \rangle\) el resto de estados de espacio de Hilbert. En la figura de la derecha vemos la \textbf{amplitud} de cada estado. Recordemos que la probabilidad de cada estado es el cuadrado de la amplitud. Figura tomada de [16].

Sabemos también que todo vector en un plano podemos definirlo mediante su módulo y el ángulo respecto a uno de los ejes. Como el vector de estado tiene módulo uno (la suma de las probabilidades es uno), podemos escribirlo solo en función de un ángulo. Si llamamos \(\theta_0\) al ángulo que forman el vector de estado con el eje \(| \omega^{\perp} \rangle\), podemos escribir

(14)\[\begin{equation} | \Psi_0 \rangle = \sin \theta_0 \, |\omega_0 \rangle + \cos \theta_0 \, | \omega^{\perp} \rangle, \qquad \text{donde} \qquad \boxed{\sin \theta_0 = \frac{1}{\sqrt{N}}}. \end{equation} \]

En el gráfico de barras de la derecha en la Fig. 1 podemos ver las amplitudes de los estados. Recordemos que la probabilidad de un estado es el cuadrado de la amplitud.

Primera parte de las iteraciones: El oráculo.

El algoritmo de Grover usa un \textbf{oráculo} cuya función es aplicar una fase negativa al estado que buscamos, es decir

(15)\[\begin{split}\begin{equation} \boxed{U_{\omega_0} | i \rangle = \lch \begin{matrix} & | i \rangle \quad \text{si } i \neq \omega_0 \\ & - | i \rangle \quad \text{si } i = \omega_0. \end{matrix} \right.} \end{equation} \end{split}\]

Este oráculo no es más que una matriz diagonal con todo 1 en la diagonal menos en el elemento correspondiente al estado \(| \omega_0 \rangle\), donde tenemos un \(-1\). Veremos más adelante ejemplos de como construir este tipo de oráculos. Podemos adelantar que, aunque no es trivial construirlos pues a priori parece que tenemos que conocer la solución de antemano, tampoco es (en muchos caso) excesivamente complicado.

Una de las características importantes de este algoritmo es lo fácil que resulta convertir un problema a un oráculo de esta forma. Hay muchos problemas computacionales en los que es difícil encontrar una solución, pero relativamente fácil verificarla (problemas NP). Por ejemplo, podemos verificar fácilmente la solución de un sudoku comprobando que se cumplen todas las reglas. Para estos problemas, podemos crear una función \(f\) que tome una propuesta de solución \(i\) y nos devuelva \(f(i)=0\) si \(i\) no es solución (\(i \neq \omega_0\)) y \(f(i) = 1\) si \(i\) es solución (\(i \neq \omega_0\)). Podemos entonces definir el oráculo de la forma

(16)\[\begin{equation} \boxed{U_{\omega_0} |i \rangle = (-1)^{f(i)} |i \rangle}. \end{equation} \]

De esta forma, a matriz es ahora una matriz diagonal con

(17)\[\begin{equation} Diag(U_{\omega_0})=\lc (-1)^{f(0)}, \, (-1)^{f(1)}, \dots , \, (-1)^{f(2^n-1)} \rc . \end{equation}\]

Nota (Retorno de fase -phase kickback-)

Podemos usar el retorno de fase (phase kickback) para construir este tipo de oráculos. Si tenemos nuestra función clásica \(f(x)\), podemos convertirla en un circuito reversible de la forma

\[\begin{equation*} |x \rangle |0 \rangle \rightarrow |x \rangle | 0 \oplus f(x) \rangle = |x \rangle | f(x) \rangle . \end{equation*}\]

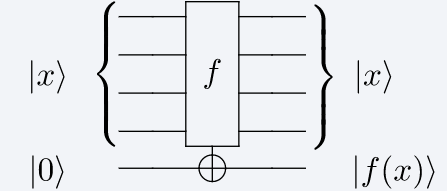
Si inicializamos la ancilla en el estado \(| -\rangle\), tenemos (ver la segunda figura)

\[\begin{equation*} |x \rangle |- \rangle = \frac{1}{\sqrt{2}} |x \rangle \lp | 0 \rangle - | 1 \rangle \rp \rightarrow |x \rangle \lp | 0 \oplus f(x) \rangle - | 1 \oplus f(x) \rangle \rp = (-1)^{f(x))} |x \rangle |- \rangle . \end{equation*}\]

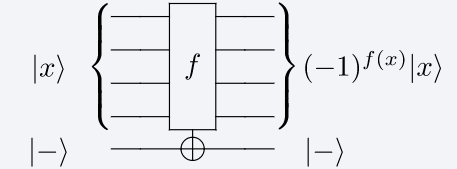
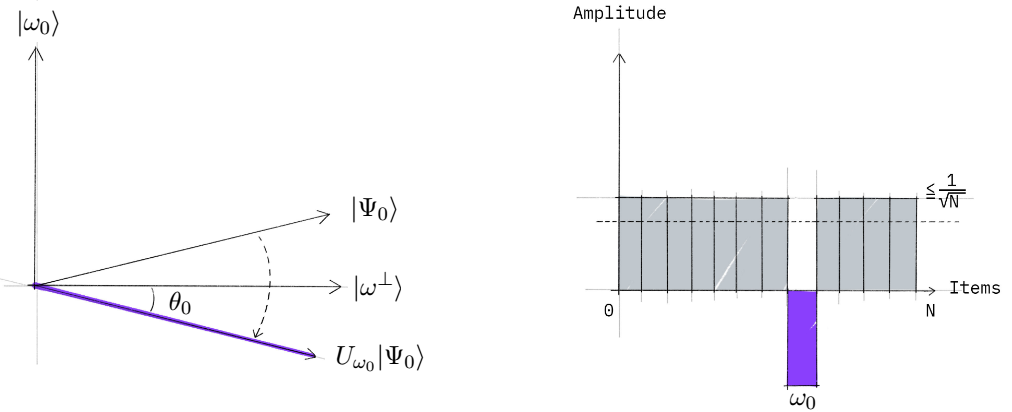
Fig. 2 Primer paso del algoritmo de Grover: aplicación del \textbf{oráculo} \(U_{\omega_0}\) para cambiar el signo de la amplitud del estado deseado. En la figura de la izquierda, \(| \Psi_0 \rangle\) representa el estado inicial, el eje \(|\omega_0 \rangle \) representa la solución y el eje \(| \omega^{\perp} \rangle\) el resto de estados de espacio de Hilbert. En la figura de la derecha vemos la \textbf{amplitud} de cada estado, donde la línea punteada representa la media. Figura tomada de [16].

En la Fig. 2 podemos ver el efecto del oráculo \(U_{\omega_0}\) sobre el vector y las amplitudes. El cambio de signo en la amplitud del estado \(| \omega_0 \rangle\) se traduce en un cambio de signo en la proyección del vector de estado sobre este eje. A efectos prácticos, esto no es más que una reflexíón del vector de estado respecto al eje \(| \omega^{\perp} \rangle\). Como las probabilidades son el cuadrado de las amplitudes, este cambio de signo no se traduce en un cambio en la probabilidades. A efectos de las medidas, nada ha cambiado. En esta figura también se representa la media de las amplitudes (linea punteada). Vemos que ha disminuido la media al cambiar el signo de la amplitud del estado \(| \omega_0 \rangle\).

Segunda parte de las iteraciones: El difusor.

El difusor consiste en aplicar el operador

(18)\[\begin{equation} \boxed{U_{\Psi_0} = 2 |\Psi_0 \rangle \langle \Psi_0 | - I }. \end{equation} \]

Este operador no es más que una reflexión respecto el esto inicial \(|\Psi_0 \rangle\).

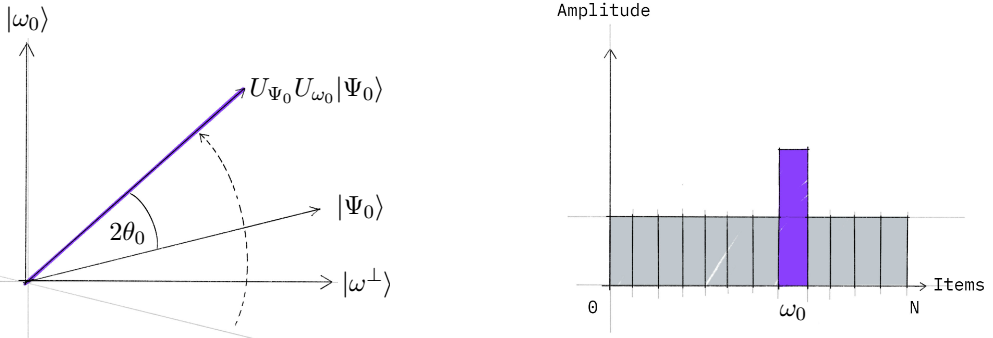
Fig. 3 Segundo paso del algoritmo de Grover: aplicar el operador de \textbf{difusión} (o reflexión) \(U_{\Psi_0} = 2 |\Psi_0 \rangle \langle \Psi_0 | - I\). En la figura de la izquierda, \(| \Psi_0 \rangle\) representa el estado inicial, el eje \(|\omega_0 \rangle \) representa la solución y el eje \(| \omega^{\perp} \rangle\) el resto de estados de espacio de Hilbert. En la figura de la derecha vemos la amplitud de cada estado. Recordemos que la probabilidad de cada estado es el cuadrado de la amplitud. Figura tomada de [16].

En la Fig. 3 podemos ver el efecto del difusor. En el diagrama de barras de la amplitud, podemos entender esta transformación como una reflexión respecto a la media de las amplitudes (la media queda igual). Como habíamos disminuido la media al aplicar el oráculo, lo que tenemos ahora es una amplificación de la amplitud del estado deseado. Esto se ve también en el plano de la izquierda, pues las amplitudes no son más que las proyecciones del vector sobre los ejes.

Lo que estamos haciendo mediante la aplicación del oráculo y el difusor no es mas que rotar el vector de estado un ángulo \(2 \theta_0\) (donde \(\theta_0\) está definido en la Ec. (14)) hacia el eje que representa nuestra solución, aumentando así su proyección, es decir, su amplitud, y con ello la probabilidad de medirlo.

Después de \(t\) iteraciones hemos aumentado el ángulo en \(2t\theta_0\), con lo que tenemos estado:

(19)\[\begin{equation} \boxed{|\Psi(t) \rangle = \lp U_{\Psi_0} U_{\omega_0} \rp^t | \Psi_0 \rangle} = \sin \lp (2t+1) \theta_0 \rp \, |\omega_0 \rangle + \cos \lp (2t+1) \theta_0 \rp \, | \omega^{\perp} \rangle. \end{equation} \]

Podemos ahora definir el operador de Grover

(20)\[\begin{equation} \boxed{G = U_{\Psi_0} U_{\omega_0}} \rqa |\Psi(t) \rangle = G^t | \Psi_0 \rangle. \end{equation}\]

Ahora es fácil entender porqué tenemos que aplicar un número concreto de iteraciones y porqué si nos pasamos, la probabilidad disminuye. Como acabamos de ver, el resultado después de cada iteración es que rotamos el vector de estado \(2 \theta_0\) en el sentido contrario de las agujas del reloj. Lo que queremos es que el vector quede lo más vertical posible, es decir, que quede lo más cerca posible del eje \(|\omega\rangle \). Si hacemos demasiadas iteraciones, lo que vamos a conseguir es “pasarnos de largo” del eje. Discutiremos el número exacto de iteraciones en la sección 3. Número conocido de soluciones, pero ya comentamos que es del orden de \(\sqrt{N}\).

Si comparamos la Ec. (11) y la Ec. (19) vemos que

(21)\[\begin{align} & \boxed{k(t) = \sin \Lc (2t+1) \theta_0 \Rc} & \boxed{l(t) = \frac{1}{\sqrt{N-1}}\cos \Lc (2t+1) \theta_0 \Rc}. \end{align} \]

---

Autores:

David Castaño (UMA-SCBI), Raul Fuentes (BSC-CNS), Daniel Talaván (COMPUTAEX), Francisco Matanza (UNICAN)

---

License: Licencia Creative Commons Atribución-CompartirIgual 4.0 Internacional.

This work has been financially supported by the Ministry for Digital Transformation and of Civil Service of the Spanish Government through the QUANTUM ENIA project call - Quantum Spain project, and by the European Union through the Recovery, Transformation and Resilience Plan - NextGenerationEU within the framework of the Digital Spain 2026 Agenda.