Apr 12, 2024 | 5 min read

\( \newcommand{\bra}[1]{\langle #1|} \) \( \newcommand{\ket}[1]{|#1\rangle} \) \( \newcommand{\braket}[2]{\langle #1|#2\rangle} \) \( \newcommand{\i}{{\color{blue} i}} \) \( \newcommand{\Hil}{{\cal H}} \) \( \newcommand{\cg}[1]{{\rm C}#1} \) \( \newcommand{\lp}{\left(} \) \( \newcommand{\rp}{\right)} \) \( \newcommand{\lc}{\left[} \) \( \newcommand{\rc}{\right]} \) \( \newcommand{\lch}{\left\{} \) \( \newcommand{\rch}{\right\}} \) \( \newcommand{\Lp}{\Bigl(} \) \( \newcommand{\Rp}{\Bigr)} \) \( \newcommand{\Lc}{\Bigl[} \) \( \newcommand{\RC}{\Bigr]} \) \( \newcommand{\Lch}{\Bigl\{} \) \( \newcommand{\Rch}{\Bigr\}} \) \( \newcommand{\rqa}{\quad \Rightarrow \quad} \)

5. Conteo de soluciones (Quantum counting)

En esta sección vamos a ver un algoritmo para obtener el número \(M\) de soluciones. Este algoritmo puede decirse que en cierta medida está inspirado en el algoritmo de Shor, pues lo que vamos a hacer es usar el \textbf{algoritmo de estimación de fase cuántico (QPE)} para obtener el ángulo \(\theta\) a partir del operador de Grover \(G\). Después, podemos usar la Ec. (29) para obtener \(M\) partir de \(\theta\).

Vamos a seguir en el caso en el que \(N=2^n\) y la distribución de probabilidad inicial es uniforme.

Breve resumen de la estimación de fase cuántica (QFE).

Dado un operador unitario \(U\) y un autovector \(\left| \psi \right\rangle\) del mismo, tenemos:

\[ U \left| \psi \right\rangle = e^{2 \pi i \alpha} \left| \psi \right\rangle \]

El \textbf{algoritmo de estimación de fase cuántica} lo que hace es calcular un valor aproximado del ángulo \(\alpha\). En la Fig. 4 podemos ver el circuito que implementa este algoritmo. No vamos a entrar a hablar en detalle del mismo (puede verse una explicación más detallada en las notas del algoritmo de Shor). Simplemente comentar dos cosas:

• Por el registro de qubits de abajo en la Fig. 4 debe de entrar el autoestado de \(U\) del cual queremos medir la fase.

• Si por el registro de conteo entran \(p\) qubits (el de arriba en la Fig. 4), en la salida vamos a medir el estado \(| 2^p \alpha \rangle\).

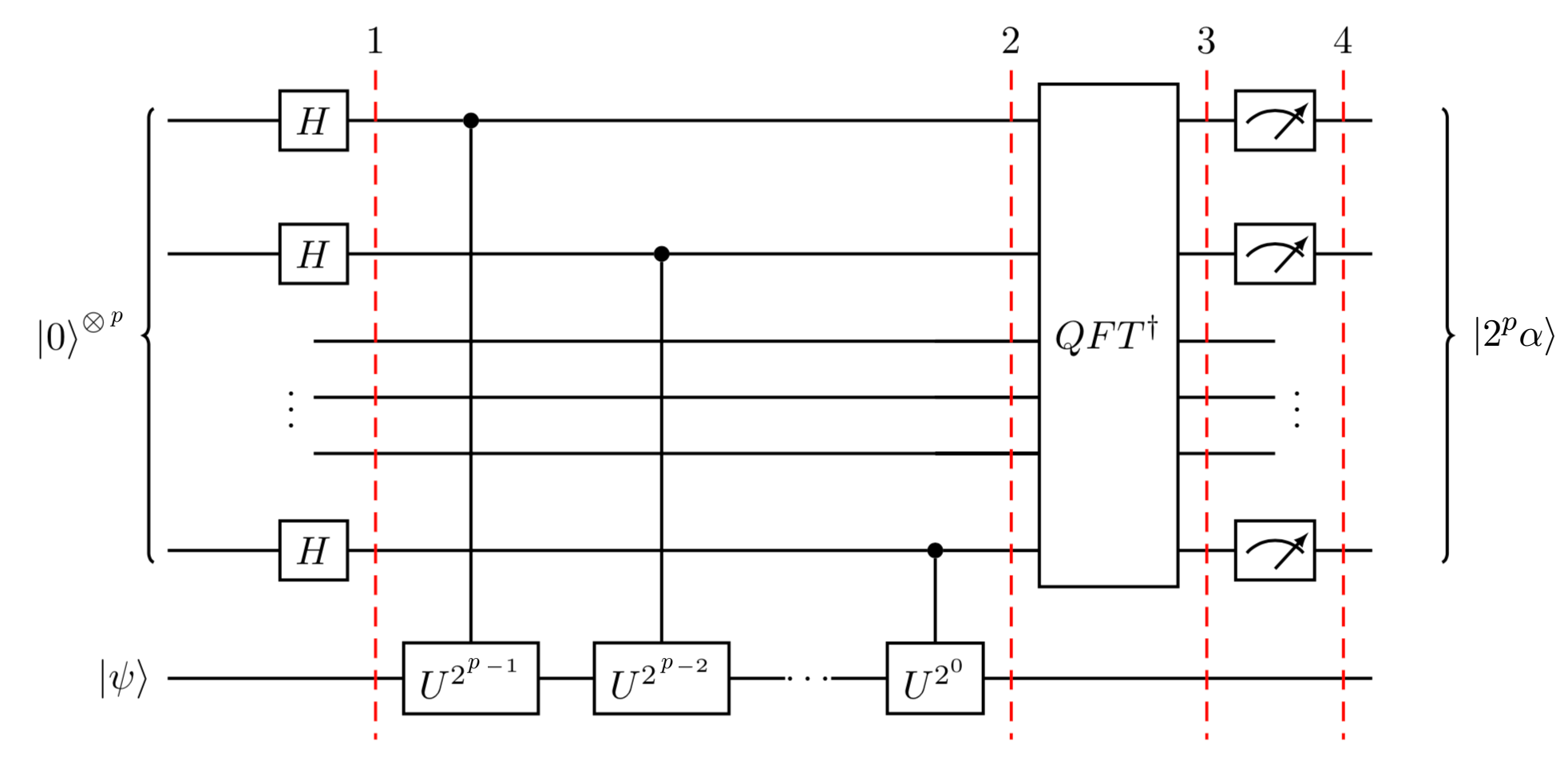
Fig. 4 Implementación del algoritmo de estimación de fase cuántica (en el convenio estándar, siendo el bit más significativo el de arriba).

Para más información soble la QPE, puede verse [6]

Estimación de fase con el operador de Grover.

Como ya comentamos anteriormente, el operador de Grover \(G\) (ver Ec. (32)) rota el vector de estado en un ángulo \(2\theta\), donde \(\theta\) está dado por la Ec. (29), es decir

(58)\[\begin{equation} |\Psi(t+1) \rangle = G | \Psi(t) \rangle = e^{i 2 \theta} | \Psi(t) \rangle. \end{equation}\]

En concreto, se puede aplicar sobre el estado inicial

(59)\[\begin{equation} \boxed{G | \Psi_0 \rangle = e^{i 2 \theta} | \Psi_0 \rangle}, \qquad \text{ donde } \qquad | \Psi_0 \rangle = H^{\otimes n} |0\rangle = \frac{1}{2^n} \sum_{i=0}^{2^n} | i \rangle \end{equation}\]

Podemos pues usar el algoritmo de QFE poniendo el registro de abajo en el estado \(| \Psi_0 \rangle \) y mediremos a la salida el estado \(| 2^p 2 \theta / 2 \pi \rangle = | 2^p \theta / \pi \rangle\). Podemos ver esto en la Fig. 5.

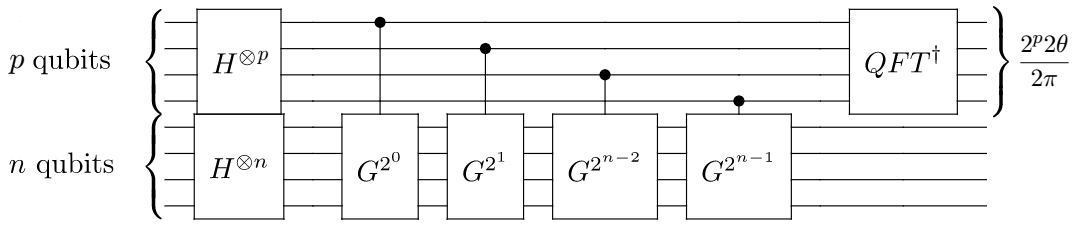
Fig. 5 Circuito para la QFE en el caso de Grover.

Como acabamos de comentar, al aplicar QFE mediremos un valor \(\tilde{f} = 2^p\tilde{\theta} / \pi\). Podemos despejar \(\tilde{\theta}\) y usar Ec. (29) para calcular \(\tilde{M}\)

(60)\[\begin{equation} \tilde{\theta} = \frac{\tilde{f} \pi}{2^p} \rqa \tilde{M} = 2^n \, \sin^2 \tilde{\theta} = 2^n \, \sin^2 \frac{\tilde{f} \pi}{2^p}, \end{equation} \]

donde las \(\tilde{\theta}\), \(\tilde{f}\) y \(\tilde{M}\) llevan una tilde para diferenciarlos de los valores reales. Esto es, porque dependiendo del como de grande sea \(p\) (cuantos qubits tengamos en el registro de conteo) nos acercaremos más a medir el valor real del ángulo \(\theta\).

Nota

Como veremos en la Creación de un difusor U_{\Psi_0}., muchas veces en vez de implementar el operador de difusión \(U_{\Psi_0}\) (ver Ec. (31)) en realidad se implementa \(-U_{\Psi_0}\). En una búsqueda de Grover normal, esta fase es global y no afecta al resultado, pero ahora estamos aplicando versiones controladas del operador de Grover \(G\), con lo que esta fase afecta. En esencia, el único cambio es que en realidad estamos contando aquellos estados que \textit{no son solución}. Lo único que tenemos que hacer para obtener el número de soluciones es restar al total de estados, \(N\), el valor que obtenemos de aplicar QFE.

Precisión de \(\tilde{M}\) respecto a \(M\).

En esta sección vamos a seguir el artículo [2].

Podemos evaluar la precisión del valor de \(\tilde{M}\) respecto al valor real \(M\), acotando la desviación entre los mismos a medida que variamos \(p\). Para ello, vamos a empezar asumiendo que la diferencia entre el valor real y el medido es menor que uno, es decir, \(| f- \tilde{f}| <1\). Esto sucede con una probabilidad razonable si \(f\) es suficientemente grande (si \(p\) es suficientemente grande). Teniendo en cuenta la Ec. (60), vemos que

\[\begin{equation*} | f- \tilde{f}| < 1 \rqa | \theta - \tilde{\theta}| < \frac{\pi}{2^p} \rqa | \sin \theta - \sin \tilde{\theta}| < \frac{\pi}{2^p}, \end{equation*}\]

donde en la última expresión se ha tenido en cuenta que \(\sin \theta \approx \theta\) si \(\theta\) es pequeño, lo cual es lógico si consideramos \(M << N\). Jugando con las desigualdades puede verse que

(61)\[\begin{equation} \boxed{|M - \tilde{M}| < \frac{2 \pi}{2^p} \sqrt{M N} + \frac{\pi^2}{(2^p)^2} N}. \end{equation} \]

Nota

Teniendo en cuenta las desigualdades anteriores, podemos derivar la expresión deseada

\[\begin{equation*} M - \tilde{M}| \lt N \left| sin^2 \theta - sin^2 \tilde{\theta} \right| = N \left| \sin \theta - \sin \tilde{\theta} \right| \left| \sin \theta + \sin \tilde{\theta} \right| \lt N \frac{\pi}{2^p} \lp \sin \theta + \sin \tilde{\theta} \rp. \end{equation*}\]

En la última igualdad hemos quitado el valor absoluto porque es una suma de dos términos positivos (\(0 < \theta < \pi/2\)). Precisamente, como estos dos senos son positivos podemos escribir

\[\begin{equation*} \left| \sin \theta - \sin \tilde{\theta} \right| \lt \frac{\pi}{2^p} \rqa \lch \begin{matrix} & \sin \tilde{\theta} \lt \sin \theta + \frac{\pi}{2^p} \\ & \sin \theta \lt \sin \tilde{\theta} + \frac{\pi}{2^p} . \end{matrix} \right. \end{equation*}\]

Esto es porque tenemos dos números positivos que se diferencian en menos de una cierta cantidad \(\alpha\), así que es siempre cierto que la suma de uno de los números más \(\alpha\) es mayor que el otro. Podemos usar la primera de estas desigualdades para seguir con el cálculo

(62)\[\begin{equation} |M - \tilde{M}| \lt N \frac{\pi}{2^p} \lp \sin \theta + \sin \tilde{\theta} \rp \lt N \frac{\pi}{2^p} \lp 2 \sin \theta +\frac{\pi}{2^p} \rp \end{equation}\]

Finalmente, llegamos a la Ec. (61)

Como podemos ver, la precisión depende de \(p\). Además, el tiempo de ejecución depende de \(p\), con lo que lo ideal es elegir un valor de \(p\) suficientemente grande como para tener una buena precisión, pero que este valor de \(p\) no sea demasiado grande y el algoritmo no tarde demasiado. Tomemos \(c\) como un parámetro y veamos diferentes casos:

• Si tomamos \(2^p = c \sqrt{N}\), el error de nuestra estimación de \(M\) esta acotado por \(\frac{2 \pi}{c} \sqrt{M} + \frac{\pi^2}{c^2}\) siempre que \(|f - \tilde{f}| < 1\). Esto recuerda a encontrar la respuesta hasta unas pocas desviaciones estándar.

• Si nos conformamos con tener un error \textit{relativo} pequeño, podemos correr el algoritmo para sucesivos valores de \(p\) hasta que \(\tilde{f}\) sea razonablemente grande. Esto sucederá cuando \(2^p = c \sqrt{N/M}\). Después de un tiempo proporcional a \(\sqrt{N/M}\), esto nos dará una estimación para \(M\) que probablemente estén dentro de un factor \((1+ \pi/c)^2\) de la respuesta correcta.

• Si queremos que el error \textit{absoluto} esté probablemente limitado por una constante, aplicamos el algoritmo una vez para \(2^p = c \sqrt{N}\) con el objetivo de estimar \(M\). Entonces, ejecutamos otra vez, pero esta vez con \(2^p = c \sqrt{\tilde{M}N}\). De acuerdo con la Ec. (61), pero suponiendo \(2^p = c \sqrt{MN}\) por simplicidad, el error resultante en nuestra segunda estimación de \(M\) es probable que esté acotado por \(\frac{2 \pi}{c} + \frac{\pi^2}{c^2 M}\). En particular, obtenemos una solución exacta, siempre que \(|f - \tilde{f}| < 1\), si tomamos \(c \geq 14\) ya que \(\frac{2 \pi}{c} + \frac{\pi^2}{c^2 M} < \frac{1}{2}\) en ese caso. (Obsérvese que si aplicaciones sucesivamente el algoritmo de Grover y vamos tachamos las soluciones a medida que se encuentran también nos proporcionará un recuento exacto con alta probabilidad en un tiempo en \(\mathcal{O} (\sqrt{M N})\), pero con un consumo enorme de memoria. Ver [3].)

• Finalmente, comentar que si estamos en el caso en el que el número de soluciones es un cuadrado perfecto pequeño, podemos encontrar el valor exacto en un tiempo \(\mathcal{O}(\sqrt{N})\) con una probabilidad de error muy pequeña.

Para más detalles sobre el tema, puede verse [3].

---

Autores:

David Castaño (UMA-SCBI), Raul Fuentes (BSC-CNS), Daniel Talaván (COMPUTAEX), Francisco Matanza (UNICAN)

---

License: Licencia Creative Commons Atribución-CompartirIgual 4.0 Internacional.

This work has been financially supported by the Ministry for Digital Transformation and of Civil Service of the Spanish Government through the QUANTUM ENIA project call - Quantum Spain project, and by the European Union through the Recovery, Transformation and Resilience Plan - NextGenerationEU within the framework of the Digital Spain 2026 Agenda.