May 03, 2024 | 7 min read
1. Introducción#
Este notebook recoge los conceptos básicos para adentrarse en el mundo del QML (Quantum Machine Learning). En primer lugar, se contextualizan los campos en los que se apoya y se explica en qué se basa el QML. Posteriormente, se recogen diferentes conceptos y definiciones que facilitarán la comprensión de los distintos cuadernos teórico-prácticos disponibles.
Para los ejemplos prácticos se han utilizado los siguientes frameworks:
Qibo: es un software de código abierto para trabajar con ordenadores cuánticos a nivel de circuitos, pulsos y algoritmos que cuenta con varias API de aplicaciones específicas. Su objetivo es construir una pila de software (software stack) que facilite el uso de ordenadores cuánticos permitiendo diseñar fácilmente experimentos y aplicaciones y ejecutarlos en ordenadores cuánticos reales y/o simuladores clásicos [31].
1.1. Machine Learning#
El Aprendizaje Automático (en inglés Machine Learning, ML) es uno de los campos más destacados de la Inteligencia Artificial en la actualidad. Se refiere al proceso de construcción de algoritmos que pueden aprender de las observaciones existentes (o conjuntos de datos o datasets) y aprovechar ese aprendizaje para predecir nuevas observaciones o determinar el resultado de nuevas entradas. [21]
Existen cuatro tipos de aprendizaje automático que se clasifican en función de la disponibilidad de las salidas de los ejemplos, es decir, dependerá de si se conoce el valor esperado para cada instancia del problema o no. La Fig. 1 recoge de forma esquemática dicha clasificación.
El primer tipo corresponde al aprendizaje supervisado. En este caso se conoce la salida de todas las instancias del problema, es decir, el conjunto de datos con el que se trabaja tiene registrados los valores a predecir de todos los ejemplos disponibles. Por lo tanto, se le podrá mostrar al algoritmo toda la información necesaria para elaborar su solución. [21]
En el aprendizaje no supervisado sin embargo, los valores de la variable salida son desconocidos, por lo que se utilizan otro tipo de algoritmos para descubrir la estructura de los datos. Se intentan agrupar dichos ejemplos en distintos grupos con características en común. [21]
El aprendizaje semi supervisado es una mezcla de los dos anteriores, en este caso se conoce la salida únicamente para algunos de los ejemplos, en la mayoría de ellos no se disponen de estos valores. Este tipo de aprendizaje está presente en los casos en los que el coste de conocer el valor para la variable salida es muy grande pero el obtener los datos sin esta información conlleva un coste muy bajo. [21]
Por último, el aprendizaje por refuerzo se trata de un tipo distinto a los comentados anteriormente. Son algoritmos que aprenden por si mismos mediante recompensas. No se dispone del valor de salida por lo que no se encuentra dentro del aprendizaje supervisado, pero tampoco se trata de intentar obtener grupos con características comunes por lo que tampoco forma parte del no supervisado. [21]
También es interesante conocer que, dentro del aprendizaje supervisado, los problemas se pueden catalogar como problemas de regresión o clasificación. En los problemas de regresión, el resultado a predecir será un valor numérico y en los problemas de clasificación se pretende predecir una clase, entendiendo por “clase” a una de las categorías arbitrarias según nuestro problema. La Fig. 1 muestra las categorías de los métodos de ML.
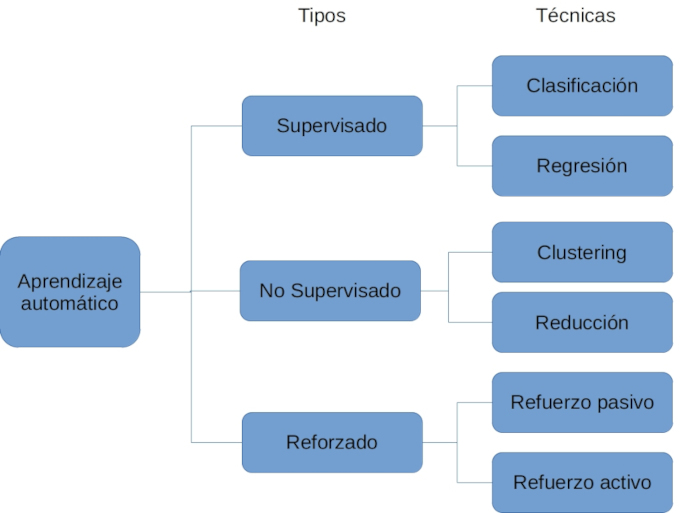
Fig. 1 La categorías de los métodos de ML#
1.2. Quantum Machine Learning#
La tecnología cuántica ha supuesto un cambio de paradigma en el campo de la computación. Surge el aprendizaje automático cuántico (en inglés, Quantum Machine Learning, QML), un campo en evolución. El aprendizaje automático cuántico viene dado por la combinación de técnicas y algoritmos cuánticos con estrategias habituales en aprendizaje automático como se visualizar en la Fig. 2:
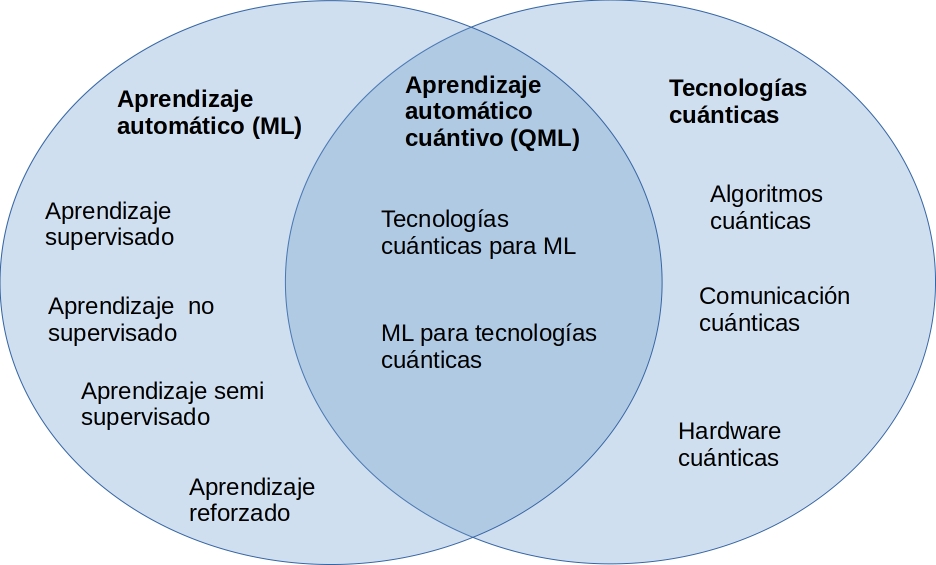
Fig. 2 ML vs QML#
Se puede combinar la computación cuántica con el aprendizaje automático de diversas maneras, obteniendo cuatro áreas de trabajo. Estas corresponden a las que se muestran en la Fig. 3:
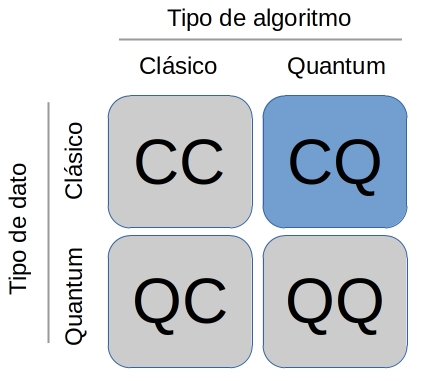
Fig. 3 Áreas de trabajo QML#
CC: Se refiere a procesar datos clásicos con ordenadores clásicos, haciendo uso de algoritmos inspirados en computación cuántica. En otras palabras, hace referencia al machine learning clásico que directamente no tiene una base de quantum, si no que toma prestadas ideas de la física cuántica. [19]
CQ: En este caso, se procesan datos clásicos utilizando algoritmos de quantum machine learning. Será con la tipología que trabajaremos a partir de ahora. En este área se pretende encontrar soluciones más eficaces para problemas típicamente solucionados con ML pero sobre ordenadores cuánticos. [19]
QC: Se trata de un área de investigación, utilizan algoritmos clásicos para tratar datos cuánticos. [19]
QQ: Se podría decir que esta sería la aproximación más “pura”, ya que se realiza un procesamiento de los datos cuánticos y estos datos cuánticos se procesan haciendo uso del aprendizaje automático cuántico. [19]
1.3. Conceptos#
Kernel: El QML puede utilizarse para realizar la evaluación del kernel introduciendo estimaciones de un ordenador cuántico en el método estándar. Aunque el entrenamiento y la inferencia del modelo tendrán que hacerse en el SVM (Support-Vector Machine) estándar, el uso de QSVM (Quantum SVM) podría ayudar a acelerar el proceso. A medida que se amplía el espacio de características, la estimación de las funciones kernel en la computación clásica resulta costosa desde el punto de vista computacional. Las propiedades cuánticas ayudan a crear un espacio de estado cuántico masivo que puede mejorar la evaluación de los kernels [13].
PCA (Principal Component Analysis): Es una técnica de extracción de características donde se combinan las entradas de una manera específica y se pueden eliminar algunas de las variables “menos importantes” manteniendo la parte más significativa de todas las variables. Como valor añadido, tras aplicar técnicas de PCA se obtienen variables independientes entre sí [3].
Función de coste: Trata de definir el error entre el valor estimado y el valor real con el fin de optimizar el algoritmo. En otras palabras, la función de coste cuantifica el error que se ha cometido al predecir los valores deseados.
Optimización: Los problemas de optimización están presentes en muchos campos de estudio e implican encontrar las entradas que darán el mejor resultado posible para un problema dado. Por lo general, encontrar el mejor resultado posible equivale a minimizar la función de coste [2]. Los algoritmos de optimización de inspiración cuántica aprovechan algunas de las ventajas de la computación cuántica en hardware clásico, lo que proporciona más velocidad que en los enfoques tradicionales. Los algoritmos de inspiración cuántica son algoritmos clásicos en los que se puede emular de forma clásica el fenómeno cuántico esencial que proporcionaría el aumento de velocidad.
Gradiente: En matemáticas el gradiente es una generalización de la derivada. La derivada se puede definir solo en funciones de una sola variable, en funciones de varias variables este término se denomina gradiente. Debido a esto, el gradiente es una función de valor vectorial a diferencia de una derivada que toma un valor escalar. Al igual que la derivada, el gradiente representa la pendiente de la recta tangente a la función estudiada, concretamente el gradiente apunta a aquellos puntos de la función con mayor incremento. En el caso de machine learning, resulta de interés el gradiente de la función de coste [26].
Medida (Measurement): El paso final en computación cuántica es la medida de uno o más qubits, después de todo se necesita obtener el resultado de lo que se ha estado calculando cuánticamente. Pese a que este último paso puede parecer una última capa del circuito, no se tiene en cuenta a la hora de calcular la profundidad. La definición de la medida es el problema central de la mecánica cuántica y esta estrechamente relacionada con las amplitudes del estado con el que se está trabajando, ya que el resultado obtenido depende de dichas probabilidades [33].
Función convexa: Una función es convexa en un punto cuando la función cae por encima de la tangente en ese punto [6]. En otras palabras, consideramos que una función es convexa cuando tiene forma de valle, una función de este tipo se visualiza como en la Fig. 4.
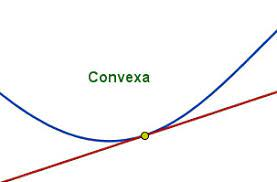
Fig. 4 Visualización función convexa#
Función cóncava: Una función es cóncava en un punto cuando la función cae por debajo de la tangente en ese punto [6]. Dicho de otra manera, este tipo de funciones se asemejan a la forma de una montaña, tal y como se muestra en la Fig. 5.
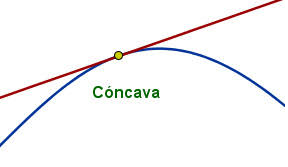
Fig. 5 Visualización función cóncava#
Autores:
Carmen Calvo (SCAYLE), Antoni Alou (PIC), Carlos Hernani (UV), Nahia Iriarte (NASERTIC) y Carlos Luque (IAC)







License: Licencia Creative Commons Atribución-CompartirIgual 4.0 Internacional.
This work has been financially supported by the Ministry for Digital Transformation and of Civil Service of the Spanish Government through the QUANTUM ENIA project call - Quantum Spain project, and by the European Union through the Recovery, Transformation and Resilience Plan - NextGenerationEU within the framework of the Digital Spain 2026 Agenda.

