Ctrl+K

4. Quantum Support Vector Machines (QSVM)

May 03, 2024 | 6 min read

\( \renewcommand{\bra}[1]{\langle #1|} \) \( \renewcommand{\ket}[1]{|#1\rangle} \) \( \renewcommand{\braket}[2]{\langle #1|#2\rangle} \) \( \newcommand{\ketbra}[2]{| #1\rangle \langle #2|} \) \( \renewcommand{\i}{{\color{blue} i}} \) \( \newcommand{\Hil}{{\mathbb H}} \) \( \newcommand{\boldn}{{\bf n}} \) \( \newcommand{\tr}{{\rm tr}}\) \( \newcommand{\bn}{{\bf n}} \)

Consulta la notación que se ha utilizado durante todo el documento en el siguiente enlace.

4. Quantum Support Vector Machines (QSVM)#

En esta sección, se tratarán las máquinas de vectores de soporte o de soporte vectorial (en inglés Support Vector Machines, SVM) tanto en computación clásica como en computación cuántica. En este último caso, la solución es conocida como máquinas de vectores de soporte cuánticos (en su sigla en inglés QSVM). A su vez, se presentarán algunas implementaciones de ambas computaciones.

4.1. Support Vector Machines (SVM)#

Las máquinas de vectores de soporte o de soporte vectorial son un conjunto de modelos de aprendizaje supervisado propuesto por Vladimir Vapnik .atl en 1964 y posteriormente fueron mejorados en diferentes versiones [38], [8]. Los SVMs se pueden aplicar en procesos de clasificación, regresión y detección de valores atípicos (en inglés, outliers).

En clasificación, es conocido como clasificador de vectores de soporte (SVC, en sus siglas en inglés). El SVC construye el hiperplano óptimo que maximiza la distancia entre dos categorías del conjunto de datos para una mejor predicción. Es decir, busca el hiperplano con la mayor distancia de separación entre las dos categorías del conjunto de datos. Esta característica lo diferencia de los modelos de perceptrón, que buscan el hiperplano que distingue las dos categorías del conjunto de datos. Intuitivamente, una buena separación se consigue mediante el hiperplano que tiene la mayor distancia al punto de datos de entrenamiento más cercano de cualquier categoría (llamado margen funcional), ya que, en general, cuanto mayor es el margen, menor es el error de generalización del clasificador [15].

En la Fig. 7 se visualizan tres posibles hiperplanos para separar las dos clases/categorías del conjunto de datos, representadas por puntos negros y blancos. Los ejes \(x_{1}\) y \(x_{2}\) corresponden a las características de cada instancia en el conjunto de datos. El hiperplano H1 no separa adecuadamente las clases del conjunto de datos; el hiperplano H2 las separa con un margen pequeño y, en cambio, el hiperplano H3 las distingue con la distancia óptima. En consecuencia, se genera la frontera de decisión adecuada u óptima para la predicción. En otras palabras, el SVM con el hiperplano H3 distinguirá con mayor probabilidad la clase a la que pertenece un nuevo punto.

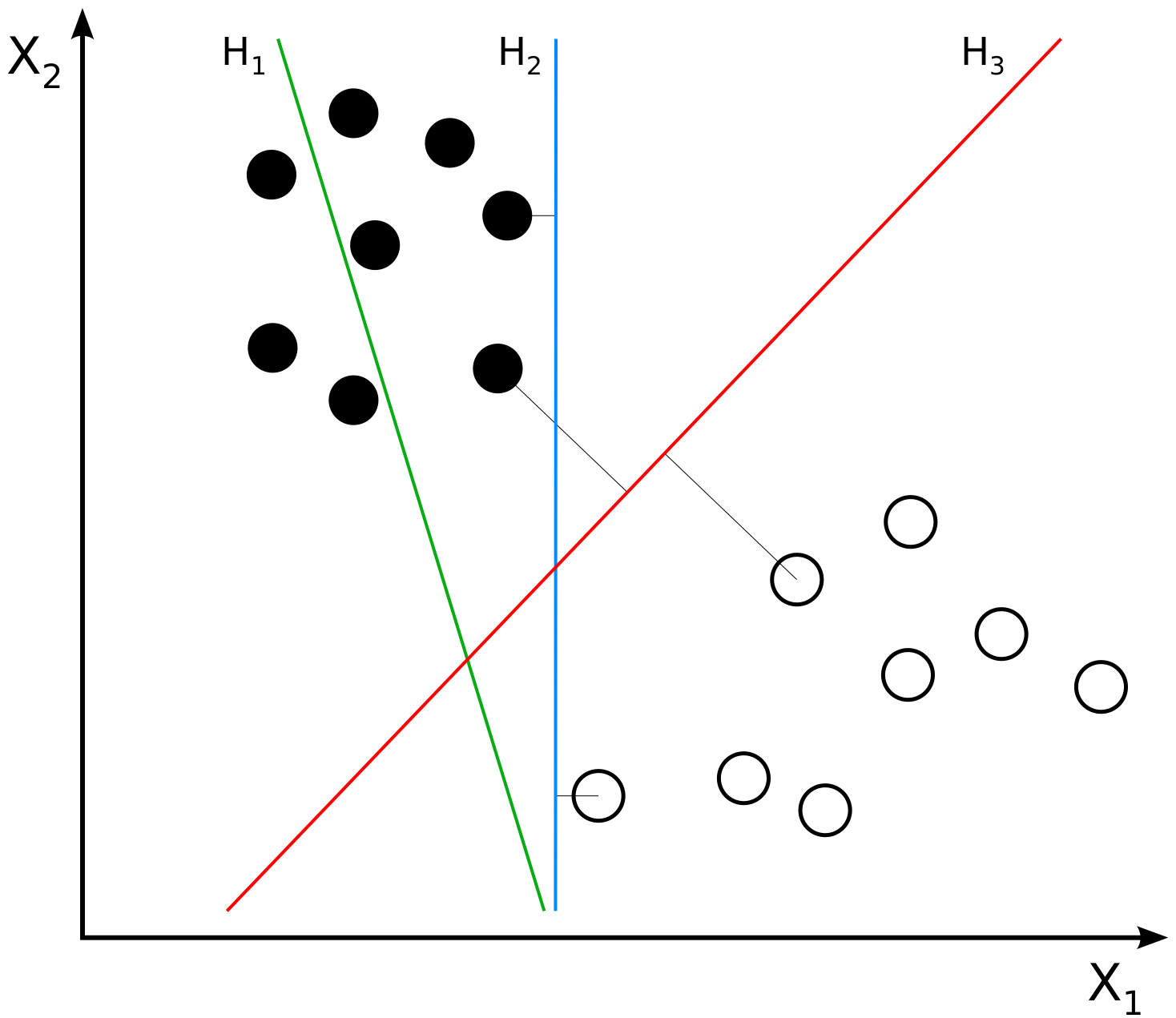
../../_images/Svm_separating_hyperplanes.png

Fig. 7 SVM con distintos hiperplanos#

En general, un conjunto de datos no es linealmente separable y el SVC no encontraría un hiperplano óptimo. En estos casos, se aplica el método del kernel, que permite el mapeo de los datos a otro espacio de características con mayor dimensión, donde sería más sencillo encontrar el hiperplano óptimo. Para más detalle de los métodos kernel, visualice el notebook 5. Quantum Kernels.

4.2. Clasificador de vectores de soporte cuántico#

El clasificador de vectores de soporte cuántico (QSVC, en sus siglas en inglés) es la aplicación del SVC en computación cuántica, como se ilustra en la Fig. 8. Aprovecha la capacidad del SVC para trabajar con métodos kernel, los cuales pueden calcularse de manera eficiente en computación cuántica. De esta manera, se beneficia de la alta dimensionalidad del espacio de Hilbert [16], [37]. Para más detalles de los métodos kernel, visualice el notebook 5. Quantum Kernels.

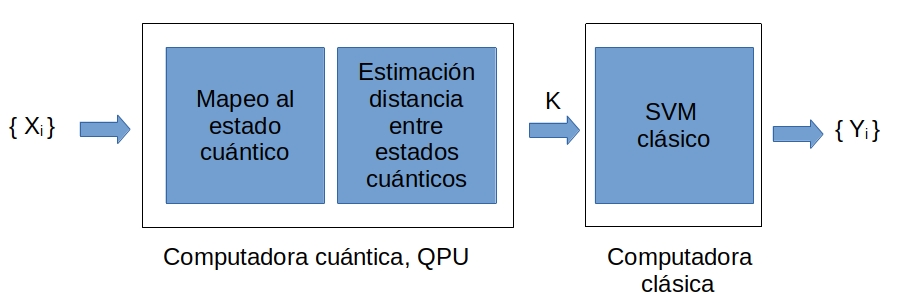
../../_images/qsvm_kernel.jpg

Fig. 8 Flujo de trabajo del QSVC#

El QSVC corresponde en varios pasos como se visualiza en la Fig. 8:

  1. La generación de un kernel cuántico, \(K\):

    1. Mapeo de cada dato clásico, \(\mathbf{x_{i}}\), en un estado cuántico \(\vert \Phi{(\mathbf{x_{i}})} \rangle\). Esto se puede lograr con el circuito cuántico \(\mathcal{U}_{\Phi{(\mathbf{x_{i}})}}\), \(\mathcal{U}_{\Phi{(\mathbf{x_{i}})}} \vert 0^{\otimes N} \rangle = \vert \Phi{(\mathbf{x_{i}})} \rangle\), donde el valor inicial de cada qubit es \(\ket{0}\) y \(N\) es el número de características o qubits.

    2. Obtención de la matriz del kernel, cada elemento de la matriz del kernel se calcula, \(K_{i,j} = |\braket{\Phi(\mathbf{x_{i}})}{\Phi(\mathbf{x_{j}})}|^2 = |\bra{0^{\otimes N}} \mathcal{U}^\dagger_{ \Phi(\mathbf{x_{i}})} \mathcal{U}_{ \Phi{(\mathbf{x_{j}})}} \ket{0^{\otimes N}}|^2 \) donde \(i,j = 0...M\) y \(M\) es el número de vectores de características en el conjunto de datos. \(K_{i,j}\) se interpreta como una medida de similitud o de distancia entre estados cuánticos.

  2. Se aplica la matriz de kernel en el algoritmo de SVC clásico para entrenar y obtener la predicción.

4.2.1. Ejemplo de QSVM en Qibo#

El ejemplo se basa en un tutorial de pennylane [34]. En este, se usará el SVM de la librería scikit-learn, sklearn. La interfaz permite proporcionar kernel adicional en dos formas:

  1. La función que calcula la matriz del kernel.

    • (kernel= nombrefunción)

  2. La matriz del kernel calculada.

    • (kernel=“precomputed”)

En el ejemplo, se aplicará la primera forma, facilitando la función que calcula la matriz del kernel. A su vez, el famoso conjunto de datos, Iris, [11]. Este conjunto de datos, que data de 1936, consta de 150 muestras de cuatro características cada una y da lugar a un problema de clasificación y se utilizará solo las primeras 100 muestras.

Se cargan las librerías necesarias:

import numpy as np 
import matplotlib.pyplot as plt

# librería con SVM
from sklearn import svm

# Carga el conjunto de datos y algunas funciones adicionales
from sklearn.datasets import load_iris
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

# Librería cuántico (Qibo)
import qibo
from qibo import gates
from qibo.models import Circuit

#Uso de backend de numpy en Qibo
qibo.set_backend("numpy")

[Qibo 0.1.12.dev0|INFO|2024-06-11 12:06:45]: Using numpy backend on /CPU:0

Se carga el conjunto de datos, \(X\), se seleccionan las primeras 100 muestras y luego se adaptan los datos aplicando un escalado periódico mediante la codificación a datos cuánticos. Este proceso implica la transformación de los datos a la distribución normal estándar, también conocida como la distribución Z.

A su vez, el conjunto de datos se divide en dos grupos:

  • Entrenamiento

  • Testeo

X, y = load_iris(return_X_y=True)

# Se selecciona solo la dos primeras clases del conjunto 
# de datos debido a que el clasificador es binario
X = X[:100]
y = y[:100]

# Escalar los datos a distribución normal estándar debido a la 
# codificación datos es periódica
scaler = StandardScaler().fit(X)
X_scaled = scaler.transform(X)

# Escalar las etiquetas a -1 y 1 debido que es importante para SVM
y_scaled = 2 * (y - 0.5)

# Se divide en entrenamiento y testeo
X_train, X_test, y_train, y_test = train_test_split(X_scaled, y_scaled)

La codificación de los datos clásicos a estados cuánticos se llevará a cabo mediante la codificación en ángulo, utilizando puertas de rotación. Para obtener más detalles sobre la codificación cuántica, consulte el notebook 2. Feature encoding. En el ejemplo, se aplica la puerta de rotación en el eje Y para codificar los datos clásicos en estados cuánticos. Esta puerta no introduce componentes imaginarias.

Dado que cada vector de características consta de cuatro características, se necesitarán cuatro qubits para codificar los estados cuánticos, por lo tanto, \(N = 4\).

Para estimar la distancia entre dos estados cuánticos, es decir, el producto escalar, se aplica el test invertido o quantum kernel estimation [16]. Para obtener más detalles sobre los kernels, consulte el notebook 5. Quantum Kernels. En el ejemplo, el circuito cuántico representa el cálculo de la distancia entre dos estados cuánticos como \(K_{i,j} = |\braket{\Phi(\mathbf{x_{i}})}{\Phi(\mathbf{x_{j}})}|^2 = |\bra{0^{\otimes N}} \mathcal{U}^\dagger_{ \Phi(\mathbf{x_{i}})} \mathcal{U}_{ \Phi{(\mathbf{x_{j}})}} \ket{0^{\otimes N}}|^2 \). El estado cuántico resultante \(\ket{\phi}\) se mide con respecto al estado computacional \(\ket{0^{\otimes N}}\), y el resultado es la probabilidad \(|\braket {0^{\otimes N}} {\phi}|^2\) de observar la base computacional \(\ket{0^{\otimes N}}\) del estado cuántico actual \(\ket{\phi}\). Este cálculo se basa en las reglas de Born [1].

Para obtener las probabilidades en la base computacional \(\ket{0^{\otimes N}}\) en una computadora cuántica, el circuito cuántico debe ser ejecutado varias veces o shots. Según el artículo Supervised learning with quantum-enhanced feature spaces [16], el circuito debería ejecutarse 50000 veces. En el ejemplo, se usa 8000 por limitación del computador cuántico.

# kernel cuántico
def distancia_circuit(x,y):
    
    # cuatro cúbits: cuatro características
    n_qubits = len(X_train[0]) 
    n_shots = 8000

    # Create an empty circuit
    circuit = Circuit(n_qubits)

    # Codificación cuántica en puertas RY 
    for pos in range(n_qubits):
        circuit.add(gates.RY(pos, y[pos]))
        circuit.add(gates.RY(pos, x[pos]).dagger())
        circuit.add(gates.M(pos))

    # ejecución del circuito n veces (n_shots)
    result = circuit.execute(nshots=n_shots)
    # Devuelve las probabilidades analíticas
    return result.probabilities()
       
# Se devuelve el probabilidad del base computacional "0000"
kernel = lambda x1, x2: distancia_circuit(x1, x2)[0]

Se verifica que el kernel cuántico funciona correctamente con el vector de características \(\mathbf{x}\) consigo mismo. El resultado debería ser 1, es decir, la probabilidad del estado inicial \(\ket{\phi}{\text{inicial}} = \ket{0^N}\) es igual a la probabilidad del estado final \(\ket{\phi}{\text{final}} = \ket{0^N}\).

x = np.array([np.pi/2,np.pi/2,np.pi/2,np.pi/2])
kernel(x,x)

1.0

Se define una función que calcula una matriz de kernel para los vectores de características en dos conjuntos de datos diferentes \(A, B\). Si \(A=B\), la matriz del kernel es conocida como la matriz de Gram [5].

def kernel_matrix(A, B):
    return np.array([[kernel(a, b) for b in B] for a in A])

Para el entrenamiento, se inicializa el clasificador SVC con la matriz del kernel cuántico.

# Inicialización
qsvm = svm.SVC(kernel=kernel_matrix)

print("Entrenando...")
qsvm = qsvm.fit(X_train, y_train)

print("Entrenado!")

Entrenando...
Entrenado!

Se calcula la precisión en la clasificación con el conjunto de datos de test.

#test
print("Precisión con test...")

predictions = qsvm.predict(X_test)
accuracy_score(predictions, y_test)

Precisión con test...

1.0

Se compara el resultado con un SVM clásico con kernel lineal

modelclasico = svm.SVC(kernel="linear")
modelclasico.fit(X_train, y_train)

print("Precisión con test...")

predictions = modelclasico.predict(X_test)
accuracy_score(predictions, y_test)

Precisión con test...

1.0

Nota (Anexo notación)

Para que la comprensión de los notebooks sea mejor se ha unificado la notación utilizada en los mismos. Para diferenciar un vector de un valor único se hará uso de la negrita. De manera que \(\mathbf{x}\) corresponde a un vector y \(z\) será una variable de una única componente.

Si se quiere hacer referencia a dos vectores distintos pero que pertenecen al mismo dataset se utilizará un subíndice, es decir, \(\mathbf{x_i}\) hará referencia al i-ésimo vector del dataset. Si se quiere referenciar una característica concreta del vector se añadirá un nuevo subíndice, de manera que \(\mathbf{x_{i_j}}\) hará referencia a la j-ésima variable del i-ésimo vector.

Autores:

Carmen Calvo (SCAYLE), Antoni Alou (PIC), Carlos Hernani (UV), Nahia Iriarte (NASERTIC) y Carlos Luque (IAC)

../../_images/LOGO-SCAILE.png ../../_images/Logo_pic.png ../../_images/Logo_UV.jpg ../../_images/Logo_Nasertic.png ../../_images/Logo_IAC.jpg
https://quantumspain-project.es/wp-content/uploads/2022/11/Logo_QS_EspanaDigital.png
Licencia Creative Commons

License: Licencia Creative Commons Atribución-CompartirIgual 4.0 Internacional.

This work has been financially supported by the Ministry for Digital Transformation and of Civil Service of the Spanish Government through the QUANTUM ENIA project call - Quantum Spain project, and by the European Union through the Recovery, Transformation and Resilience Plan - NextGenerationEU within the framework of the Digital Spain 2026 Agenda.

Contents