May 06, 2024 | 6 min read
Introducción al Algoritmo VQE#
Show code cell source
# Librerías generales
import numpy as np
from collections import defaultdict
from functools import reduce
from itertools import product
import random
import scipy
import matplotlib.pyplot as plt
# Librerías Qibo
import qibo
from qibo import models, gates, hamiltonians
from qibo import matrices as m
# Librerías Qiskit
import qiskit
from qiskit import IBMQ, QuantumCircuit, QuantumRegister, ClassicalRegister, Aer, execute, transpile
from qiskit.visualization import plot_bloch_multivector
from qiskit.algorithms.optimizers import COBYLA, SPSA, POWELL
from qiskit.primitives import Estimator
from qiskit.algorithms.minimum_eigensolvers import VQE
from qiskit.utils import QuantumInstance, algorithm_globals
from qiskit.opflow import X, Z, I, Y
from qiskit.circuit.library import TwoLocal
from qiskit.tools.parallel import parallel_map
random.seed()
qibo.set_backend("numpy")
%matplotlib inline
A lo largo de este documento vamos a explicar y ejemplificar el funcionamiento del algoritmo VQE. Para ello haremos uso de la librería de software libre Qibo. Puede encontrar más información sobre el proceso de instalación aquí. Así mismo, en la sección La molécula de \text{H}_2 de este documento hacemos uso de la librería OpenFermion, desarrollada por Google. Puede encontrar aquí instrucciones para su instalación. También en esta sección hacemos uso de la librería de química computacional PySCF. Puede consultar las instrucciones de instalación aquí.
Introducción al Algoritmo#
El algoritmo VQE (Variational Quantum Eigensolver) es un algoritmo que busca obtener el autovalor más pequeño de un operador. Se originó en el campo de la química computacional [17], donde se propuso para encontrar el estado fundamental de moléculas, aunque tiene aplicaciones en muchos otros campos [22].
Se trata de un algoritmo híbrido, pues combina computación cuántica y clásica. Utiliza un circuito cuántico parametrizado para generar estados cuánticos y posteriormente medir el valor esperado del operador. Este valor esperado se utilizará como función de coste para un optimizador clásico, que se encargará de ir variando los parámetros del circuito y devolviéndolos al sistema cuántico de forma iterativa hasta encontrar el autovalor mínimo.
El circuito parametrizado, conocido como ansatz, será equivalente a un operador unitario que llamaremos \(U(\boldsymbol{\theta})\), en el que \(\boldsymbol{\theta}\) es un vector que contiene todos los parámetros del circuito. Este actuará sobre nuestros qubits inicialidados en el estado que más nos interese según la aplicación. Esto generará un estado parametrizado \(|\Psi(\boldsymbol{\theta}) \rangle\). Esto nos permite explorar un subespacio del espacio de Hilbert. En este sentido, la elección del ansatz y el estado incial es crucial, ya que de esto depende en gran medida si conseguiremos encontrar el valor mínimo o no.
Sobre ese estado parametrizado podremos medir el valor esperado del operador problema \(\mathcal{H}\). Este valor será, al igual que el estado, dependiente de los parámetros del ansatz, y lo denotamos por \(E(\boldsymbol{\theta})\). Utilizaremos este valor como función de coste para un optimizador clásico, de manera que tras un número suficiente de iteraciones conseguiremos una muy buena aproximación del autovalor más pequeño de nuestro operador \(E_{G}\).
El funcionamiento del circuito sería algo así:
Fig. 1 Diagrama de flujo del algoritmo VQE. En primer lugar tenemos un problema caracterizado por un operador \(\mathcal{H}\). Codificamos ese problema en un circuito cuántico con puertas parametrizadas. De ahí realizamos un proceso de optimización clásico. Si no converge, devolvemos los datos al circuito cuántico. Si converge, tenemos el resultado \(E_G\).#
Programando el Algoritmo VQE#
Vamos a ver el funcionamiento de este algoritmo para un caso trivial, programando “manualmente” siguiendo el método que se emplea en la referencia [26]. Estas funciones son bastante ineficientes y no pueden competir con las funciones built-in en librerías como Qibo, Qiskit o Pennylane, pero nos ayudan a ver cada parte de forma individual. En las siguientes secciones analizaremos casos prácticos haciendo uso de estas funciones mejor optimizadas.
El problema a resolver es encontrar el autovalor más pequeño de la siguiente matriz \( 4 \times 4\):
Vamos a dejarla diagonalizada también con Python, para asegurarnos de que obtenemos los autovalores correctos:
op = np.array([[2.5,-1,-0.5,0],[-1,2.5,0,0.5],[-0.5,0,2.5,1],[0,0.5,1,2.5]], dtype=complex)
eigvals, eigvecs = scipy.linalg.eig(op)
print("Autovalores:", np.sort(np.real(eigvals)))
print("Autovalor mínimo:", np.real(np.round(min(eigvals))))
Autovalores: [1. 2. 3. 4.]
Autovalor mínimo: 1.0
Empezamos por definir las matrices de Pauli, ya que son los principales operadores que se utilizan en circuitería cuántica. Todo operador hermítico de dimensión \(2^n\) (entre los que se incluye nuestro operador \(\mathcal{H}\)) puede descomponerse en productos tensoriales de matrices de Pauli. Estas, al ser hermíticas y unitarias, nos permiten tanto descomponer operadores como construir circuitos cuánticos.
PAULIS = {
"I": np.eye(2, dtype=complex),
"X": np.array([[0,1],[1,0]], dtype=complex),
"Y": np.array([[0,-1j],[1j,0]], dtype=complex),
"Z": np.array([[1,0],[0,-1]], dtype=complex)
}
Definimos la función pauli_decomposition(H), que toma nuestro operador matricial \(\mathcal{H}\) y lo convierte en una cadena de matrices de Pauli.
def pauli_decomposition(H):
n = int(np.log2(len(H)))
dims = 2**n
if H.shape != (dims,dims):
raise ValueError("La matriz debe tener dimensiones 2^n x 2^n")
basis_key = ["".join(k) for k in product(PAULIS.keys(), repeat = n)]
components = defaultdict(int)
for i, val in enumerate(product(PAULIS.values(), repeat=n)):
basis_mat = reduce(np.kron, val)
coeff = H.reshape(-1).dot(basis_mat.reshape(-1)) / dims
coeff = np.real_if_close(coeff).item()
if not np.allclose(coeff,0):
components[basis_key[i]] = coeff
return components
components = pauli_decomposition(op)
components
defaultdict(int, {'II': 2.5, 'XZ': -0.5, 'ZX': -1.0})
Si volvemos a sumar nuestras componentes, vemos que se recupera nuestra matriz original \(\mathcal{H}\).
restr = components['II']*np.kron(PAULIS["I"],PAULIS["I"]) + components['XZ']*np.kron(PAULIS["X"],PAULIS["Z"]) + components['ZX']*np.kron(PAULIS["Z"],PAULIS["X"])
print(restr)
if restr.all() == op.all(): print("\n Las dos matrices son iguales.")
[[ 2.5+0.j -1. +0.j -0.5+0.j 0. +0.j]
[-1. +0.j 2.5+0.j 0. +0.j 0.5+0.j]
[-0.5+0.j 0. +0.j 2.5+0.j 1. +0.j]
[ 0. +0.j 0.5+0.j 1. +0.j 2.5+0.j]]
Las dos matrices son iguales.
Definimos también la función ansatz, que, tomando un circuito cuántico y un conjunto de parámetros, nos implementa el estado \(|\psi (\boldsymbol{\theta})\rangle\) como un conjunto de operadores parametrizados.
def ansatz(circuit, nqubits, thetas, rounds=3):
for r in range(rounds):
for i in range(nqubits):
offset = r*nqubits*2 + i*2
circuit.add(gates.RY(i, thetas[offset]))
circuit.add(gates.RZ(i, thetas[offset+1]))
if i > 0 and r < rounds - 1:
circuit.add(gates.CNOT(i-1, i))
return circuit
def ansatz(qc, qr, thetas, rounds=3):
for r in range(rounds):
for i in range(len(qr)):
offset = r*len(qr)*2 + i*2
qc.ry(thetas[offset], qr[i])
qc.rz(thetas[offset+1], qr[i])
if i > 0 and r < rounds - 1:
qc.cx(qr[i-1], qr[i])
return qc
Veamos un ejemplo de ansatz que generaría este circuito si consideramos tres qubits:
nqubits = 3
nrounds = 4
qc = models.circuit.Circuit(nqubits)
angles = np.random.rand(2*nqubits*nrounds)
qc = ansatz(qc, nqubits=nqubits, thetas=angles, rounds=nrounds)
print(qc.draw())
nqubits = 3
nrounds = 4
qr = QuantumRegister(nqubits)
qc = QuantumCircuit(qr)
angles = np.random.rand(2*nqubits*nrounds)
qc = ansatz(qc, qr, thetas=angles, rounds=nrounds)
qc.draw('mpl')
q0: ─RY─RZ─o─────────RY─RZ─o─────────RY─RZ─o─────────RY─RZ─
q1: ─RY─RZ─X───────o─RY─RZ─X───────o─RY─RZ─X───────o─RY─RZ─
q2: ─────────RY─RZ─X─────────RY─RZ─X─────────RY─RZ─X─RY─RZ─
En este caso concreto, tenemos puertas parametrizadas \(R_Y\) y \(R_Z\), cuyos ángulos de rotación son los parámetros \(\boldsymbol{\theta}\) que vamos a ir modificando hasta llegar al autovalor mínimo. Por supuesto, podríamos haber utilizado también puertas \(R_X\) o cualquier puerta que rotase los qubits en torno a un eje arbitrario.
Para entrelazar qubits hemos utilizado puertas \(CNOT\), aunque también se suelen usar \(CZ\).
Con todas estas herramientas, podemos definir la función matrix_decomposition_circuits, que toma nuestro operador \(\mathcal{H}\) y, utilizando pauli_decomposition, lo convierte en una suma de cadenas de Pauli. Con esto define tantos circuitos cuánticos como cadenas tengamos, añadiendo a cada uno de ellos nuestro ansatz empleando ansatz (la función add_ansatz(qc, qr) se define con ella).
Después, dependiendo de como sean las cadenas de Pauli, añade los medidores que correspondan según la base (por ejemplo, si estamos midiendo en la dirección \(Y\), debemos rotar nuestro qubit utilizando \(H\) y \(S^\dagger\)).
def matrix_decomposition_circuits(H, add_ansatz):
from qibo import models, gates
# Definimos variables y comprobamos las dimensiones del Hamiltoniano
n = int(np.log2(len(H)))
dims = 2**n
if H.shape != (dims,dims):
raise ValueError("La matriz debe tener dimensiones 2^n x 2^n")
# Descomponemos el Hamiltoniano en cadenas de Pauli
components = pauli_decomposition(H)
circuits = {}
for (paulistring, weight) in components.items():
paulis = list(enumerate(reversed(paulistring)))
qc = models.Circuit(n)
# No hacemos nada si todas las Pauli son I, utilizamos este circuito vacío que medirá el estado "0" (autovalor 1) en todos los caso
if all(x[1] == "I" for x in paulis):
qc.add(gates.M(qc.nqubits-1))
circuits[paulistring] = (qc, weight)
continue
# Al resto de posibles circuitos sí les añadimos el ansatz
add_ansatz(qc,n)
# Hacemos las transformaciones sobre un solo qubit
for idx, letter in paulis:
if letter == "X":
qc.add(gates.H(idx))
elif letter == "Y":
qc.add(gates.H(idx))
qc.add(gates.S(idx).dagger())
# Añadimos las puertas multiqubit
for idx, (first, second) in enumerate(zip(paulis, paulis[1:])):
if second[1] == "I":
qc.add(gates.SWAP(first[0], second[0]))
elif first[1] != "I":
paulis[idx+1] = (paulis[idx+1][0], paulis[idx][1])
qc.add(gates.CNOT(first[0],second[0]))
# Medimos sobre el último qubit
qc.add(gates.M(qc.nqubits-1))
circuits[paulistring] = (qc, weight)
return circuits
def matrix_decomposition_circuits(H, add_ansatz):
# Definimos variables y comprobamos las dimensiones del Hamiltoniano
n = int(np.log2(len(H)))
dims = 2**n
if H.shape != (dims,dims):
raise ValueError("La matriz debe tener dimensiones 2^n x 2^n")
components = pauli_decomposition(H)
circuits = {}
for (paulistring, weight) in components.items():
paulis = list(enumerate(reversed(paulistring)))
qr = QuantumRegister(n, "qr")
cr = ClassicalRegister(1, "cr")
qc = QuantumCircuit(qr, cr)
add_ansatz(qc,qr)
# No hacemos nada si todas las Pauli son I
if all(x[1] == "I" for x in paulis):
# utilizamos este circuito vacío que medirá el estado "0" (autovalor 1) en todos los casos
circuits[paulistring] = (qc, weight)
continue
# Hacmos las transformaciones sobre un solo qubit
for idx, letter in paulis:
if letter == "X":
qc.h(qr[idx])
elif letter == "Y":
qc.h(qr[idx])
qc.sdg(qr[idx])
# Añadimos las puertas multiqubit
for idx, (first, second) in enumerate(zip(paulis, paulis[1:])):
if second[1] == "I":
qc.swap(first[0], second[0])
elif first[1] != "I":
paulis[idx+1] = (paulis[idx+1][0], paulis[idx][1])
qc.cx(first[0],second[0])
# Medimos sobre el último qubit
qc.measure(qr[-1], cr[0])
circuits[paulistring] = (qc, weight)
return circuits
Definimos ahora la función run_circuit, que lo que hace es ejecutar el circuito utilizando el backend que hayamos especificado y nos devuelve el valor esperado de la medida del circuito.
def run_circuit(circuit, shots=10000):
result = circuit.execute(nshots=shots)
counts = result.frequencies(binary=True)
return ((counts["0"] if "0" in counts.keys() else 0) - (counts["1"] if "1" in counts.keys() else 0))/shots
def run_circuit(circuit, backend, shots=10000):
result = execute(circuit, backend, shots=shots).result()
counts = result.get_counts()
return ((counts["0"] if "0" in counts.keys() else 0) - (counts["1"] if "1" in counts.keys() else 0))/shots
Definimos ahora expectation, que ejecuta los circuitos generados por matrix_decomposition_circuits utilizando run_circuit y suma sus resultados con los coeficientes de la descomposición, devolviendo el valor esperado del operador problema.
def expectation(H, rounds, thetas):
circuits = matrix_decomposition_circuits(H, lambda qc,n: ansatz(qc, n, thetas, rounds))
return sum(map(lambda key: run_circuit(circuits[key][0])*circuits[key][1], circuits.keys()))
def expectation(H, rounds, thetas):
backend = Aer.get_backend('statevector_simulator')
circuits = matrix_decomposition_circuits(H, lambda qc,qr: ansatz(qc, qr, thetas, rounds))
return sum(map(lambda key: run_circuit(circuits[key][0], backend)*circuits[key][1], circuits.keys()))
Ahora definimos nuestro optimizador clásico. Vamos a utilizar un optimizador numérico conocido como SPSA (Simultaneous Perturbation Stochastic Approximation) [3]. Lo programamos a continuación para ver cómo funciona pero, de nuevo, en adelante utilizaremos optimizadores que podemos encontrar en las librerías.
class SPSA:
def __init__(self, a, c, A, alpha, gamma, H, loss_function):
# Inicializamos parámetros de ganancia y factores de decaímiento
self.a = a
self.c = c
self.A = A
self.alpha = alpha
self.gamma = gamma
self.loss_function = loss_function
# Contador
self.t = 0
def step(self, current_estimate):
# Obtenemos los valores actuales para las secuencias de ganancia
a_t = self.a / (self.t + 1 + self.A)**self.alpha
c_t = self.c / (self.t + 1)**self.gamma
# Vector de perturbaciones aleatorias de la distribución de Bernoulli
delta = np.random.randint(0, 2, np.array(current_estimate).shape) * 2 - 1
# Medimos la función de pérdida en las perturbaciones
loss_plus = self.loss_function(current_estimate + delta * c_t)
loss_minus = self.loss_function(current_estimate - delta * c_t)
# Estimación del gradiente
g_t = (loss_plus - loss_minus) / (2.0 * delta * c_t)
# Actualizamos la estimación del parámetro
current_estimate = current_estimate - a_t * g_t
# Incrementamos el contador
self.t +=1
return current_estimate
Y ya, con un optimizador clásico y un operador cuántico, podemos definir nuestro algoritmo VQE, utilizando la función expectation como función de pérdida del optimizador (implementando aquí toda la circuitería cuántica).
def vqe(H, rounds, max_iter, thetas=None, save_steps = None):
cnt_qubits = int(np.log2(len(H)))
if thetas is None:
thetas = list(map(lambda x: random.random(), [0] * ((1+rounds)*cnt_qubits*2)))
# Creamos la clase del optimizador
optimizer = SPSA(a = 0.9, c = 1.0, A = max_iter/10, alpha = 0.602, gamma = 0.101, H = H, loss_function = lambda t_thetas: expectation(H, rounds, t_thetas))
# Loop principal
for i in range(max_iter):
thetas = optimizer.step(thetas)
if save_steps is not None and i % save_steps == 0:
yield (i, thetas, expectation(H, rounds, thetas))
return (thetas, expectation(H, rounds, thetas))
Y con todo este código podemos meter la matriz que diagonalizamos antes a mano y comprobar que, efectivamente, el autovalor más bajo que obtenemos es \(E_G \simeq 1\).
H = op
result = None
step_size = 3
result_energy = []
for step in vqe(H, rounds=3, max_iter=1002, save_steps = step_size):
result_energy.append(step[2])
print('Paso {step}. Valor actual de la función de coste: {ev: .3f}'.format(step=step[0], ev = step[2]))
result = step
print('Los parámetros óptimos para este circuito son: [\n'
+ "".join(["\t"+str(round(t,3))
+",\n" if i%3 == 2 else "\t"+str(round(t,3))
+",\t" for i, t in enumerate(result[1])])+"]")
print('El valor del autovalor mínimo es: {ev: .3f}'.format(ev=result[2]))
Paso 0. Valor actual de la función de coste: 2.766
Paso 3. Valor actual de la función de coste: 2.763
Paso 6. Valor actual de la función de coste: 2.751
Paso 9. Valor actual de la función de coste: 2.679
Paso 12. Valor actual de la función de coste: 2.680
Paso 15. Valor actual de la función de coste: 2.643
Paso 18. Valor actual de la función de coste: 2.599
Paso 21. Valor actual de la función de coste: 2.534
Paso 24. Valor actual de la función de coste: 2.460
Paso 27. Valor actual de la función de coste: 2.434
Paso 30. Valor actual de la función de coste: 2.444
Paso 33. Valor actual de la función de coste: 2.409
Paso 36. Valor actual de la función de coste: 2.442
Paso 39. Valor actual de la función de coste: 2.455
Paso 42. Valor actual de la función de coste: 2.479
Paso 45. Valor actual de la función de coste: 2.440
Paso 48. Valor actual de la función de coste: 2.473
Paso 51. Valor actual de la función de coste: 2.466
Paso 54. Valor actual de la función de coste: 2.375
Paso 57. Valor actual de la función de coste: 2.400
Paso 60. Valor actual de la función de coste: 2.402
Paso 63. Valor actual de la función de coste: 2.385
Paso 66. Valor actual de la función de coste: 2.352
Paso 69. Valor actual de la función de coste: 2.267
Paso 72. Valor actual de la función de coste: 2.287
Paso 75. Valor actual de la función de coste: 2.325
Paso 78. Valor actual de la función de coste: 2.319
Paso 81. Valor actual de la función de coste: 2.249
Paso 84. Valor actual de la función de coste: 2.225
Paso 87. Valor actual de la función de coste: 2.236
Paso 90. Valor actual de la función de coste: 2.224
Paso 93. Valor actual de la función de coste: 2.161
Paso 96. Valor actual de la función de coste: 2.161
Paso 99. Valor actual de la función de coste: 2.171
Paso 102. Valor actual de la función de coste: 2.182
Paso 105. Valor actual de la función de coste: 2.165
Paso 108. Valor actual de la función de coste: 2.060
Paso 111. Valor actual de la función de coste: 2.053
Paso 114. Valor actual de la función de coste: 2.068
Paso 117. Valor actual de la función de coste: 2.059
Paso 120. Valor actual de la función de coste: 2.042
Paso 123. Valor actual de la función de coste: 1.982
Paso 126. Valor actual de la función de coste: 1.988
Paso 129. Valor actual de la función de coste: 1.982
Paso 132. Valor actual de la función de coste: 1.967
Paso 135. Valor actual de la función de coste: 1.943
Paso 138. Valor actual de la función de coste: 1.935
Paso 141. Valor actual de la función de coste: 1.939
Paso 144. Valor actual de la función de coste: 1.930
Paso 147. Valor actual de la función de coste: 1.885
Paso 150. Valor actual de la función de coste: 1.868
Paso 153. Valor actual de la función de coste: 1.854
Paso 156. Valor actual de la función de coste: 1.819
Paso 159. Valor actual de la función de coste: 1.817
Paso 162. Valor actual de la función de coste: 1.818
Paso 165. Valor actual de la función de coste: 1.806
Paso 168. Valor actual de la función de coste: 1.814
Paso 171. Valor actual de la función de coste: 1.812
Paso 174. Valor actual de la función de coste: 1.758
Paso 177. Valor actual de la función de coste: 1.754
Paso 180. Valor actual de la función de coste: 1.742
Paso 183. Valor actual de la función de coste: 1.746
Paso 186. Valor actual de la función de coste: 1.778
Paso 189. Valor actual de la función de coste: 1.775
Paso 192. Valor actual de la función de coste: 1.761
Paso 195. Valor actual de la función de coste: 1.747
Paso 198. Valor actual de la función de coste: 1.726
Paso 201. Valor actual de la función de coste: 1.733
Paso 204. Valor actual de la función de coste: 1.692
Paso 207. Valor actual de la función de coste: 1.653
Paso 210. Valor actual de la función de coste: 1.640
Paso 213. Valor actual de la función de coste: 1.623
Paso 216. Valor actual de la función de coste: 1.566
Paso 219. Valor actual de la función de coste: 1.507
Paso 222. Valor actual de la función de coste: 1.463
Paso 225. Valor actual de la función de coste: 1.457
Paso 228. Valor actual de la función de coste: 1.434
Paso 231. Valor actual de la función de coste: 1.407
Paso 234. Valor actual de la función de coste: 1.403
Paso 237. Valor actual de la función de coste: 1.388
Paso 240. Valor actual de la función de coste: 1.380
Paso 243. Valor actual de la función de coste: 1.368
Paso 246. Valor actual de la función de coste: 1.347
Paso 249. Valor actual de la función de coste: 1.327
Paso 252. Valor actual de la función de coste: 1.306
Paso 255. Valor actual de la función de coste: 1.281
Paso 258. Valor actual de la función de coste: 1.278
Paso 261. Valor actual de la función de coste: 1.271
Paso 264. Valor actual de la función de coste: 1.258
Paso 267. Valor actual de la función de coste: 1.276
Paso 270. Valor actual de la función de coste: 1.254
Paso 273. Valor actual de la función de coste: 1.243
Paso 276. Valor actual de la función de coste: 1.252
Paso 279. Valor actual de la función de coste: 1.241
Paso 282. Valor actual de la función de coste: 1.235
Paso 285. Valor actual de la función de coste: 1.207
Paso 288. Valor actual de la función de coste: 1.183
Paso 291. Valor actual de la función de coste: 1.183
Paso 294. Valor actual de la función de coste: 1.185
Paso 297. Valor actual de la función de coste: 1.149
Paso 300. Valor actual de la función de coste: 1.169
Paso 303. Valor actual de la función de coste: 1.177
Paso 306. Valor actual de la función de coste: 1.173
Paso 309. Valor actual de la función de coste: 1.168
Paso 312. Valor actual de la función de coste: 1.162
Paso 315. Valor actual de la función de coste: 1.162
Paso 318. Valor actual de la función de coste: 1.173
Paso 321. Valor actual de la función de coste: 1.150
Paso 324. Valor actual de la función de coste: 1.150
Paso 327. Valor actual de la función de coste: 1.136
Paso 330. Valor actual de la función de coste: 1.130
Paso 333. Valor actual de la función de coste: 1.134
Paso 336. Valor actual de la función de coste: 1.129
Paso 339. Valor actual de la función de coste: 1.138
Paso 342. Valor actual de la función de coste: 1.143
Paso 345. Valor actual de la función de coste: 1.139
Paso 348. Valor actual de la función de coste: 1.146
Paso 351. Valor actual de la función de coste: 1.133
Paso 354. Valor actual de la función de coste: 1.139
Paso 357. Valor actual de la función de coste: 1.139
Paso 360. Valor actual de la función de coste: 1.130
Paso 363. Valor actual de la función de coste: 1.130
Paso 366. Valor actual de la función de coste: 1.126
Paso 369. Valor actual de la función de coste: 1.134
Paso 372. Valor actual de la función de coste: 1.117
Paso 375. Valor actual de la función de coste: 1.123
Paso 378. Valor actual de la función de coste: 1.113
Paso 381. Valor actual de la función de coste: 1.111
Paso 384. Valor actual de la función de coste: 1.099
Paso 387. Valor actual de la función de coste: 1.099
Paso 390. Valor actual de la función de coste: 1.091
Paso 393. Valor actual de la función de coste: 1.098
Paso 396. Valor actual de la función de coste: 1.085
Paso 399. Valor actual de la función de coste: 1.079
Paso 402. Valor actual de la función de coste: 1.068
Paso 405. Valor actual de la función de coste: 1.064
Paso 408. Valor actual de la función de coste: 1.060
Paso 411. Valor actual de la función de coste: 1.047
Paso 414. Valor actual de la función de coste: 1.053
Paso 417. Valor actual de la función de coste: 1.042
Paso 420. Valor actual de la función de coste: 1.032
Paso 423. Valor actual de la función de coste: 1.032
Paso 426. Valor actual de la función de coste: 1.037
Paso 429. Valor actual de la función de coste: 1.032
Paso 432. Valor actual de la función de coste: 1.041
Paso 435. Valor actual de la función de coste: 1.032
Paso 438. Valor actual de la función de coste: 1.041
Paso 441. Valor actual de la función de coste: 1.043
Paso 444. Valor actual de la función de coste: 1.029
Paso 447. Valor actual de la función de coste: 1.029
Paso 450. Valor actual de la función de coste: 1.035
Paso 453. Valor actual de la función de coste: 1.026
Paso 456. Valor actual de la función de coste: 1.021
Paso 459. Valor actual de la función de coste: 1.020
Paso 462. Valor actual de la función de coste: 1.017
Paso 465. Valor actual de la función de coste: 1.014
Paso 468. Valor actual de la función de coste: 1.015
Paso 471. Valor actual de la función de coste: 1.008
Paso 474. Valor actual de la función de coste: 1.011
Paso 477. Valor actual de la función de coste: 1.010
Paso 480. Valor actual de la función de coste: 1.013
Paso 483. Valor actual de la función de coste: 1.019
Paso 486. Valor actual de la función de coste: 1.018
Paso 489. Valor actual de la función de coste: 1.019
Paso 492. Valor actual de la función de coste: 1.018
Paso 495. Valor actual de la función de coste: 1.016
Paso 498. Valor actual de la función de coste: 1.020
Paso 501. Valor actual de la función de coste: 1.009
Paso 504. Valor actual de la función de coste: 1.012
Paso 507. Valor actual de la función de coste: 1.010
Paso 510. Valor actual de la función de coste: 1.008
Paso 513. Valor actual de la función de coste: 1.012
Paso 516. Valor actual de la función de coste: 1.005
Paso 519. Valor actual de la función de coste: 1.008
Paso 522. Valor actual de la función de coste: 1.005
Paso 525. Valor actual de la función de coste: 1.002
Paso 528. Valor actual de la función de coste: 1.002
Paso 531. Valor actual de la función de coste: 1.003
Paso 534. Valor actual de la función de coste: 1.005
Paso 537. Valor actual de la función de coste: 1.002
Paso 540. Valor actual de la función de coste: 1.002
Paso 543. Valor actual de la función de coste: 1.001
Paso 546. Valor actual de la función de coste: 1.002
Paso 549. Valor actual de la función de coste: 1.002
Paso 552. Valor actual de la función de coste: 1.003
Paso 555. Valor actual de la función de coste: 1.004
Paso 558. Valor actual de la función de coste: 1.013
Paso 561. Valor actual de la función de coste: 1.012
Paso 564. Valor actual de la función de coste: 1.013
Paso 567. Valor actual de la función de coste: 1.015
Paso 570. Valor actual de la función de coste: 1.012
Paso 573. Valor actual de la función de coste: 1.016
Paso 576. Valor actual de la función de coste: 1.021
Paso 579. Valor actual de la función de coste: 1.013
Paso 582. Valor actual de la función de coste: 1.015
Paso 585. Valor actual de la función de coste: 1.012
Paso 588. Valor actual de la función de coste: 1.004
Paso 591. Valor actual de la función de coste: 1.006
Paso 594. Valor actual de la función de coste: 1.008
Paso 597. Valor actual de la función de coste: 1.008
Paso 600. Valor actual de la función de coste: 1.010
Paso 603. Valor actual de la función de coste: 1.011
Paso 606. Valor actual de la función de coste: 1.009
Paso 609. Valor actual de la función de coste: 1.006
Paso 612. Valor actual de la función de coste: 1.008
Paso 615. Valor actual de la función de coste: 1.008
Paso 618. Valor actual de la función de coste: 1.007
Paso 621. Valor actual de la función de coste: 1.010
Paso 624. Valor actual de la función de coste: 1.006
Paso 627. Valor actual de la función de coste: 1.006
Paso 630. Valor actual de la función de coste: 1.006
Paso 633. Valor actual de la función de coste: 1.006
Paso 636. Valor actual de la función de coste: 1.008
Paso 639. Valor actual de la función de coste: 1.003
Paso 642. Valor actual de la función de coste: 1.004
Paso 645. Valor actual de la función de coste: 1.003
Paso 648. Valor actual de la función de coste: 1.002
Paso 651. Valor actual de la función de coste: 1.001
Paso 654. Valor actual de la función de coste: 1.001
Paso 657. Valor actual de la función de coste: 1.001
Paso 660. Valor actual de la función de coste: 1.002
Paso 663. Valor actual de la función de coste: 1.001
Paso 666. Valor actual de la función de coste: 1.002
Paso 669. Valor actual de la función de coste: 1.002
Paso 672. Valor actual de la función de coste: 1.003
Paso 675. Valor actual de la función de coste: 1.002
Paso 678. Valor actual de la función de coste: 1.002
Paso 681. Valor actual de la función de coste: 1.002
Paso 684. Valor actual de la función de coste: 1.003
Paso 687. Valor actual de la función de coste: 1.003
Paso 690. Valor actual de la función de coste: 1.002
Paso 693. Valor actual de la función de coste: 1.003
Paso 696. Valor actual de la función de coste: 1.002
Paso 699. Valor actual de la función de coste: 1.004
Paso 702. Valor actual de la función de coste: 1.005
Paso 705. Valor actual de la función de coste: 1.004
Paso 708. Valor actual de la función de coste: 1.004
Paso 711. Valor actual de la función de coste: 1.004
Paso 714. Valor actual de la función de coste: 1.004
Paso 717. Valor actual de la función de coste: 1.005
Paso 720. Valor actual de la función de coste: 1.006
Paso 723. Valor actual de la función de coste: 1.006
Paso 726. Valor actual de la función de coste: 1.007
Paso 729. Valor actual de la función de coste: 1.006
Paso 732. Valor actual de la función de coste: 1.005
Paso 735. Valor actual de la función de coste: 1.005
Paso 738. Valor actual de la función de coste: 1.008
Paso 741. Valor actual de la función de coste: 1.009
Paso 744. Valor actual de la función de coste: 1.008
Paso 747. Valor actual de la función de coste: 1.009
Paso 750. Valor actual de la función de coste: 1.008
Paso 753. Valor actual de la función de coste: 1.007
Paso 756. Valor actual de la función de coste: 1.007
Paso 759. Valor actual de la función de coste: 1.005
Paso 762. Valor actual de la función de coste: 1.008
Paso 765. Valor actual de la función de coste: 1.005
Paso 768. Valor actual de la función de coste: 1.006
Paso 771. Valor actual de la función de coste: 1.007
Paso 774. Valor actual de la función de coste: 1.008
Paso 777. Valor actual de la función de coste: 1.005
Paso 780. Valor actual de la función de coste: 1.005
Paso 783. Valor actual de la función de coste: 1.004
Paso 786. Valor actual de la función de coste: 1.006
Paso 789. Valor actual de la función de coste: 1.003
Paso 792. Valor actual de la función de coste: 1.002
Paso 795. Valor actual de la función de coste: 1.004
Paso 798. Valor actual de la función de coste: 1.002
Paso 801. Valor actual de la función de coste: 1.003
Paso 804. Valor actual de la función de coste: 1.003
Paso 807. Valor actual de la función de coste: 1.004
Paso 810. Valor actual de la función de coste: 1.005
Paso 813. Valor actual de la función de coste: 1.004
Paso 816. Valor actual de la función de coste: 1.005
Paso 819. Valor actual de la función de coste: 1.002
Paso 822. Valor actual de la función de coste: 1.004
Paso 825. Valor actual de la función de coste: 1.006
Paso 828. Valor actual de la función de coste: 1.003
Paso 831. Valor actual de la función de coste: 1.005
Paso 834. Valor actual de la función de coste: 1.003
Paso 837. Valor actual de la función de coste: 1.002
Paso 840. Valor actual de la función de coste: 1.001
Paso 843. Valor actual de la función de coste: 1.001
Paso 846. Valor actual de la función de coste: 1.002
Paso 849. Valor actual de la función de coste: 1.002
Paso 852. Valor actual de la función de coste: 1.002
Paso 855. Valor actual de la función de coste: 1.002
Paso 858. Valor actual de la función de coste: 1.002
Paso 861. Valor actual de la función de coste: 1.002
Paso 864. Valor actual de la función de coste: 1.003
Paso 867. Valor actual de la función de coste: 1.002
Paso 870. Valor actual de la función de coste: 1.002
Paso 873. Valor actual de la función de coste: 1.001
Paso 876. Valor actual de la función de coste: 1.001
Paso 879. Valor actual de la función de coste: 1.001
Paso 882. Valor actual de la función de coste: 1.002
Paso 885. Valor actual de la función de coste: 1.001
Paso 888. Valor actual de la función de coste: 1.002
Paso 891. Valor actual de la función de coste: 1.002
Paso 894. Valor actual de la función de coste: 1.002
Paso 897. Valor actual de la función de coste: 1.004
Paso 900. Valor actual de la función de coste: 1.005
Paso 903. Valor actual de la función de coste: 1.004
Paso 906. Valor actual de la función de coste: 1.003
Paso 909. Valor actual de la función de coste: 1.003
Paso 912. Valor actual de la función de coste: 1.002
Paso 915. Valor actual de la función de coste: 1.002
Paso 918. Valor actual de la función de coste: 1.001
Paso 921. Valor actual de la función de coste: 1.000
Paso 924. Valor actual de la función de coste: 1.001
Paso 927. Valor actual de la función de coste: 1.001
Paso 930. Valor actual de la función de coste: 1.001
Paso 933. Valor actual de la función de coste: 1.001
Paso 936. Valor actual de la función de coste: 1.002
Paso 939. Valor actual de la función de coste: 1.001
Paso 942. Valor actual de la función de coste: 1.001
Paso 945. Valor actual de la función de coste: 1.000
Paso 948. Valor actual de la función de coste: 1.001
Paso 951. Valor actual de la función de coste: 1.000
Paso 954. Valor actual de la función de coste: 1.000
Paso 957. Valor actual de la función de coste: 1.001
Paso 960. Valor actual de la función de coste: 1.001
Paso 963. Valor actual de la función de coste: 1.000
Paso 966. Valor actual de la función de coste: 1.001
Paso 969. Valor actual de la función de coste: 1.000
Paso 972. Valor actual de la función de coste: 1.002
Paso 975. Valor actual de la función de coste: 1.005
Paso 978. Valor actual de la función de coste: 1.004
Paso 981. Valor actual de la función de coste: 1.003
Paso 984. Valor actual de la función de coste: 1.001
Paso 987. Valor actual de la función de coste: 1.002
Paso 990. Valor actual de la función de coste: 1.001
Paso 993. Valor actual de la función de coste: 1.002
Paso 996. Valor actual de la función de coste: 1.001
Paso 999. Valor actual de la función de coste: 1.002
Los parámetros óptimos para este circuito son: [
0.121, 1.228, 0.041,
0.581, 1.534, 1.718,
-0.181, 1.888, 1.103,
1.106, 1.048, 1.237,
0.05, -0.004, 0.573,
0.275, ]
El valor del autovalor mínimo es: 1.002
# Con la información de las iteraciones podemos dibujar la convergencia de nuestro código
fontsize = 15
plt.rcParams['figure.figsize'] = (15, 7)
plt.plot(range(len(result_energy)), result_energy, label="Valor de la energía", color='red')
plt.xticks(fontsize = fontsize)
plt.yticks(fontsize = fontsize)
plt.xlabel('Paso', fontsize = fontsize)
plt.ylabel('Energía', fontsize = fontsize)
plt.title('Convergencia de la energía con el optimizador SPSA', fontsize = fontsize)
plt.legend(loc='upper right', fontsize = fontsize)
plt.show()
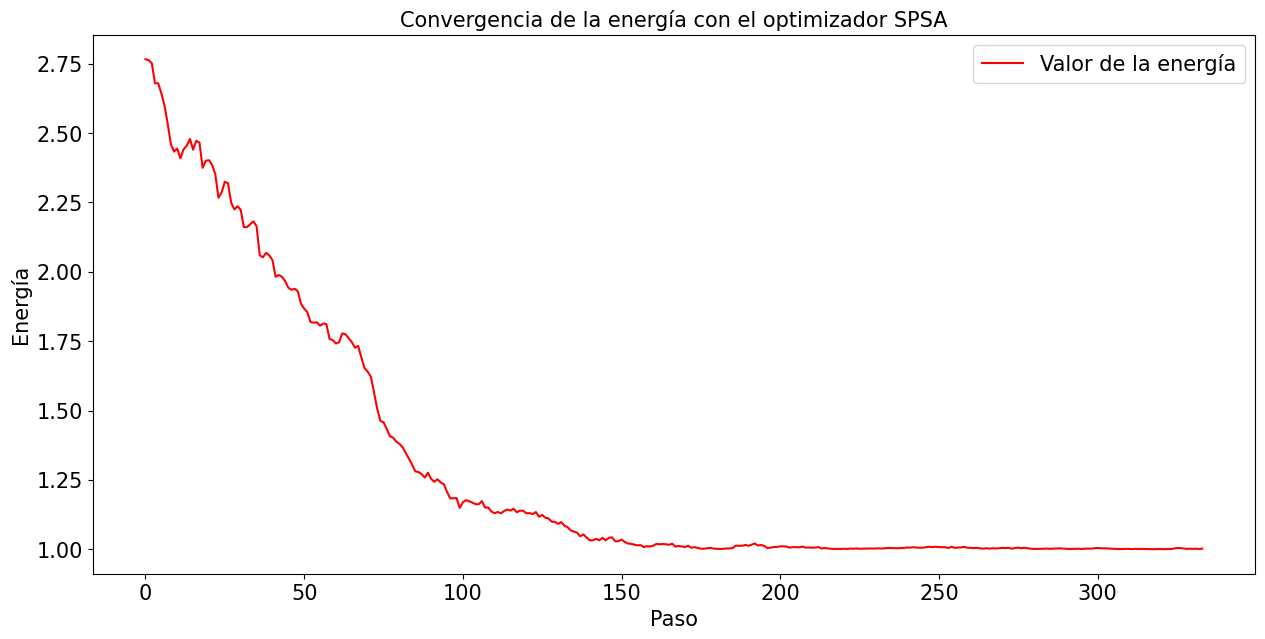
Por supuesto, aunque con este código abordamos los principios básicos del algoritmo y podemos obtener una aproximacion decente de \(E_G\) para matrices pequeñas, este algoritmo se puede implementar de forma más eficaz, rápida y con mayor precisión en operadores de mayor dimensionalidad.
En resumen, en el algoritmo VQE se fabrica un circuito cuántico (ansatz) parametrizado (\(\boldsymbol{\theta}\)), se ejecuta para obtener el valor esperado del operador problema (\(E (\boldsymbol{\theta})\)) y se envía el resultado a un optimizador clásico (SPSA) para que reajuste los parámetros. A lo largo de varias iteraciones, el algoritmo converge a un valor en torno a \(E_G\).
El punto clave del algoritmo VQE, y de los algoritmos variacionales en general, es que, al ser repeticiones de un proceso parametrizado, los posibles errores inducidos por el circuito cuántico (puertas, cross-talking, recaída al fundamental…) al final son contemplados por las sucesivas elecciones de los parámetros, haciéndolo más robusto. Esto hace que, en esta era de la computación NISQ en la que vivimos, sea un algoritmo aplicable e implementable, al menos para casos lo suficientemente sencillos y que no demanden muchos recursos.
Y es una suerte que esto sea así, porque los problemas de diagonalización y obtención del autovalor más bajo son de vital importancia en muchas ramas de la ciencia, como puede ser la química teórica [17], [22] o la física nuclear [6], [9], [20], así como en problemas de otras disciplinas, como la economía (travelling salesman, max-cut) [26].
Los puntos claves de este algoritmo para aumentar las posibilidades y la velocidad de convergencia son la elección del ansatz (que al final determina la cantidad de recursos demandados y varias de las condiciones del problema a resolver) y del algoritmo de optimizador clásico (que debe lidiar con múltiples problemas en el espacio de parámetros, como los mínimos locales o los barren plateaus). En los siguientes apartados de esta documentación hablaremos más sobre estos dos temas.
Authors:
Irais Bautista (CESGA), Sergio Martínez (BIFi-UNIZAR), Jaime Scharfhausen (UAM) y Alejandro Jaramillo (CSUC)






License: Licencia Creative Commons Atribución-CompartirIgual 4.0 Internacional.
This work has been financially supported by the Ministry for Digital Transformation and of Civil Service of the Spanish Government through the QUANTUM ENIA project call - Quantum Spain project, and by the European Union through the Recovery, Transformation and Resilience Plan - NextGenerationEU within the framework of the Digital Spain 2026 Agenda.

