May 06, 2024 | 4 min read
El Modelo de Ising con el algoritmo VQE#
Show code cell source
# Librerías generales
import numpy as np
from collections import defaultdict
from functools import reduce
from itertools import product
import random
import scipy
import matplotlib.pyplot as plt
# Librerías Qibo
import qibo
from qibo import models, gates, hamiltonians
from qibo import matrices as m
# Librerías Qiskit
import qiskit
from qiskit import IBMQ, QuantumCircuit, QuantumRegister, ClassicalRegister, Aer, execute, transpile
from qiskit.visualization import plot_bloch_multivector
from qiskit.algorithms.optimizers import COBYLA, SPSA, POWELL
from qiskit.primitives import Estimator
from qiskit.algorithms.minimum_eigensolvers import VQE
from qiskit.utils import QuantumInstance, algorithm_globals
from qiskit.opflow import X, Z, I, Y
from qiskit.circuit.library import TwoLocal
from qiskit.tools.parallel import parallel_map
random.seed()
qibo.set_backend("numpy")
%matplotlib inline
Introducción al Modelo de Ising#
El Modelo de Ising es un modelo para entender los materiales magnéticos en términos de los spines de los átomos y los electrones que lo forman. Pdemos imaginar el sólido magnético como una red cristalina, y en cada uno de los nodos tenemos una flecha que apunta hacia arriba (\(\uparrow\)) o hacia abajo (\(\downarrow\)). Si dos flechas contiguas apuntan en la misma dirección (\(\uparrow \uparrow\) o \(\downarrow \downarrow\)), esta unión tiene una contribución negativa a la energía del sistema: el sistema tiende a alinear los spines entre si. Por otro lado si las flechas apuntan en direcciones contrarias (\(\uparrow \downarrow\)), la energía de esa unión es positiva: al sistema le “cuesta” mantener flechas en direcciones opuestas.
Existen dos factores externos que pueden condicionar el estado del sistema: el campo magnético y la temperatura a los que lo sometemos. Por un lado, si introducimos un campo magnético apuntando hacia arriba, los spines tienden a alinearse con el campo, por lo que todos querrán apuntar hacia arriba. Por otro lado, si calentamos mucho el sistema, las excitaciones térmicas provocarán que los spines se agiten, cambiando de dirección y desordenándose.
En el caso cuántico, las fluctuaciones cuánticas del sistema provocan cambios en estos spines incluso a temperatura cero, permitiendo la existencia de transiciones de fase cuánticas.
Podemos expresar el Hamiltoniano del sistema como:
donde \(J\) es la contribución energética de la interacción de dos spines adyacentes (fijémonos en que en el primer sumatorio solo se suma a primeros vecinos, \(\langle i,j \rangle\)) y \(h\) está relacionado con este campo magnético externo. \(\sigma_i\) es la “etiqueta” del spin y vale \(+1\) o \(-1\) según apunte hacia arriba o hacia abajo.
Este problema puede complicarse dados diferentes factores microcópicos como la estructura cristalina o incluso tener interacciones más allá de los primeros vecinos, lo que requiere métodos aproximados para solucionarlo. No obstante, hay dos casos especiales para los que existe una solución exacta y analítica del modelo: cuando el sistema tiene solo una dimensión o cuando el sistema tiene dos dimensiones y una estructura cuadrada.
El Modelo de Ising 1D#
Vamos a analizar el caso cuántico de la cadena de Ising unidimensional. Precisamente por la naturaleza cuántica del problema podemos utilizar las matrices de Pauli para caracterizar el Hamiltoniano, dando lugar a una nueva forma del operador [1]:
siendo \(N\) la longitud de la cadena y, de nuevo, \(J\) está relacionado con la energía del sistema y \(g\) con la intensidad del campo magnético a primeros vecinos. \(X_i\) y \(Z_i\) son operadores de Pauli como los que introducíamos al principio de este documento, actuando sobre el spin en posición \(i\).
Este modelo se conoce como transverse field Ising Model. A veces se define \(\Gamma = J g\), donde \(\Gamma\) se conoce como campo transverso.
Nota (Notación reducida)
En lo que a la descomposición de Pauli se refiere, los productos anteriores realmente son productos tensoriales de operadores para las partículas \(i\) e \(i+1\), teniendo identidades en el resto de posiciones. Por ejemplo, para una cadena de tres spines, \(N=3\),
donde hemos tomado condiciones de contorno periódicas (\(\sigma_{N+1} \rightarrow \sigma_1\)).
Show code cell source
PAULIS = {
"I": np.eye(2, dtype=complex),
"X": np.array([[0,1],[1,0]], dtype=complex),
"Y": np.array([[0,-1j],[1j,0]], dtype=complex),
"Z": np.array([[1,0],[0,-1]], dtype=complex)
}
Vamos a redefinir nuestras constantes del problema \(J\) y \(g\) de forma que podamos expresarlas como magnitudes relativas, escribiendo nuestro operador como
Ahora los signos (\(-\)) han pasado a ser positivos y solo tenemos una constante de acoplo, \(\gamma\). Esto implica que, cuando \(\gamma\) es positivo estamos en el caso ferromagnético y cuando es negativo en el antiferromagnético.
La función que implementa esto es la siguiente:
def ising_chain_ham_qibo(n, gam):
# Esta función nos devuelve el Hamiltoniano en términos utilizables por los algoritmos de Qibo
# n = number of spin positions
# gam = transverse field parameter
from qibo.symbols import X, Z
sym_X = sum(X(i) * X(i+1) for i in range(n-1)) + (X(0) * X(n-1))
sym_Z = sum(Z(i) for i in range(n))
sym_H = sym_X + gam * sym_Z
H = hamiltonians.SymbolicHamiltonian(sym_H)
return H, H.matrix
def ising_chain_ham(n, gam):
# Esta función nos devuelve el Hamiltoniano en términos utilizables por los algoritmos de Qiskit
# n = number of spin positions
# gam = transverse field parameter
for i in range(n):
vecX = [I] * n
vecZ = [I] * n
vecX[i] = X
vecZ[i] = Z
if i == n - 1:
vecX[0] = X
else:
vecX[i+1] = X
auxX = vecX[0]
auxZ = vecZ[0]
for a in vecX[1:n]:
auxX = auxX ^ a
for b in vecZ[1:n]:
auxZ = auxZ ^ b
if i == 0:
H = (auxX) + (gam * auxZ)
else:
H = H + (auxX) + (gam * auxZ)
return H
def ising_chain_matrix(n, gam):
# Esta función devuelve el Hamiltoniano como un array (lista de listas)
for i in range(n):
HX = [PAULIS["I"]] * n
HZ = [PAULIS["I"]] * n
HX[i] = PAULIS["X"]
HZ[i] = PAULIS["Z"]
if i == n - 1:
HX[0] = PAULIS["X"]
else:
HX[i+1] = PAULIS["X"]
aux = reduce(np.kron, HZ)
aux = [val * gam for val in aux]
if i == 0:
H = reduce(np.kron, HX) + aux
else:
H = H + reduce(np.kron, HX) + aux
return H
Vamos a resolver una cadena de Ising de \(N = 4\) spines. Entonces prepararemos el Hamiltoniano y después le haremos una serie de transformaciones que nos permiten diagonalizarlo.
Empezamos por escribir nuestro operador. Como tenemos \(N=4\) spines, el operador será
Tomemos un valor de \(\gamma\) pequeño, por ejemplo, \(\gamma = 0.3\).
# Definimos el Hamiltoniano
n = 4
gam = .3
op_H, matrix = ising_chain_ham_qibo(n,gam)
# Definimos el Hamiltoniano
n = 4
gam = 0.3
op_H = ising_chain_ham(n,gam)
matrix = ising_chain_matrix(n, gam)
[Qibo 0.1.12.dev0|WARNING|2024-05-22 13:14:38]: Calculating the dense form of a symbolic Hamiltonian. This operation is memory inefficient.
# Ahora creamos un circuito variacional de ansatz
# En este caso usamos un circuito de puertas RY(theta) y CZ, haciendo los diferentes valores de theta aleatorios
nqubits = n
nlayers = 8
circuit = models.Circuit(nqubits)
for l in range(nlayers):
circuit.add((gates.RY(q, theta=0) for q in range(nqubits)))
circuit.add((gates.CZ(q, q+1) for q in range(0, nqubits-1, 2)))
circuit.add((gates.RY(q, theta=0) for q in range(nqubits)))
circuit.add((gates.CZ(q, q+1) for q in range(1, nqubits-2, 2)))
circuit.add(gates.CZ(0, nqubits-1))
circuit.add((gates.RY(q, theta=0) for q in range(nqubits)))
# Ahora creamos un circuito variacional de ansatz
# En este caso usamos un circuito de puertas RY(theta) y CZ, haciendo los diferentes valores de theta aleatorios
ansatz_circ = TwoLocal(num_qubits=n, rotation_blocks='ry', entanglement_blocks='cz')
En este caso, en lugar de utilizar el optimizador SPSA como hicimos en la sección anterior, empleamos uno nuevo: el método de Powell [2].
Nota (Eficiencia en la optimización)
El algoritmo de Powell que estamos empleando es considerablemente más eficiente que el resto de algoritmos que hemos probado para este problema específicamente. No obstante, su funcionamiento da lugar a unas gráficas de convergencia que no son particularmente ilustrativas. Si se quiere ver una gráfica en la que realmente se aprecie la convergencia del algoritmo, se puede probar a utilizar el algoritmo COBYLA. No obstante, la ejecución del código tardará un tiempo considerable (del orden de 20 minutos).
# Especificamos el algorimto de optimización clásica
# opt = 'COBYLA'
opt = 'Powell'
# Especificamos el algorimto de optimización clásica
# opt = COBYLA(maxiter = 10000)
opt = POWELL()
Implementamos unas funciones de callback para poder almacenar los datos de cada iteración y hacer un análisis de la convergencia.
# Esto son funciones auxiliares para guardar los datos de las iteraciones
intermediate_info = {
'parameters': [],
'energy': [],
#'stddev': []
}
def callback(p):
intermediate_info['parameters'].append(p)
energy, _, _ = vqe.minimize(p, callback = None, method=opt, options = None, compile=False)
intermediate_info['energy'].append(energy)
#intermediate_info['stddev'].append(stddev)
# Esto son funciones auxiliares para guardar los datos de las iteraciones
counts = []
values = []
def store_intermediate_result(eval_count, parameters, mean, std):
counts.append(eval_count)
values.append(mean)
Como anticipamos previamente, vamos a hacer uso de la función vqe que está ya implementada, ya que es considerablemente más eficiente que la que programamos en la sección anterior.
# Parámetros del Ansatz
initial_parameters = np.random.uniform(-2*np.pi, 2*np.pi, 2*nqubits*nlayers + nqubits)
# Construcción del método VQE
vqe = models.VQE(circuit, op_H)
options = {'disp': True, 'return_all': True}
# Y ejecutamos el algoritmo
best, params, extra = vqe.minimize(initial_parameters, callback = callback, method=opt, options = options, compile=False)
values = intermediate_info['energy']
# Simulador/Ordenador cuántico
backend = Aer.get_backend('statevector_simulator')
# Entorno para la resolución
algorithm_globals.random_seed = 63
qi = QuantumInstance(backend, seed_transpiler=63, seed_simulator=63)
# Algoritmo VQE, introduciendo el ansatz y el optimizador elegidos
vqe_proc = VQE(estimator = Estimator() ,ansatz=ansatz_circ, optimizer=opt, callback=store_intermediate_result)
vqe_proc.quantum_instance = qi
# Resultados
sol = vqe_proc.compute_minimum_eigenvalue(operator = op_H)
# print(sol, "\n")
best = sol.optimal_value
Optimization terminated successfully.
Current function value: -4.089306
Iterations: 3
Function evaluations: 1871
# Y ya vemos el valor de la solución:
print("E_G =",best)
E_G = -4.089305581262189
# Con la información de las iteraciones podemos dibujar la convergencia de nuestro código
fontsize = 15
plt.rcParams['figure.figsize'] = (15, 7)
plt.plot(range(len(values)), values, label="Energy value", color='red')
plt.xticks(fontsize = fontsize)
plt.yticks(fontsize = fontsize)
plt.xlabel('Steps', fontsize = fontsize)
plt.ylabel('Energy', fontsize = fontsize)
plt.title('Energy convergence for Powell optimizer', fontsize = fontsize)
plt.legend(loc='upper right', fontsize = fontsize);
plt.show()
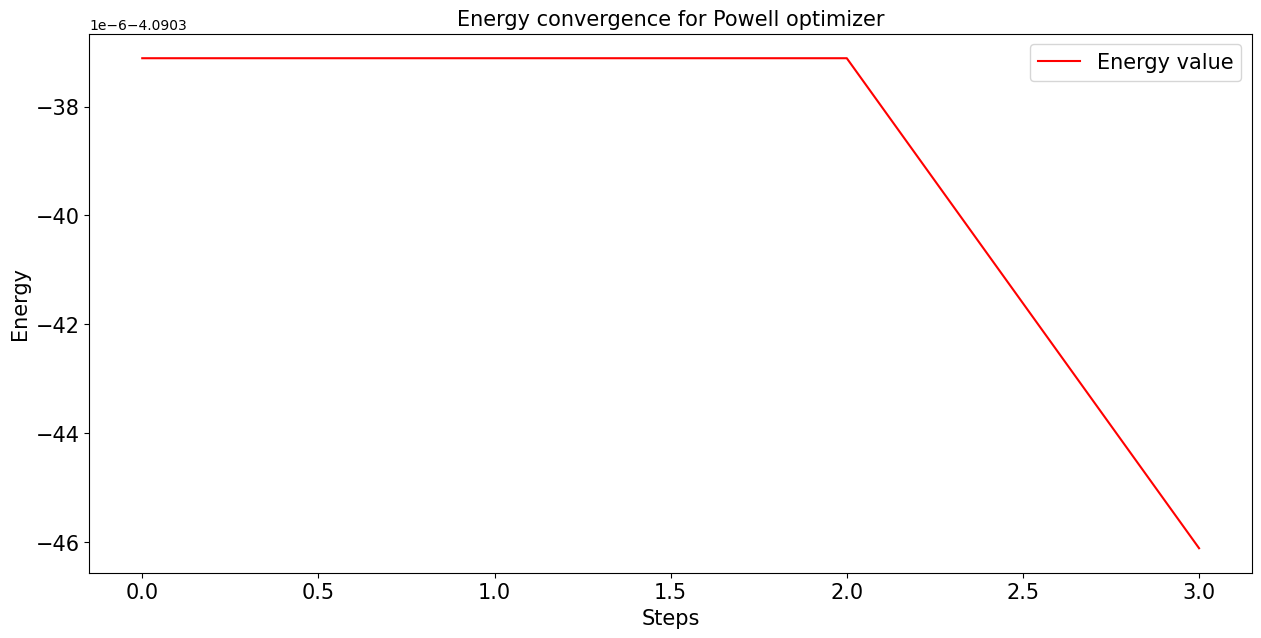
También comparamos con el valor que obtenemos simplemente de diagonalizar la matriz, ya que, al ser “pequeña” (\(16 \times 16\)), scipy no tiene problema en hacerlo.
eigvals, eigvecs = scipy.linalg.eig(matrix)
print("E_G =", min(eigvals).real)
print("Error relativo =", abs((best - min(eigvals).real)/min(eigvals).real) * 100, "%")
E_G = -4.092961599426855
Error relativo = 0.08932451663308086 %
Bibliografía#
- 1
Alba Cervera-Lierta. Exact Ising model simulation on a quantum computer. Quantum, 2:114, December 2018. Publisher: Verein zur Förderung des Open Access Publizierens in den Quantenwissenschaften. URL: https://quantum-journal.org/papers/q-2018-12-21-114/ (visited on 2022-12-19), doi:10.22331/q-2018-12-21-114.
- 2
M. J. D. Powell. An efficient method for finding the minimum of a function of several variables without calculating derivatives. The Computer Journal, 7(2):155–162, January 1964. URL: https://doi.org/10.1093/comjnl/7.2.155 (visited on 2023-06-23), doi:10.1093/comjnl/7.2.155.
Authors:
Irais Bautista (CESGA), Sergio Martínez (BIFi-UNIZAR), Jaime Scharfhausen (UAM) y Alejandro Jaramillo (CSUC)
License: Licencia Creative Commons Atribución-CompartirIgual 4.0 Internacional.
This work has been financially supported by the Ministry for Digital Transformation and of Civil Service of the Spanish Government through the QUANTUM ENIA project call - Quantum Spain project, and by the European Union through the Recovery, Transformation and Resilience Plan - NextGenerationEU within the framework of the Digital Spain 2026 Agenda.
