Jun 03, 2025 | 1 min read
\( \newcommand{\bra}[1]{\langle #1|} \) \( \newcommand{\ket}[1]{|#1\rangle} \) \( \newcommand{\branew}[1]{\langle #1|} \) \( \newcommand{\ketnew}[1]{\langle #1|} \) \( \newcommand{\braket}[2]{\langle #1|#2\rangle} \) \( \newcommand{\ketbra}[2]{| #1\rangle \langle #2 |} \) \( \newcommand{\i}{{\color{blue} i}} \) \( \newcommand{\Hil}{{\cal H}} \) \( \newcommand{\cg}[1]{{\rm C}#1} \) \( \newcommand{\lp}{\left(} \) \( \newcommand{\rp}{\right)} \) \( \newcommand{\lc}{\left[} \) \( \newcommand{\rc}{\right]} \) \( \newcommand{\lch}{\left\{} \) \( \newcommand{\rch}{\right\}} \) \( \newcommand{\Lp}{\Bigl(} \) \( \newcommand{\Rp}{\Bigr)} \) \( \newcommand{\Lc}{\Bigl[} \) \( \newcommand{\Rc}{\Bigr]} \) \( \newcommand{\Lch}{\Bigl\{} \) \( \newcommand{\Rch}{\Bigr\}} \) \( \newcommand{\rqa}{\quad \Rightarrow \quad} \) \( \newcommand{\bm}{\boldsymbol}\)
1.4. Pulso de microondas#
A lo largo de los siguientes capítulos se va usar bastante el concepto de pulso de frecuencia \(\omega\) (en concreto, en el rango de las microondas). Lo importante para entender estos capítulos es tener en cuenta que cuando hablamos de un pulso hablamos de un pulso electromagnético, es decir, de una onda electromagnética de una cierta frecuencia \(\omega\). Las ondas electromagnéticas están compuestas de fotones (al igual que la luz, pues esta no es más que una onda electromagnética en un rango de frecuencias que podemos ver con nuestros ojos).
El concepto clave aquí es que estos fotones son cuantos de energía (paquetitos de energía), y estos cuantos tiene una energía muy concreta que depende de la frecuencia de la onda electromagnética:
donde \(\hbar\) es la constante de Plack y \(\omega\) es la frecuencia de la onda.
Es decir, un pulso (onda electromagnética) de frecuencia \(\omega\) va estar compuesta de fotones con energía \(\hbar \omega\). Si cambiamos la frecuencia del pulso, cambiamos la energía de los fotoness que lo componen.
A lo largo los capítulos se usará el hecho de que si tenemos un sistema cuántico con varios niveles de energía, podemos hacer que el sistema pase de estar en un nivel de energía a estar en el siguiente, si le mandamos fotones con la energía exacta de la transición, es decir, con un pulso con una frecuencia muy concreta.
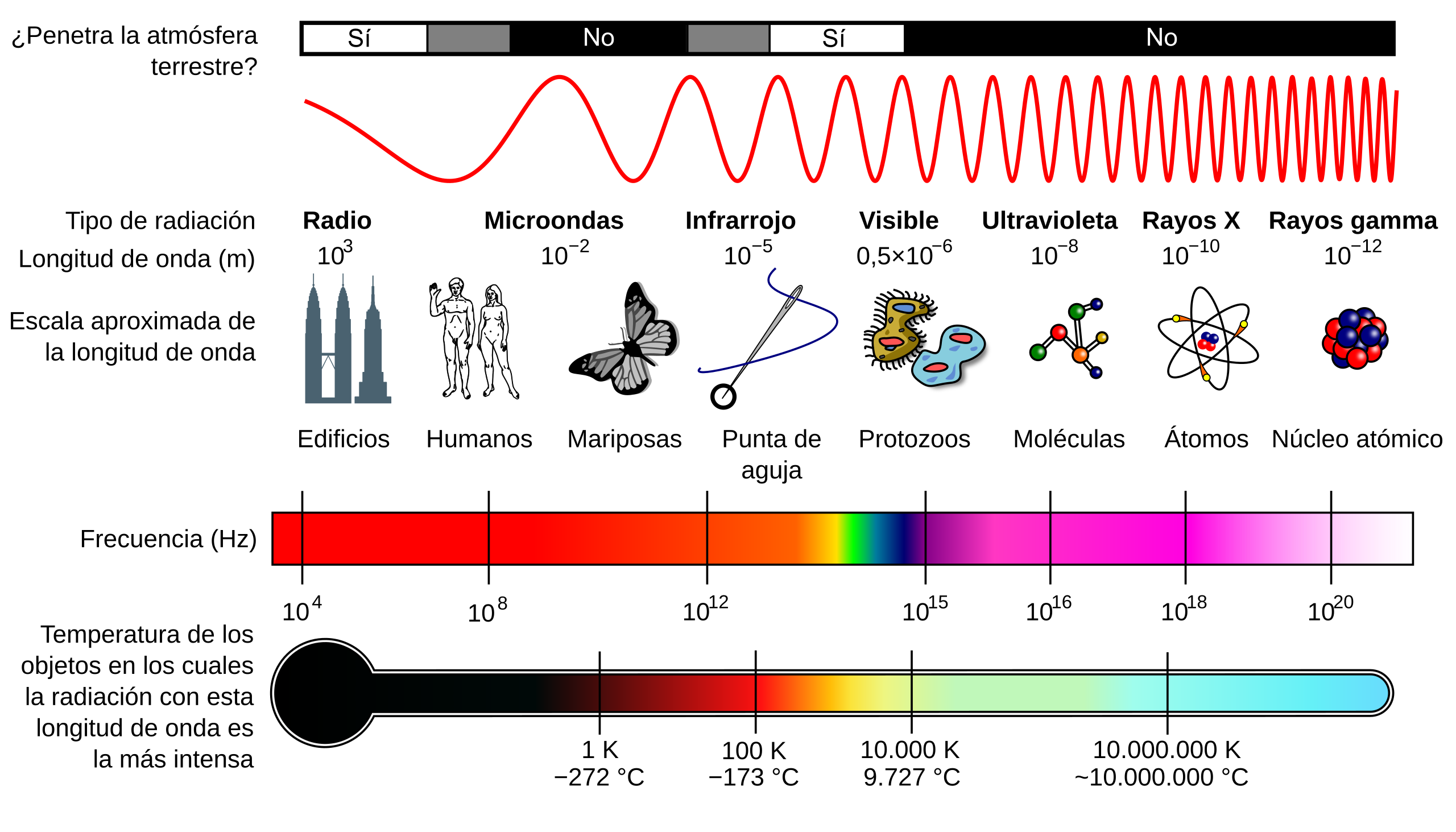
Fig. 1.4 Espectro electromagnético#
Autor:
David Castaño (UMA-SCBI)



License: Licencia Creative Commons Atribución-CompartirIgual 4.0 Internacional.
This work has been financially supported by the Ministry for Digital Transformation and of Civil Service of the Spanish Government through the QUANTUM ENIA project call - Quantum Spain project, and by the European Union through the Recovery, Transformation and Resilience Plan - NextGenerationEU within the framework of the Digital Spain 2026 Agenda.

