qubits de RMN

\( \newcommand{\bra}[1]{\langle #1|} \) \( \newcommand{\ket}[1]{|#1\rangle} \) \( \newcommand{\branew}[1]{\langle #1|} \) \( \newcommand{\ketnew}[1]{\langle #1|} \) \( \newcommand{\braket}[2]{\langle #1|#2\rangle} \) \( \newcommand{\ketbra}[2]{| #1\rangle \langle #2 |} \) \( \newcommand{\i}{{\color{blue} i}} \) \( \newcommand{\Hil}{{\cal H}} \) \( \newcommand{\cg}[1]{{\rm C}#1} \) \( \newcommand{\lp}{\left(} \) \( \newcommand{\rp}{\right)} \) \( \newcommand{\lc}{\left[} \) \( \newcommand{\rc}{\right]} \) \( \newcommand{\lch}{\left\{} \) \( \newcommand{\rch}{\right\}} \) \( \newcommand{\Lp}{\Bigl(} \) \( \newcommand{\Rp}{\Bigr)} \) \( \newcommand{\Lc}{\Bigl[} \) \( \newcommand{\Rc}{\Bigr]} \) \( \newcommand{\Lch}{\Bigl\{} \) \( \newcommand{\Rch}{\Bigr\}} \) \( \newcommand{\rqa}{\quad \Rightarrow \quad} \) \( \newcommand{\bm}{\boldsymbol}\)

4.3. qubits de RMN#

En esta sección vamos a describir como es el sistema con el que se construyen los qubits en RNM, basándonos en su Hamiltoniano del sistema y su Hamiltoniano de control. El Hamiltoniano del sistema da la energía de los espines simples y acoplados en un campo magnético estático, y el Hamiltoniano de control surge de la aplicación de pulsos de radiofrecuencia al sistema en, o cerca de, sus frecuencias resonantes. Veremos que para describir el efecto de los pulsos es más conveniente usar un sistema de referencia giratorio.

4.3.1. Hamiltoniano del sistema#

4.3.1.1. Espines simples.#

Una partícula con espín constituye un dipolo magnético. En esencia, dipolo magnético es un pequeño imán, es decir, una fuente de campo magnético. El momento dipolar magnético, \(\vec{\mu}\), es proporcional al momento angular de espín, \(\vec{S}\):

(4.9)#\[\begin{equation} \vec{\mu} = \gamma \vec{S}\, , \end{equation} \]

donde la constate de proporcionalidad, \(\gamma\), se denomina ratio giromagnético (gyromagnetic ratio). Este toma la forma

(4.10)#\[\begin{equation} \gamma = g \frac{q}{2m} \, , \end{equation} \]

donde \(q\) es la carga eléctrica de la partícula, \(m\) su masa y \(g\) se denomina factor \(g\) (\(g\)-factor).

Cuando un dipolo magnético se sitúa en un campo magnético \(\vec{B}\), este dipolo experimenta un torque, \(\vec{\mu} \times \vec{B}\), que tiende a alinearlo paralelo al campo (como la aguja de una brújula). La energía asociada con este torque es

(4.11)#\[\begin{equation} E = - \vec{\mu} \cdot \vec{B} \end{equation}\]

con lo que el Hamiltoniano para una partícula cargada con espín, en reposo en un campo magnético \(\vec{B}\), es

(4.12)#\[\begin{equation} \mathcal{H} = - \gamma \vec{B} \cdot \vec{S} \end{equation}\]

donde \(S\) es el operador de espín (ver Ec. (4.5) para el caso de partículad de espín 1/2).

Si tenemos una partícula (o un núcleo) de espín 1/2 (no consideraremos espines de mayor orden en estas notas) en un campo magnético \(\vec{B}\) a lo largo del eje \(\hat{z}\), entonces su evolución temporal está gobernada por el Hamiltoniano

(4.13)#\[\begin{split}\begin{equation} \boxed{\mathcal{H} = - \gamma B_0 S_z = - \omega_0 S_z = \begin{bmatrix} - \hbar \omega_0/2 & 0 \\ 0 & \hbar \omega_0 /2 \end{bmatrix}} \, , \end{equation} \end{split}\]

donde

\(\gamma\) es ratio giromagnético del núcleo (ver Ec. (4.10)),
\(\omega/2 \pi = \gamma B_0 \) es la frecuencia de Larmor
e \(S_z\) es el operador de espín en la dirección \(\hat{z}\) (ver Ec. (4.7)).

Nota (frecuencia y frecuencia angular)

En Física, la frecuencia se define como el inverso del periodo de rotación: \(f = 1/T\) y se mide en Hz (1/segundos). Además, se define la frecuencia angular como \(\omega = 2\pi f\) y se mide en radianes/segundo. Muchas veces se denomina a las dos, simplemente, frecuencia.

La interpretación de la Ec. (4.13) es simple. Cuando tenemos una partícula de espín 1/2 aislada, las dos proyecciones del espín son degeneradas, es decir, tiene la misma energía. Esto es fácil de entender si pensamos en que no hay ninguna dirección privilegiada en el sistema. Cuando introducimos un campo magnético, ahora sí hay una dirección privilegiada: aquella con el momento dipolar magnético \(\vec{\mu}\) apuntando en la misma dirección que el campo magnético. Esto es debido a que el espín es como un pequeño imán y tiende a orientarse con el campo magnéticos. En este momento, el sistema pasa a ser no-degenerado, y un estado tiene más energía que el otro.

Esto último se traduce matemáticamente en la Ec. (4.13). Como el Hamiltoniano es diagonal, los elementos de la diagonal son las energías de los estados. Vemos que el estado con el espín apuntando en la misma dirección (es estado \(\ket{0}\) o \(\ket{\uparrow}\)) que el campo magnético tiene menos energía que el estado que apunta en la dirección contraria (el estado \(\ket{1}\) o \(\ket{\downarrow}\)). La diferencia de energía entre los estados es de \(\hbar \omega_0\), como se puede ver en la Fig. 4.1. Esta separación de energías (energy splitting) se conoce como Zeeman spliting.

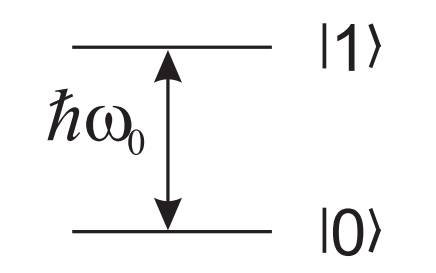
../../../_images/Fig_Harware_NMR_split_Zeeman.png — Fig. 4.1 Diagrama de energías de una partícula de espín 1/2 en un campo magnético.#

Podemos entender gráficamente la evolución temporal \(U = e^{-i \mathcal{H} t/ \hbar}\) bajo el Hamiltoniano de la Ec. (4.13) como un movimiento de precesión en la esfera de Bloch al rededor de \(\vec{B}_0\), como se muestra en la Fig. 4.2. Como es habitual, definimos el eje \(\hat{z}\) de la esfera de Bloch como el eje de cuantización del Hamiltoniano, con \(\ket{0}\) a lo largo de \(+\hat{z}\) y \(\ket{1}\) a lo largo de \(-\hat{z}\).

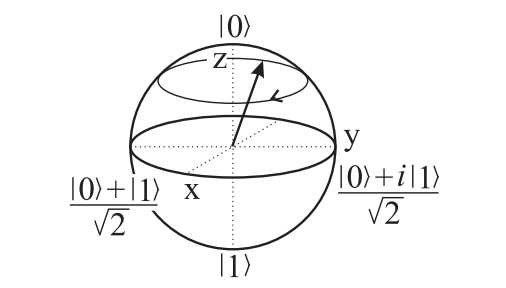
../../../_images/Fig_Harware_NMR_precesion.png — Fig. 4.2 Precesión del valor esperado del espín entorno al campo magnético.#

Nota (Esfera de Bloch para el espín)

Véase que para el espín la representación en la esfera de Bloch no es más que la representación en 3D del vector de espín.

Nota (orientación del espín)

En las Ecs. (4.9) y (4.10) vemos que el vector de espín y el momento dipolar magnético se relacionan por una constate que \(\gamma\) que puede ser positiva o negativa, dependiendo del valor de la carga eléctrica de la partícula. Es decir, estos vectores pueden apuntar en la misma dirección o en dirección opuesta.

Hemos comentado que cuando tenemos un campo magnético, el estado de menor energía es aquel con el momento dipolar magnético apuntando en la dirección del campo. Como podemos ver en la Fig. 4.3, tenemos dos opciones dependiendo de la carga de la partícula.

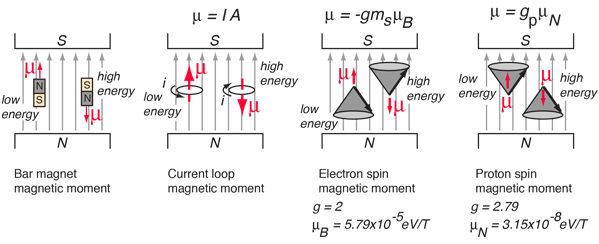
../../../_images/Fig_Hardware_NMR_espines_en_B.png — Fig. 4.3 Momentos dipolares magnéticos en presencia de un campo magnético externo. En las dos figuras de la derecha vemos que, dependiendo de la carga de la partícula, el momento dipolar puede apuntar en la misma dirección o en la contraria al espín. Figura tomada de \url{http://hyperphysics.phy-astr.gsu.edu/hbase/Nuclear/nmr.html}#

Vemos a la demostración de que el valor esperado del espín precesa entorno al campo magnético:

Demostración

(Precesión de Larmor, Griffiths [8] ejemplo 4.3)

Supongamos una partícula con espín 1/2 sometida a un campo magnético en la dirección \(\vec{z}\), i.e. \(\vec{B}_0 = B_0 \hat{z}\). El Hamiltoniano estará dado por

(4.14)#\[\begin{equation} \mathcal{H} = - \gamma B_0 S_z = - \frac{\gamma B_0 \hbar}{2} \begin{bmatrix}1 & 0 \\ 0 & -1 \end{bmatrix} \end{equation}\]

Los autovectores y autovalores (energías) de este Hamiltoniano son

(4.15)#\[\begin{equation} \lch \begin{matrix} \ket{0} = \begin{bmatrix} 1 \\ 0 \end{bmatrix} \, \text{con energía } E_{\ket{0}} = - (\gamma B_0 \hbar) /2 \, \\ \ket{1} = \begin{bmatrix} 0 \\ 1 \end{bmatrix} \, \text{con energía } E_{\ket{1}} = + (\gamma B_0 \hbar) / 2 \end{matrix} \right. \end{equation}\]

La energía es menor cando el momento dipolar es paralelo al campo magnético, al igual que en el caso clásico.

Como el Hamiltoniano es independiente del tiempo, la solución general para la ecuación de Schrödinger dependiente de tiempo,

(4.16)#\[\begin{equation} i \hbar \frac{\partial \ket{\Psi}}{\partial t} = \mathcal{H} \ket{\Psi} \end{equation} \]

puede expresarse en función de estados estacionarios:

(4.17)#\[\begin{split}\begin{equation} \ket{\Psi (t)} = a e^{-i E_{\ket{0}} t/ \hbar} \ket{0} + b e^{-i E_{\ket{1}} t/ \hbar} \ket{1} = \begin{bmatrix} a e ^{i \gamma B_0 t/2} \\ b e ^{i \gamma B_0 t/2} \end{bmatrix} \end{equation} \end{split}\]

Las constantes \(a\) y \(b\) se pueden determinar mediante las condiciones iniciales:

(4.18)#\[\begin{equation} \ket{\Psi (t = 0)} = \begin{bmatrix} a \\ b\end{bmatrix} \end{equation}\]

(por supuesto, \(|a|^2 + |b|^2 = 1\)). Sin perdida de generalidad, podemos elegir \(a = \cos (\alpha/2)\) y \(b = \sin (\alpha/2)\), donde \(\alpha\) es un ángulo fijo cuyo significado físico veremos dentro de poco. Tenemos entonces

(4.19)#\[\begin{equation} \ket{\Psi (t)} = \begin{bmatrix} \cos (\alpha/2) e^{i \gamma B_0 t/2} \\ \sin (\alpha/2) e^{-i \gamma B_0 t/2} \end{bmatrix} \end{equation}\]

Para ver que está pasando con el espín bajo la evolución de este Hamiltoniano, calculemos el calor esperado del espín \(\vec{S}\) como función del tiempo.

(4.20)#\[\begin{equation} \begin{aligned} \left\langle S_x \right\rangle = & \, \bra{\Psi(t)} S_x \ket{\Psi(t)} = \nonumber \\ = & \, \Lc \psi_0^* \quad \psi_1^* \Rc \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \begin{bmatrix} \psi_0 \\ \psi_1 \end{bmatrix} \nonumber \\ = & \, \Lc a e ^{-i \gamma B_0 t/2} \qquad b e ^{-i \gamma B_0 t/2} \Rc \frac{\hbar}{2} \begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix} \begin{bmatrix} \cos (\alpha/2) e^{i \gamma B_0 t/2} \\ \sin (\alpha/2) e^{-i \gamma B_0 t/2} \end{bmatrix} \nonumber \\ = & \, \frac{\hbar}{2} \sin \alpha \cos (\gamma B_0 t ) \end{aligned} \end{equation}\]

De forma análoga,

(4.21)#\[\begin{equation} \begin{aligned} \left\langle S_y \right\rangle = & \, - \frac{\hbar}{2} \sin \alpha \sin (\gamma B_0 t ) \\ \left\langle S_z \right\rangle = & \frac{\hbar}{2} \cos \alpha \end{aligned} \end{equation}\]

Con lo cual, \(\left\langle \vec{S} \right\rangle\) está inclinado un ángulo \(\alpha\) respecto al eje \(\hat{z}\), y precesa al rededor del campo con una frecuencia

(4.22)#\[\begin{equation} f_0 = \omega_0 / 2 \pi = \gamma B_0 / 2 \pi \end{equation}\]

(la frecuencia de Larmor) al igual que en el caso clásico (una peonza inclinada). No tenemos ninguna sorpresa aquí, pues el teorema de Ehrenfest nos asegura que los valores esperados evolucionan de acuerdo a las leyes clásicas del movimiento (algunos autores limitan esta afirmación solo al par de ecuaciones \(\left\langle p \right\rangle = m d \left\langle x \right\rangle / dt\) y \(\left\langle - \partial V / \partial x \right\rangle = d \left\langle p \right\rangle / dt\)) Puede verse esto en el Griffiths, [8].

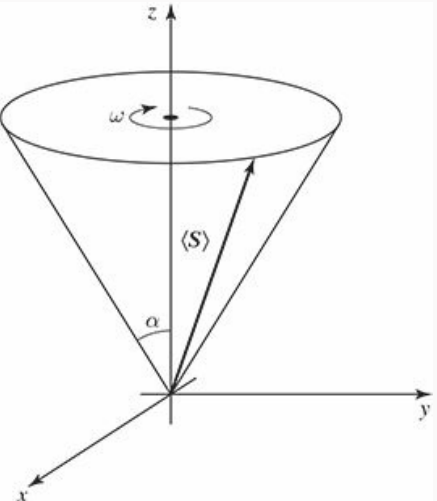
../../../_images/Fig_Harware_NMR_precession_griffiths.png — Fig. 4.4 Precesión de Larmor en un campo magnético uniforme.#

Ejercicio

Verifica que la Ec. (4.17) es solución de la ecuación de Schrödinger, Ec. (4.16)

El Hamiltoniano de espín para una molécula con \(n\) núcleos desacoplados viene dado por

(4.23)#\[\begin{equation} \mathcal{H}_0 = - \sum_{i=1}^n \omega_0^i S_z^i \end{equation} \]

Véase que, los espines de especies nucleares diferentes (espines heteronucleares) tendrán diferentes valores de \(\omega_0^i\), así como también es posibles que los espines de la misma especie nuclear (espines homonucleares) que formen una molécula tengan también diferentes valores de esta frecuencia.

4.3.1.2. Espines que interactúan.#

Para espines nucleares en moléculas, la naturaleza nos proporciona dos mecanismos de interacción diferentes que vamos a describir:

Interacción directa dipolo-dipolo. La interacción magnética dipolo-dipolo es similar a la interacción entre dos barras magnéticas cercanas. Tiene lugar puramente a través del espacio (no se requiere ningún medio para esta interacción) y depende del vector internuclear \(\vec{r}_{ij}\) que conecta los dos núcleos \(i\) y \(j\), tal y como describe el Hamiltoniano

(4.24)#\[\begin{equation} \mathcal{H}_D = \sum_{i<j} \frac{\mu_0 \gamma_i \gamma_j}{4 \pi | \vec{r}_{ij}|^3 \hbar} \lc \vec{S}^i \cdot \vec{S}^j - \frac{3}{| \vec{r}_{ij}|^2} \lp \vec{S}^i \cdot \vec{r}_{ij} \rp \lp \vec{S}^j \cdot \vec{r}_{ij} \rp \rc \end{equation} \]

donde \(\mu_0\) es la permeabilidad magnética habitual del espacio libre. No vamos a entrar en dalles sobre esta interacción, pues usualmente se promedia y no tiene efecto.
Interacción del contrato de Fermi mediada por electrones (acoplamiento J). El segundo mecanismo de interacción entre los espines nucleares de una molécula es el acoplamiento \(J\) o acoplamiento escalar. Esta interacción está mediada por los electrones compartidos en los enlaces químicos entre los átomos, y es debido al solapamiento de la función de onda del electrón compartido con los dos núcleos acoplados. Es decir, una interacción de contacto de Fermi. La fuerza de acoplamiento de enlace J depende de la especie nuclear respectiva y disminuye con el número de enlaces químicos que separan los núcleos. El Hamiltoniano es

(4.25)#\[\begin{equation} \mathcal{H} = \frac{1}{\hbar} \sum_{i <j} 2 \pi J_{ij} S^i S^j = \frac{1}{\hbar} \sum_{i < j} 2 \pi J_{ij} \lp S_x^i S_x^j + S_y^i S_y^j + S_z^i S_z^j \rp \end{equation}\]

donde \(J_{ij}\) es la fuerza de acoplamiento entre los espines \(i\) y \(j\). Cuando \(| \omega_0^i - \omega_0^j |\) es mucho más grande que el acoplamiento \(J_{ij}\) (\(| \omega_0^i - \omega_0^j | \gg 2 \pi |J_{ij}|\)), los acoplamiento transversos se pueden despreciar. De esta forma, el Hamiltoniano se simplifica

(4.26)#\[\begin{equation} \boxed{\mathcal{H}_j = \frac{1}{\hbar} \sum_{i < j}^n 2 \pi J_{ij} S_z^{i} S_z^{j}} \end{equation} \]

Esta condición (\(| \omega_0^i - \omega_0^j | \gg 2 \pi |J_{ij}|\)) se cumple fácilmente para los espines heteronucleares y que también puede cumplirse para las moléculas homonucleares pequeñas. La interpretación del término de acoplamiento escalar de la Ec. (4.26) es que un espín “siente” un campo magnético estático a lo largo de \(\pm z\) producido por los espines vecinos, además del campo \(\vec{B}_0\) aplicado externamente. Este campo adicional desplaza los niveles de energía como podemos ver en la Fig. 4.5. Como resultado, la frecuencia de Larmor del espín \(i\) se mueve en una cantidad \(-J_{ij}/2\) si el espín \(j\) está en el estado \(\ket{0}\) (lineas rojas) y una cantidad \(+J_{ij}/2\) si está en el estado \(\ket{1}\) (líneas azules).

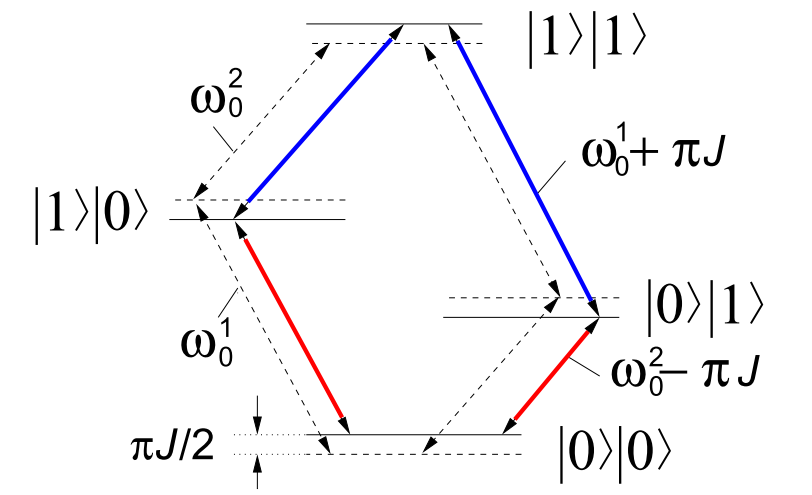
Fig. 4.5 Diagrama de niveles de energía para dos espines desacoplados (líneas discontinuas) y dos espines acoplados (líneas continuas) por un Hamiltoniano de la forma de la Ec. (4.26) (en unidades de \(\hbar\)). Marcadas en rojo están las dos transiciones en las que el espín que no cambia está en el estado \(\ket{0}\), mientras que en azul están en las que el espín que no cambia está en el estado \(\ket{1}\). Vemos que la energía de transición de las primera disminuye, mientras que de las segundas aumenta.#

4.3.1.3. Hamiltoniano completo.#

En resumen, la forma más simple del Hamiltoniano para un sistema de \(n\) espines nucleares acoplados es, pues (de las Ecs. (4.23) y (4.26))

(4.27)#\[\begin{equation} \boxed{\mathcal{H}_{sys} = - \sum_{i}^n \omega_0^i S_z^{i} + \frac{1}{\hbar} \sum_{i<j} 2 \pi J_{ij} S_z^i S_z^j} \end{equation} \]

4.3.2. Hamiltoniano de control#

4.3.2.1. Campos de radiofrecuencia#

Pasemos ahora a los mecanismos físicos para controlar el sistema de RMN. El estado de una partícula de espín \(1/2\) en un campo magnético estático \(\vec{B}_0\) a lo largo del eje \(\hat{z}\) puede manipularse aplicando un campo electromagnético \(\vec{B}_1(t)\) que gira en el plano \(\hat{x}-\hat{y}\) a frecuencia \(\omega_{rf}\), en o cerca de la frecuencia de precesión del espín \(\omega_0\). El Hamiltoniano de espín correspondiente al campo de radiofrecuencia (RF) es, análogo a la Ec. (4.13) para el campo estático \(B_0\),

(4.28)#\[\begin{equation} \mathcal{H}_{rf} = - \gamma B_1 \Lc \cos (\omega_{rf} + \phi) S_x + \sin (\omega_{rf} + \phi) S_y \Rc \, \end{equation}\]

donde \(\phi\) es la fase del campo de RF, y \(B_1\) su amplitud. Para \(n\) espines tenemos

(4.29)#\[\begin{equation} \boxed{\mathcal{H}_{rf} = - \sum_{i}^n \gamma_i B_1 \Lc \cos (\omega_{rf} t + \phi) S_x^i + \sin (\omega_{rf} t+ \phi ) S_y^i \Rc} \, , \end{equation} \]

Nota (implementación de un campo rotante en el laboratorio)

En la práctica, se aplica un campo magnético que oscila a lo largo de un eje fijo en el laboratorio, perpendicular al campo magnético estático. Este campo oscilante puede descomponerse en dos campos contrarrotatorios, uno de los cuales gira a \(\omega_{rf}\) en la misma dirección que el espín y, por tanto, puede establecerse en resonancia con el espín o cerca de ella. La otra componente gira en la dirección opuesta y, por lo tanto, está muy lejos de la resonancia (en aproximadamente \(2\omega_0\)). Como veremos, su único efecto es un desplazamiento insignificante de la frecuencia de Larmor, llamado desplazamiento Bloch-Siegert.

4.3.2.2. Sistema de referencia rotante (rotating frame).#

El movimiento de un espín nuclear individual sometido a un campo magnético estático y giratorio es bastante complejo cuando se describe en el sistema de coordenadas habitual del laboratorio (el marco del laboratorio). Sin embargo, se simplifica mucho describiendo el movimiento en un sistema de coordenadas que gira alrededor de \(\hat{z}\) a frecuencia \(\omega_{rf}\) (el rotating frame):

(4.30)#\[\begin{equation} \ket{\psi}^{rot} = \exp \lp -i \omega_{rf} t S_z/\hbar \rp \ket{\psi} \end{equation} \]

Para un solo espín libre, el Hamiltoniano será la suma (4.23) y (4.29) (con \(n=1\)), es decir,

(4.31)#\[\begin{equation} \mathcal{H} = - \omega_0 S_z - \omega_1 \Lc \cos (\omega_{rf} t+ \phi) S_x + \sin (\omega_{rf} t + \phi) S_y \Rc \end{equation} \]

Este Hamiltoniano junto con el estado en el sistema de referencia estático cumplen la ecuación de Schrödinger

(4.32)#\[\begin{equation} i \hbar \frac{d \ket{\psi}}{dt} = \mathcal{H} \ket{\psi} \end{equation}\]

Sustituyendo el cambio de variable de la Ec. (4.27) en la ecuación de Schrödinger, podemos calcular como tendría que ser el \(\mathcal{H}^{rot}\) que cumpla

(4.33)#\[\begin{equation} i \hbar \frac{d \ket{\psi}^{rot}}{dt} = \mathcal{H}^{rot} \ket{\psi}^{rot} \end{equation}\]

Puede ver que el resultado es

(4.34)#\[\begin{equation} \boxed{\mathcal{H}^{rot} = - (\omega_0 - \omega_{rf}) S_z - \omega_1 \Lc \cos (\phi) S_x + \sin (\phi) S_y \Rc} \end{equation} \]

Naturalmente, el campo de RF se encuentra a lo largo de un eje fijo en el sistema de referencia que gira a \(\omega_{rf}\). El movimiento del espín visto desde un sistema de referencia o el otro es diferente.

En el sistema laboratorio (en reposo), al aplicar el campo magnético rotante \(\vec{B}_1\) lo que sucede es que el valor esperado del espín rota en espiral, bajando por la esfera, como podemos ver en la Fig. 4.6b.

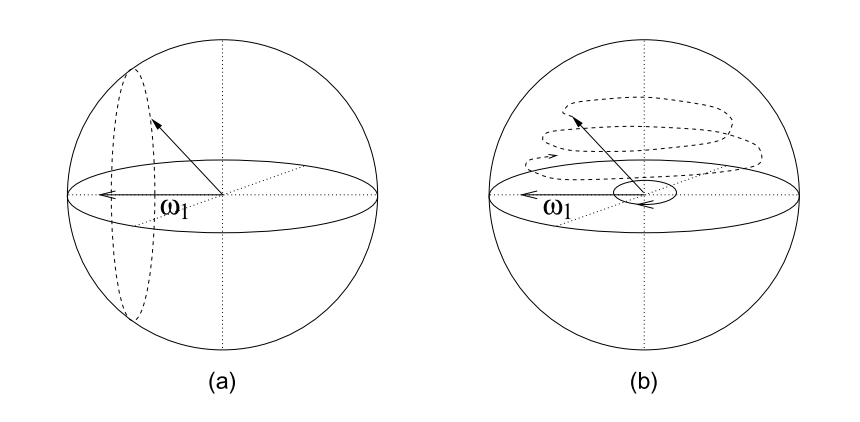
Fig. 4.6 Nutación de un espín sometido a un campo de RF transversal observada en el marco de rotación (a) y observada en el marco de laboratorio (b).#
En el sistema rotante, tenemos dos casos:
- Caso resonante (\(\omega_{rf} = \omega_0\)): en este caso el primer término de la Ec. (4.34) desaparece. En este caso, un observador en el sistema rotante verá el espín simplemente precesar alrededor de \(\vec{B}_1\) (Fig. 4.6a), un movimiento llamado nutación. La elección de \(\phi\) controla el eje de nutación.
- Caso fuera de resonancia: Si el campo de RF está fuera de resonancia con respecto a la frecuencia de espín en \(\Delta \omega = \omega_0 - \omega_{rf}\), el espín precesa en el marco de rotación alrededor de un eje inclinado con respecto al eje \(\vec{z}\) en un ángulo
  
  (4.35)#\[\begin{equation} \alpha = \arctan (\omega_1 / \Delta \omega) \end{equation}\]
  
  como se ilustra en la Fig. 4.7.
  
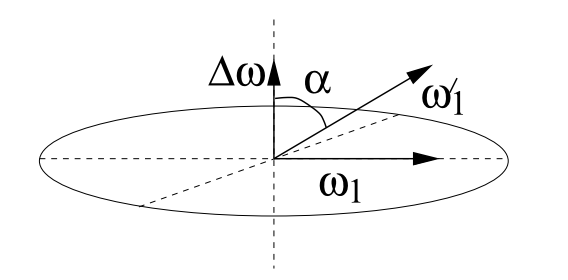
  Fig. 4.7 Eje de rotación (en el marco giratorio) durante un pulso de radiofrecuencia fuera de resonancia.#

En este último caso se deduce que el campo de RF no tiene prácticamente ningún efecto sobre espines que están lejos de la resonancia, ya que \(\alpha\) es muy pequeño cuando \(|\Delta \omega | \gg \omega_1\) (ver Fig. 4.8). Si todos los espines tienen frecuencias de Larmor bien separadas, en principio podemos rotar selectivamente cualquier qubit sin rotar los otros espines.

Los pulsos moderadamente fuera de resonancia (\(|\Delta \omega| \approx \omega_1\)) hacen girar el espín, pero debido a la inclinación del eje de rotación, un solo pulso de este tipo no puede, por ejemplo, voltear un espín de \(|0 \rangle\) a \(|1 \rangle\) (véase de nuevo la Fig. 4.8). Por supuesto, los pulsos fuera de resonancia también pueden ser útiles, por ejemplo para la implementación directa de rotaciones sobre un eje fuera del plano \(\hat{x} - \hat{y}\).

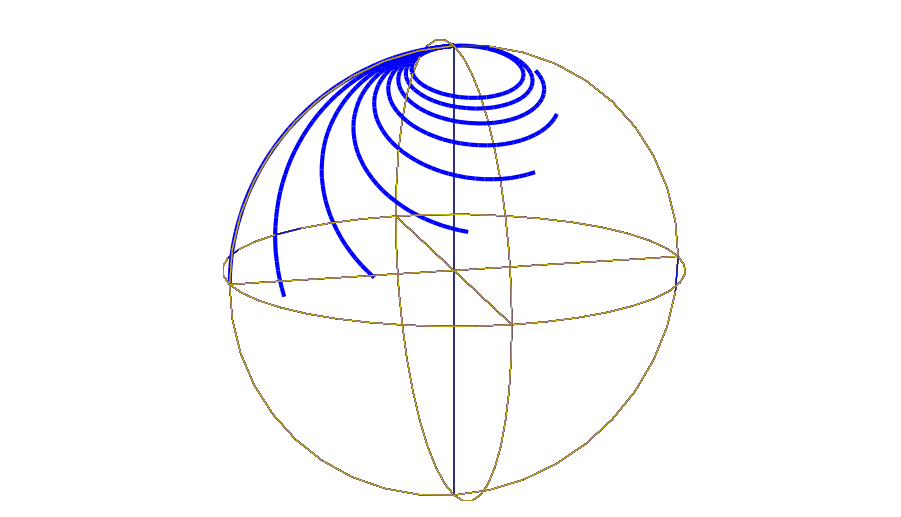
../../../_images/Fig_Harware_NMR_espiral_bloch_2.png — Fig. 4.8 Trayectoria en la esfera de Bloch (en el sistema de referencia rotante) descrita por un qubit inicialmente en \(\ket{0}\) (a lo largo de \(+\hat{z}\)), después de aplicar un pulso de 250 \(\mu s\) de intensidad \(\omega_1 = 1\) kHz fuera de resonancia en \(0\), \(0.5\), \(1\), \(\dots\) 4 kHz. En resonancia, el pulso produce una rotación \(90º\). Lejos de la resonancia, el qubit apenas rota alejándose de \(\ket{0}\).#

Por otro lado, podemos elegir trabajar en un sistema de referencia que rote a \(\bm{\omega_0}\) (en vez de a \(\omega_{rf}\), donde

(4.36)#\[\begin{equation} \boxed{\mathcal{H}^{rot} = - \omega_1 \Lc \cos ((\omega_{rf} - \omega_0)t + \phi) S_x + \sin ((\omega_{rf} - \omega_0)t + \phi) S_y \Rc} \end{equation}\]

Esta transformación no da un Hamiltoniano de RF independiente del tiempo (a menos que \(\omega_{rf} = \omega_0\)), como fue el caso para \(\mathcal{H}^{rot}\) en la Ec. (4.34)). Sin embargo, es un punto de partida natural para la extensión al caso de múltiples espines, donde puede introducirse un marco de rotación separado para cada espín:

(4.37)#\[\begin{equation} \ket{\psi}^{rot} = \Lc \prod_i \exp (-i \omega_0^i t S^i_z/\hbar ) \Rc \ket{\psi} \end{equation} \]

En presencia de múltiples campos de RF indexados con \(r\), el Hamiltoniano en este marco de referencia rotante e \(\omega_0\) nos queda

(4.38)#\[\begin{equation} \boxed{\mathcal{H}^{rot} = \sum_{i,r} - \omega_1^r \Lc \cos ((\omega_{rf}^r - \omega_0^i)t + \phi^r) S_x^i + \sin ((\omega_{rf}^r - \omega_0^i) t +\phi^r) S_y^i \Rc} \end{equation}\]

donde las amplitudes \(\omega_i^r\) y las fases \(\phi^r\) están bajo control.

El Hamiltoniano del sistema de la Ec. (4.27) se simplifica en el sistema de referencia multi-rotante de la Ec. (4.37): el termino \(S_z^i\) desparece dejando solo el término de acoplamiento \(J_{ij} S_z^i S_z^j\), que permanecen invariantes.

En resumen, en el sistema de referencia multi-rotante, el Hamiltoniano de \(NMR\) \(\mathcal{H} = \mathcal{H}_{sys} + \mathcal{H}_{control}\) toma la forma

(4.39)#\[\begin{split}\begin{equation} \begin{aligned} & ~~~~ \boxed{ \mathcal{H}_{sys} = \, \frac{1}{\hbar} \sum_{i<j} 2 \pi J_{ij} S_z^i S_z^j} \\ &\boxed{\mathcal{H}_{control} = \, \sum_{i,j} - \omega_1^r \Lc \cos ((\omega_{rf}^r - \omega_0^i)t +\phi^r) S_x^i + \sin ((\omega_{rf}^r-\omega_0^i)t +\phi^r) S^i_y \Rc} \end{aligned} \end{equation} \end{split}\]

Autor:

David Castaño (UMA-SCBI)

License: Licencia Creative Commons Atribución-CompartirIgual 4.0 Internacional.

This work has been financially supported by the Ministry for Digital Transformation and of Civil Service of the Spanish Government through the QUANTUM ENIA project call - Quantum Spain project, and by the European Union through the Recovery, Transformation and Resilience Plan - NextGenerationEU within the framework of the Digital Spain 2026 Agenda.