Jun 03, 2025 | 4 min read
\( \newcommand{\bra}[1]{\langle #1|} \) \( \newcommand{\ket}[1]{|#1\rangle} \) \( \newcommand{\branew}[1]{\langle #1|} \) \( \newcommand{\ketnew}[1]{\langle #1|} \) \( \newcommand{\braket}[2]{\langle #1|#2\rangle} \) \( \newcommand{\ketbra}[2]{| #1\rangle \langle #2 |} \) \( \newcommand{\i}{{\color{blue} i}} \) \( \newcommand{\Hil}{{\cal H}} \) \( \newcommand{\cg}[1]{{\rm C}#1} \) \( \newcommand{\lp}{\left(} \) \( \newcommand{\rp}{\right)} \) \( \newcommand{\lc}{\left[} \) \( \newcommand{\rc}{\right]} \) \( \newcommand{\lch}{\left\{} \) \( \newcommand{\rch}{\right\}} \) \( \newcommand{\Lp}{\Bigl(} \) \( \newcommand{\Rp}{\Bigr)} \) \( \newcommand{\Lc}{\Bigl[} \) \( \newcommand{\Rc}{\Bigr]} \) \( \newcommand{\Lch}{\Bigl\{} \) \( \newcommand{\Rch}{\Bigr\}} \) \( \newcommand{\rqa}{\quad \Rightarrow \quad} \) \( \newcommand{\bm}{\boldsymbol}\)
2.2. Trampas de iones#
Un ion fotoionizado recién nacido tiene típicamente una energía de \(\sim\)1 keV, lo que corresponde a una velocidad de \(\sim\)1 m s\({}^{-1}\) para un ion como el 40Ca\({}^+\). A tales energías, el ion puede considerarse un sistema clásico desde el punto de vista del movimiento. Por tanto, para construir un sistema completamente cuántico necesitamos restringir su movimiento tanto en el espacio (atraparlo) como en velocidad (enfriarlo).
Una trampa de iones es un dispositivo cuya finalidad es mantener los iones confinados en una estrecha región del espacio. Una condición necesaria para que esto ocurra es que el ion sienta un mínimo de la energía potencial \(V(x)\) (el centro de la trampa) en algún punto dentro de la región de atrapamiento.
Nota (Energía potencial)
Una buena forma de explicar los mínimos de la energía potencial es usando la energía potencial gravitatoria, es decir, la generada por la fuerza de la gravedad.
En el caso de la energía potencial gravitatoria, esta crece a medida que nos alejamos del centro de la Tierra. Es decir, una pelota en lo alto de un edificio tiene más energía potencial gravitatoria que a la altura de la calle. Por ese motivo, si soltamos la pelota desde lo alto, esta caerá (hacía la zona con menos energía potencial). A medida que vaya cayendo, la pelota perderá energía potencial y ganará energía cinética (velocidad), conservándose la cantidad total de energía.
El resumen es que, cuando tenemos una fuerza central (como la gravitatoria o la eléctrica) esta trae consigo un potencial. Los objetos que sienten estas fuerzas se mueven hacia zonas de menos potencial.
Aprovechando la naturaleza cargada de los iones, se puede crear un potencial de atrapamiento utilizando una combinación adecuada de potenciales eléctricos y/o magnéticos. Existen dos paradigmas para el diseño de dicho potencial de atrapamiento:
La trampa de Penning, en la que se utilizan potenciales eléctricos y magnéticos estáticos.
La trampa de Paul, en la que se utilizan campos eléctricos estáticos y oscilantes.
Aunque ambos son en principio adecuados para aplicaciones de computación cuántica, la trampa de Paul es actualmente el método más utilizado en entornos académicos e industriales.
Suficientemente cerca del centro de la trampa (del mínimo del potencial), cualquier potencial puede aproximarse bien mediante una función cuadrática de las coordenadas, es decir, un ion atrapado se comportará como un oscilador armónico simple (SHO) en tres dimensiones.
Los sistemas de captura más utilizados en aplicaciones de computación cuántica son las trampas lineales: la fuerza de captura en dos de las tres dimensiones es mucho mayor que la de la tercera (por ejemplo, una trampa Paul muy fuerte en las direcciones \(x\) e \(y\) y un par de electrodos relativamente más débiles en la dirección \(z\), como en la Fig. 2.1), por lo que el único movimiento relevante será un movimiento armónico simple en (digamos) la dirección \(\hat{z}\), caracterizado por una frecuencia \(\omega_z\) y por la masa \(M\) del ion.
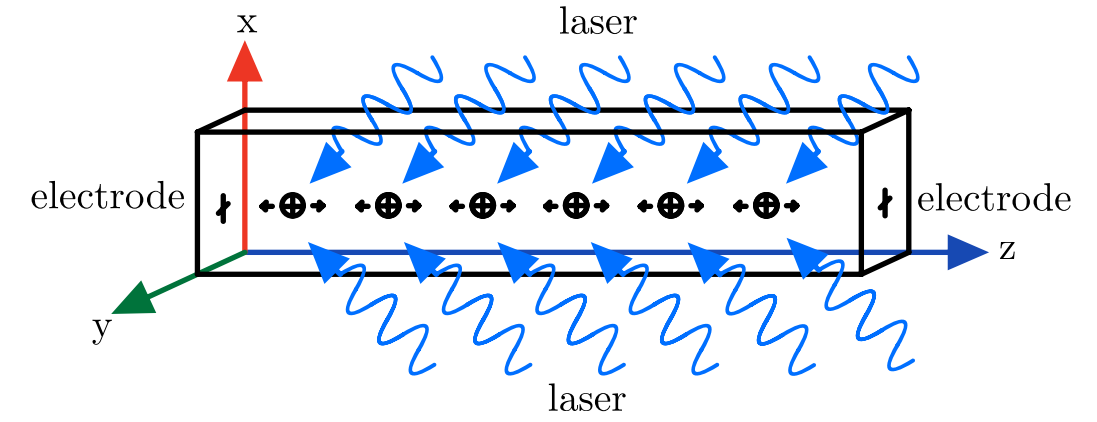
Fig. 2.1 Iones fuertemente atrapados por una trampa Paul en el plano \(xy\), y a los que sólo se permite moverse en la dirección \(z\). Un par de electrodos impiden que los iones se repelan fuera de la trampa. Fuente [3].#
Para que la aproximación armónica se mantenga, el ion no debe alejarse apreciablemente del centro de la trampa. Si esto ocurre, ya no podemos garantizar que las fuerzas que actúan sobre el ion se dirijan hacia el centro de la trampa, y en algún momento podríamos incluso hallarlo fuera de la trampa.
Por la razón anterior, es importante que el ion se mueva lentamente, por lo que queremos disminuir su energía cinética. Con un ligero abuso del lenguaje llamamos a esta etapa “enfriamiento” asociando una temperatura a la energía cinética, aunque el ion no esté en equilibrio térmico. En la sección 2.3 describiremos dos ejemplos de enfriamiento por láser, válidos en los regímenes clásico y cuántico, respectivamente. Utilizando láseres convenientemente sintonizados, es posible impartir una fuerza de amortiguación efectiva sobre los iones, que los ralentiza.
Por último, las colisiones con otras partículas también son perjudiciales para el procedimiento de atrapamiento, ya que pueden inducir cambios bruscos en la energía cinética, lo que puede provocar el escape de iones de la trampa. Para minimizar tales interacciones, se crea un vacío ultraalto a presiones de unos \(10^{-11}\) Torr (\(\sim 1,3 \times 10^{-9}\) Pa) en la región donde se colocará la trampa.
Autor:
David Castaño (UMA-SCBI)



License: Licencia Creative Commons Atribución-CompartirIgual 4.0 Internacional.
This work has been financially supported by the Ministry for Digital Transformation and of Civil Service of the Spanish Government through the QUANTUM ENIA project call - Quantum Spain project, and by the European Union through the Recovery, Transformation and Resilience Plan - NextGenerationEU within the framework of the Digital Spain 2026 Agenda.

