Jun 03, 2025 | 12 min read

Volver a TalentQ

\( \newcommand{\bra}[1]{\langle #1|} \) \( \newcommand{\ket}[1]{|#1\rangle} \) \( \newcommand{\branew}[1]{\langle #1|} \) \( \newcommand{\ketnew}[1]{\langle #1|} \) \( \newcommand{\braket}[2]{\langle #1|#2\rangle} \) \( \newcommand{\ketbra}[2]{| #1\rangle \langle #2 |} \) \( \newcommand{\i}{{\color{blue} i}} \) \( \newcommand{\Hil}{{\cal H}} \) \( \newcommand{\cg}[1]{{\rm C}#1} \) \( \newcommand{\lp}{\left(} \) \( \newcommand{\rp}{\right)} \) \( \newcommand{\lc}{\left[} \) \( \newcommand{\rc}{\right]} \) \( \newcommand{\lch}{\left\{} \) \( \newcommand{\rch}{\right\}} \) \( \newcommand{\Lp}{\Bigl(} \) \( \newcommand{\Rp}{\Bigr)} \) \( \newcommand{\Lc}{\Bigl[} \) \( \newcommand{\Rc}{\Bigr]} \) \( \newcommand{\Lch}{\Bigl\{} \) \( \newcommand{\Rch}{\Bigr\}} \) \( \newcommand{\rqa}{\quad \Rightarrow \quad} \) \( \newcommand{\bm}{\boldsymbol}\)

3.8. Puertas simples

En esta sección, revisaremos los pasos necesarios para demostrar que el acoplamiento capacitivo de microondas a un circuito superconductor puede utilizarse para accionar puertas de un solo qubit. Para ello, consideraremos el acoplamiento de un qubit superconductor a una fuente de microondas (a veces denominado “qubit drive”) como se muestra en la Fig. 3.15. Un análisis completo del circuito de la Fig. 3.15 está fuera del alcance de esta revisión, por lo que aquí nos conformamos con resaltar los pasos que elucidan la física del acoplamiento de la fuente con el qubit.

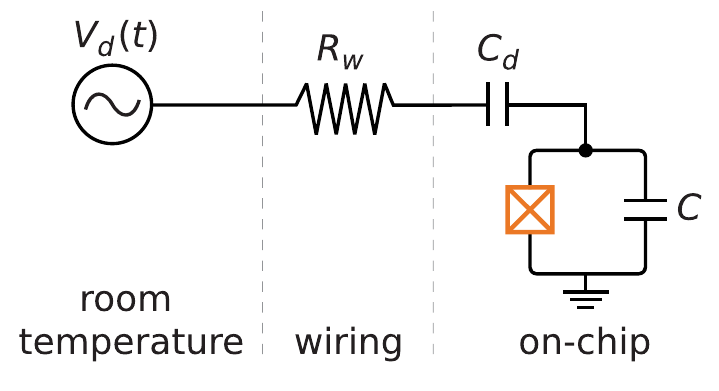
Fig. 3.15 Diagrama del circuito de acoplamiento capacitivo de una línea de accionamiento de microondas (microwave drive line) [caracterizada por un voltaje \(V_d(t)\) dependiente del tiempo] a un qubit superconductor transmónico genérico. Figura tomada de [16]

3.8.1. Acoplamiento capacitivo para las puertas \(X\) e \(Y\)

3.8.1.1. Modelado del circuito de la Fig. 3.15.

Comenzamos modelando el qubit como un oscilador armónico, para el que el Hamiltoniano del circuito (clásico) puede calcularse mediante técnicas de cuantización de circuitos, partiendo de las leyes de Kirchoffs (no lo veremos en detalle), y viene dado por

(3.114)\[\begin{equation} H = \frac{\tilde{Q}(t)^2}{2 C_\varSigma} + \frac{\Phi^2}{2L} + \frac{C_d}{C_\varSigma} V_d(t) \tilde{Q} \end{equation}\]

con

(3.115)\[\begin{equation} C_{\varSigma} = C + C_d \qquad , \qquad \tilde{Q} = C_\varSigma \dot{\Phi} - C_d V_d(t) \end{equation}\]

donde \(C_\varSigma\) capacitancia total a tierra y \(\tilde{Q}\) es una variable de carga renormalizada para el circuito. Ahora podemos promover las variables de flujo y carga a operadores cuánticos y suponer un acoplamiento débil a la linea de control (“drive line”), de modo que

(3.116)\[\begin{equation} \tilde{Q} \approx \hat{Q}\,, \end{equation}\]

y llegamos a

(3.117)\[\begin{equation} H = H_{LC} + \frac{C_d}{C_\varSigma} V_d(t) \hat{Q} \end{equation}\]

donde \(H_{LC}\) es la forma de ls Ec. (3.79) y hemos mantenido sólo los términos que se acoplan a las variables dinámicas. Siguiendo un poco lo mismo que hicimos en la Ec. (3.87), podemos reescribir el operador de carga de la forma:

(3.118)\[\begin{equation} \hat{Q} = -i Q_{zpf} (a - a^\dagger) \end{equation}\]

donde \(Q_{zpf} = \sqrt{\hbar/2Z}\) es la fluctuación de carga de punto cero y \(Z=\sqrt{L/C}\) es la impedancia del circuito a tierra. Así, el oscilador LC acoplado capacitivamente a una “drive line” puede escribirse como

(3.119)\[\begin{equation} H = \hbar \omega \lp a^\dagger a + \frac{1}{2} \rp - \frac{C_d}{C_\varSigma} V_d(t) i Q_{zpf} (a-a^\dagger)\, , \end{equation} \]

donde vemos que el primer término es de la forma de la Ec. (3.59). Finalmente, truncando a la transición más baja del oscilador, podemos hacer la sustitución \(a \rightarrow \sigma^{-}\) y \(a^\dagger \rightarrow \sigma^{+}\) (ver las Ec. (3.98)) en todo y llegar a

(3.120)\[\begin{equation} H = - \underbrace{\frac{\hbar \omega_q}{2} \sigma_z}_{H_{\mathrm{TLS}}} + \underbrace{\Omega V_d (t) \sigma_y}_{H_d}\, \end{equation} \]

donde \(\Omega = (C_d/C_{\varSigma}) Q_{zpf}\), \(\omega_q = (E_1 - E_0)/\hbar\) y donde \(H_{TLS}\) es el hamiltoniano de un sistema de dos niveles (ver Ec. (3.97)). Nuevamente, al truncar y quedarnos con los dos niveles de menos energía estamos quedandonos con un TLS.

3.8.1.2. Imagen de rotación (o de interacción)

Para entender mejor la acción de la fuente sobre el circuito, vamos a movernos a la denominada imagen de rotación (“rotating frame” o “interacting frame”). En este caso no es nada más que un cambio de variables en el nos movemos a sistema de referencia que rota con el qubit a frecuencia \(\omega_q\). El operador de cambio de variable que nos lleva a este sistema de referencia es

(3.121)\[\begin{equation} U_{\mathrm{rf}} = e^{i H_0 t/\hbar} = U_{H_0}^\dagger \,. \end{equation} \]

Vemos que este operador es el hemítico conjugado del operador de evolución temporal para el Hamiltoniano \(H_0\). Los estados en este sistema de referencia toman la forma

(3.122)\[\begin{equation} \ket{\psi_{\mathrm{rf}}(t)} = U_{\mathrm{rf}} \ket{\psi_0} \, . \end{equation}\]

La evolución temporal en esta nueva imagen se obtiene de nuevo a partir de la ecuación de Schrödinger.

(3.123)\[\begin{split}\begin{equation} \begin{split} i \frac{\partial }{\partial t} \ket{\psi_{\mathrm{rf}}(t)} = i \frac{\partial }{\partial t} \lp U_{\mathrm{rf}} \ket{\psi_0} \rp & = i \lp \frac{\partial }{\partial t} U_{\mathrm{rf}} \rp \underbrace{\ket{\psi_0}}_{U_{\mathrm{rf}}^\dagger \ket{\psi_{\mathrm{rf}}}} + i U_{\mathrm{rf}} \underbrace{\lp \frac{\partial }{\partial t} \ket {\psi_0} \rp}_{H\ket{\psi_0}} \\ & = \underbrace{\lp i \dot{U}_{\mathrm{rf}} U_{\mathrm{rf}}^\dagger + U_{\mathrm{rf}} H U_{\mathrm{rf}}^\dagger \rp}_{\tilde{H}} \ket{\psi_{\mathrm{rf}}} \end{split} \end{equation} \end{split}\]

Podemos pensar en el término \(\tilde{H}\) en paréntesis en la Ec. (3.123) como la expresión de \(H\) en la imagen de rotación.

Si nos ponemos en el caso simple en que \(H = H_{TLS}\), podemos ver de forma simple que \(\tilde{H}_{TLS} = 0\) como se esperaba, pues la transformación de la Ec. (3.123) está pensada para eliminar la dependencia temporal en este caso.

Volviendo a la Ec. (3.120), vemos que el Hamiltoniano en la imagen de rotación nos queda:

(3.124)\[\begin{equation} \tilde{H} = \tilde{H}_d = U_{\mathrm{rf}} H_d U_{\mathrm{rf}}^\dagger \end{equation} \]

Haciendo cálculos llegamos a

(3.125)\[\begin{equation} \tilde{H}_d = \Omega V_d(t) \lc \cos (\omega_q t)\sigma_y - \sin(\omega_q t) \sigma_x \rc \,. \end{equation} \]

Ejercicio

a) Verifica que \(\tilde{H}_{TLS} = 0\). b) Obtén la expresión de la Ec. (3.125). Para ello usa la Ec. (3.124), ten en cuanta la expresión de la exponencial de las metrices de Pauli y las expresiones del seno y el coseno del ángulo doble.

3.8.1.3. Componentes “in-phase” y “out-of-phase”.

En general, podemos suponer que la parte de la tensión que depende del tiempo \((V_d(t) = V_0 v(t))\) tiene una forma genérica

(3.126)\[\begin{equation} \begin{aligned} v(t) & = s(t) \sin (\omega_d t + \phi ) \\ & = s(t) (\cos (\phi) \sin (w_d t) + \sin (\phi) \cos (\omega_d t))\, , \end{aligned} \end{equation}\]

donde \(s(t)\) es una función adimensional denominada envolvente, de modo que la amplitud del impulso está fijada por \(V_0 s(t)\). (Puede verse más sobre modulación de señales en la Fig. 3.16). Adoptando las definiciones

(3.127)\[\begin{equation} \begin{aligned} I = & \cos (\phi) \qquad \text{(la componente "in-phase")} \, , \\ Q = & \sin (\phi) \qquad \text{(la componente "out-of-phase" o cuadratura)} \, , \end{aligned} \end{equation}\]

el Hamiltoniano de control en el marco de rotación toma la forma

(3.128)\[\begin{split}\begin{equation} \begin{aligned} \tilde{H}_d = & \Omega V_0 s(t) \lc I \sin (\omega_d t) + Q \cos (\omega_d t) \rc \\ & \times \lc \cos (\omega_q t)\sigma_y - \sin(\omega_qt) \sigma_x \rc \end{aligned} \end{equation} \end{split}\]

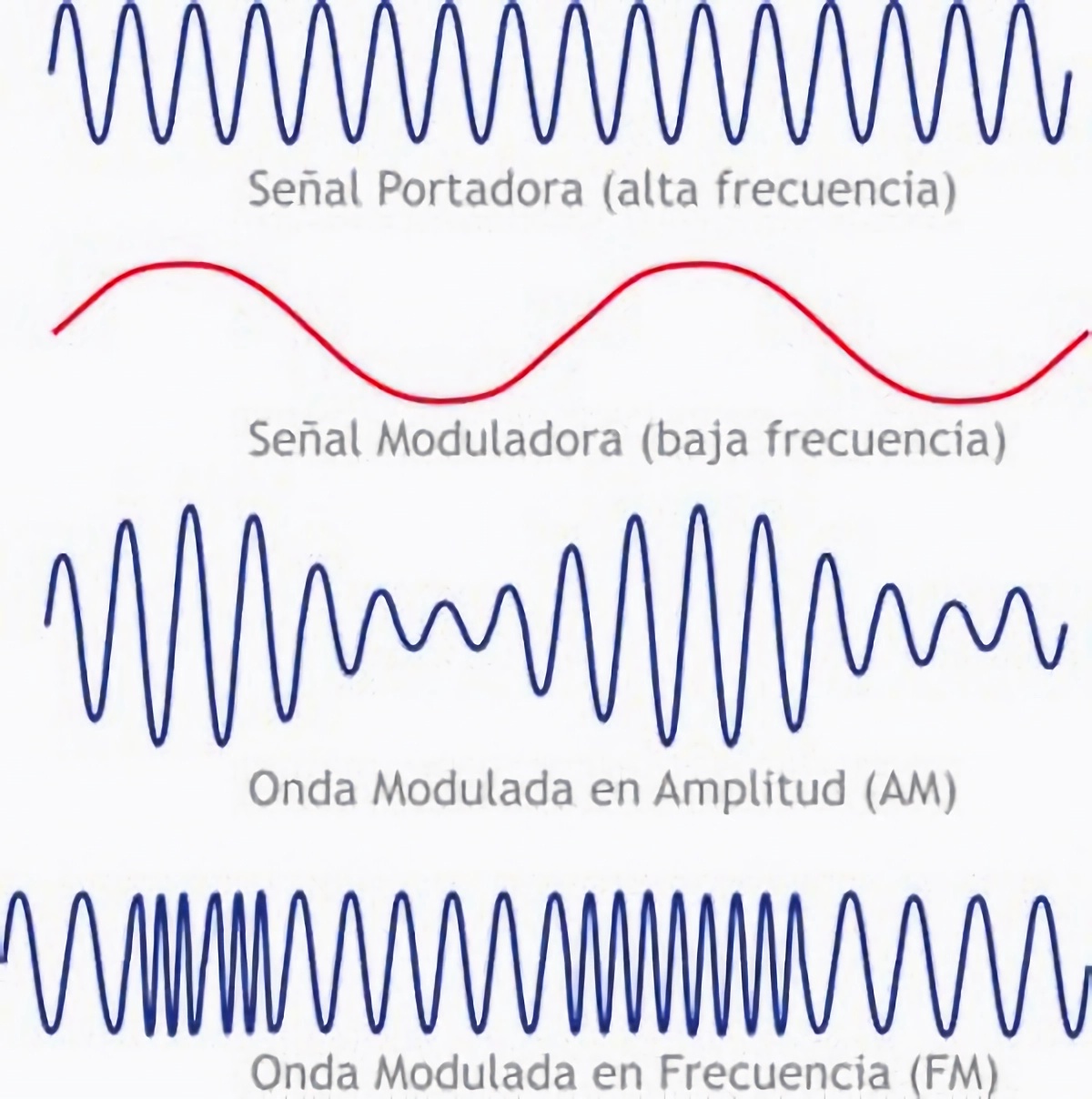
Fig. 3.16 Ejemplos de ondas moduladas, tanto en amplitud (lo que se usa en control de qubits y en la radio AM), como en frecuencia (lo que usa en las radios FM). Como vemos tenemos dos ondas, la portadora y la moduladora. La gracia aquí es que la información que se quiere transmitir está en la onda moduladora. Esta puede ser, por ejemplo, la onda del sonido que tiene que emitir la rádio del coche. La onda portadora se usa para transmitir la información de la moduladora.

Nota (errata en [89]

Haciendo cálculos, llego a la conclusión de que en el paper [16] hay algunas inconsistencias con los signos. Se invita al lector a repasar la veracidad de los mismos.

Vamos a reescribir la Ec. (3.128):

(3.129)\[\begin{split}\begin{equation} \begin{aligned} \tilde{H}_d = \Omega V_0 s(t) & [ (- I \sin (\omega_d t)\sin(\omega_qt) - Q \cos (\omega_d t)\sin(\omega_qt)) \sigma_x\\ & + (I \sin (\omega_d t)\cos (\omega_q t) + Q \cos (\omega_d t)\cos (\omega_q t) ) \sigma_y ] \end{aligned} \end{equation} \end{split}\]

Nota (relaciones trigonométricas del ángulo suma y resta)

Tenemos las dos relaciones:

(3.130)\[\begin{equation} \begin{aligned} \sin(x\pm y) &= \sin(x)\cos(y) \pm \cos(x)\sin(y) \\ \cos(x \pm y) &= \cos(x) \cos(y) \mp \sin(x) \sin(y) \end{aligned} \end{equation}\]

de las cuales podemos deducir:

(3.131)\[\begin{split}\begin{equation} \begin{aligned} 2 \sin(x)\cos(y) &= \sin(x + y) + \sin(x - y) \\ 2 \cos(x)\sin(y) &= \sin(x + y) - \sin(x - y) \\ 2 \cos(x)\cos(y) &= \cos(x + y) + \cos(x - y) \\ 2 \sin(x)\sin(y) &= \cos(x - y) - \cos(x + y) \end{aligned} \end{equation} \end{split}\]

Usando las relaciones de la Ec. (3.131), podemos reescribir la Ec. (3.129)

(3.132)\[\begin{split}\begin{equation} \begin{aligned} \tilde{H}_d = \frac{1}{2} \Omega V_0 s(t) & [ (- I \cos((\omega_d - \omega_q)t) + Q \sin((\omega_d - \omega_q)t)) \sigma_x \\ & + (I \sin((\omega_d - \omega_q)t) + Q \cos((\omega_d - \omega_q)t)) \sigma_y ] \end{aligned} \end{equation} \end{split}\]

donde se han despreciado los términos de rotación rápida que promediarán a cero (es decir, términos con \(\omega_d + \omega_q\)), conocida como aproximación de onda rotatoria (RWA). Tomando \(\delta \omega = \omega_q - \omega_d\) llegamos a

(3.133)\[\begin{split}\begin{equation} \begin{aligned} \tilde{H}_d = \frac{1}{2} \Omega V_0 s(t) & [(-I \cos(\delta \omega t) - Q \sin(\delta \omega t)) \sigma_x \\ & + (- I \sin(\delta \omega t) + Q \cos(\delta \omega t)) \sigma_y ] \end{aligned} \end{equation} \end{split}\]

Como ejemplo concreto, supongamos que aplicamos un pulso a la frecuencia del qubit, de forma que \(\delta \omega = 0\), entonces

(3.134)\[\begin{equation} \tilde{H}_d = - \frac{\Omega}{2} V_0 s(t) (I \sigma_x - Q \sigma_y) \end{equation}\]

mostrando que un pulso “en fase” (\( \phi = 0\), es decir, el componente \(I\)) corresponde a rotaciones alrededor del eje \(x\), mientras que un pulso fuera de fase (\(\phi = \pi/2\), es decir, el componente \(Q\)), corresponde a rotaciones alrededor del eje \(y\).

3.8.1.4. Ejemplo de pulso “in-phase”.

Como ejemplo concreto de pulso en fase, si se escribe el operador unitario se obtiene

(3.135)\[\begin{equation} U_{\mathrm{rf,d}}^{\phi = 0} = \exp \lp \lc \frac{i}{2} \Omega V_0 \int_0^t s(t') dt' \rc \sigma_x \rp \end{equation} \]

que depende únicamente de los parámetros macroscópicos de diseño del circuito, así como de la envolvente del pulso \(s(t)\) y de la amplitud \(V_0\), que pueden controlarse utilizando generadores de forma de onda arbitraria (AWG). La ecuación se conoce como “Rabi driving”. Definimos

(3.136)\[\begin{equation} \Theta(t) = - \Omega V_0 \int_0^t s(t') dt'\,, \end{equation}\]

que es el ángulo de rotación de un estado dados los acoplamientos capacitivos, la impedancia del circuito, la magnitud \(V_0\) y la forma de onda envolvente, \(s(t)\). Esto significa que para implementar un pulso \(\pi\) en el eje \(x\), habría que resolver la ecuación \(\Theta (t) = \pi\) y emitir la senal “in-phase” correspondiente. En este lenguaje, una secuencia de pulsos [ver Fig. 3.17(a)] \(\Theta_k\), \(\Theta_{k-1}\), \(\dots \Theta_0\) se convierte en una secuencia de puertas operando sobre un qubit como

(3.137)\[\begin{equation} U_k U_{k-1} \cdots U_0 = \mathcal{T} \prod_{n=0}^k e^{- \frac{i}{2} \Theta_n(t) (I_n \sigma_x - Q_n \sigma_y)} \, , \end{equation} \]

donde \(\mathcal{T}\) es un operador que garantiza que los impulsos se generan en la secuencia ordenada en el tiempo correspondiente a \(U_k U_{k-1} \cdots U_0 \).

En la Fig. 3.17 se esboza la configuración típica de modulación en fase y cuadratura (IQ) utilizada para generar los pulsos. La Figura 3.17(a) muestra como un pulso a frecuencia \(\omega_d\) es generado usando un generador de microondas de bajo ruido de fase [típicamente denotado “oscilador local (LO)”], mientras que el pulso es formado combinando la señal LO en un mezclador IQ con pulsos generados en un AWG. Para permitir la multiplexación de frecuencias, la señal AWG se generará normalmente con un componente de baja frecuencia, \(\omega_{\mathrm{AWG}}\), de forma que la señal del LO se desplazará tal que \(\omega_{LO} + \omega_{AWS} = \omega_d\). Mezclando en más de una frecuencia \(\omega_{\mathrm{AWG1}}\), \(\omega_{\mathrm{AWG2}}\), … es posible abordar múltiples qubits (o resonadores de lectura) simultáneamente, mediante la superposición de controles individuales.

En la Fig. 3.17(b) mostramos esquemáticamente la comparación entre las puertas \(XY\) en un circuito cuántico y las formas de onda correspondientes generadas en el AWG (omitiendo para mayor claridad el componente de frecuencia \(\omega_{AWG}\)).

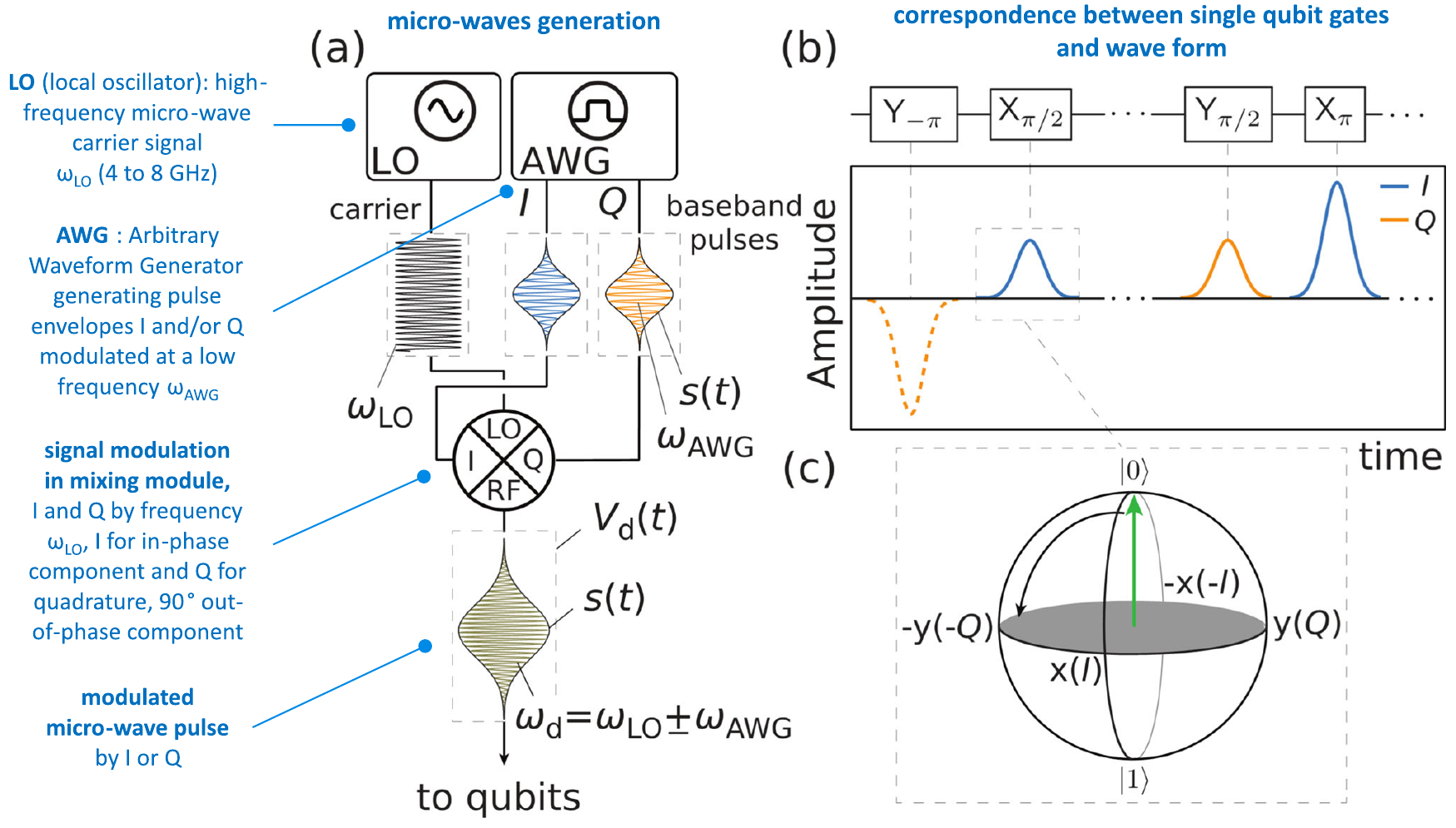
Fig. 3.17 a) Esquema de una configuración típica de control de un qubits. Una fuente de microondas suministra una señal de alta frecuencia (\(\omega_{LO}\)), mientras que un generador de onda arbitrarios (AWG de sus siglas en inglés) suministra una envolvente del pulso (\(s(t)\)), a veces con un componente de baja frecuencia, \(\omega_{AWG}\). El mezclador \(IQ\) combina las dos señales para generar una forma de onda \(V_d(t)\) con una frecuencia \(\omega_d = \omega_{LO} \pm \omega_{AWG}\), normalmente resonante con el qubit. b) Ejemplo de cómo una secuencia de puerta se traduce en una forma de onda generada por el AWG. Los colores indican los componentes \(I\) y \(Q\). c) La acción de un pulso \(X_{\pi/2}\) sobre un estado \(\ket{0}\) para producir el estado \(\ket{-i} = \frac{1}{\sqrt{2}} (\ket{0} - i\ket{1})\). Figura tomada de [6]

Nota (resumen)

Si nos fiamos podemos ver que la conclusión es la siguiente: la amplitud del pulso de microondas controla el ángulo de rotación y su fase el eje de rotación. Esto se traduce en que la fase \(\phi\) que ajustamos con las ondas \(IQ\) controla el eje, mientras que la envolvente \(s(t)\) que aplicamos al pulso controla la rotación.

3.8.2. Puerta \(Z\) virtual

Como vimos en la Sección %s, la distinción entre las rotaciones \(x\) e \(y\) no es más que una elección de fase en las señales de microondas, y el ángulo a rotar viene dado por \(\Theta (t)\), ambas generadas mediante un AWG. Dado que la elección de la fase \(\phi\) tiene un punto de partida arbitrario, podríamos considerar \(\phi \rightarrow \phi + \pi/2\). Esto daría lugar a \(I \rightarrow Q\) y \(Q \rightarrow -I\). Por lo tanto, al cambiar la fase, las rotaciones alrededor de \(x\) se convierten en rotaciones alrededor de \(y\) (y viceversa, con un cambio de signo). Esto recuerda al resultado de aplicar una rotación \(Z_{\pi}\), donde

(3.138)\[\begin{equation} Z_{\pi} X_{\pi} = i Y_{\pi} \qquad , \qquad Z_{\pi} Y_{\pi} = -i X_{\pi} \end{equation}\]

Nota

Véase que a lo que llamamos puertas \(X\), \(Y\) e \(Z\), son rotaciones de ángulo \(\pi\), con lo que \(X = X_{\pi}\), \(Y = Y_{\pi}\) e \(Z = Z_{\pi}\).

Esta analogía entre el cambio de fase de una señal generada por AWG y la aplicación de rotaciones \(Z\) puede utilizarse para implementar puertas \(Z\) “virtuales”. Esta intuición puede formalizarse mediante el siguiente ejemplo: consideremos el caso de aplicar un pulso con un ángulo \(\theta\) en el canal \(I\) (es decir, un \(X_\theta\)) seguido de otro pulso \(\theta\) en el canal \(I\), pero con una fase \(\phi_\theta\) respecto al primer pulso (denotado \(X_\theta^{(\phi_0)}\), donde \(X\) indica que seguimos utilizando el canal \(I\), pero el eje de rotación está ahora a un ángulo \(\phi_0\) del eje \(x\)). Usando la Ec. (3.137) corresponde a una secuencia de pulsos

(3.139)\[\begin{split}\begin{equation} \begin{aligned} X_\theta^{(\phi_0)} X_\theta & = e^{-i \frac{\theta}{2} \lp \cos(\phi_0) \sigma_x - \sin(\phi_0) \sigma_y \rp } X_\theta \\ & = Z_{-\phi_0} X_\theta Z_{\phi_0} X_\theta \, , \end{aligned} \end{equation} \end{split}\]

de donde vemos que el efecto de la fase \(\phi_0\) es aplicar \(Z_{\phi_0}\). El \(Z_{-\phi_0}\) final se debe a que la rotación se produce en el marco de referencia del qubit. Sin embargo, dado que la lectura se realiza a lo largo del eje \(z\), una rotación de fase final alrededor de \(z\) no cambiará el resultado de la medición. Por lo tanto, si se desea implementar la secuencia de puerta de la Fig. 3.18

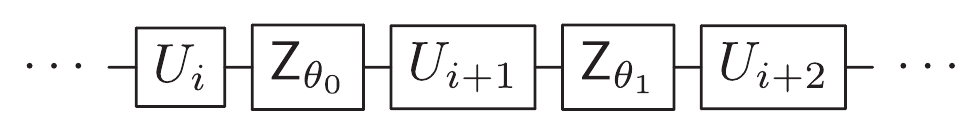
Fig. 3.18 Ejemplo de secuencia de puertas donde se incluyen puertas \(Z\). Figura tomada de [18].

donde las \(U_i\)’s son puertas arbitrarias, esto se puede hacer mediante la revisión de la secuencia de puertas (en el software de control para el AWG) y el cambio de la fase de los pulsos posteriores. El resultado lo vemos en la Fig. 3.19

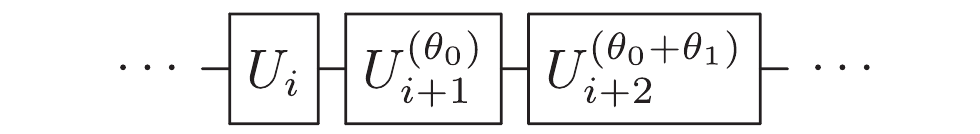
Fig. 3.19 Ejemplo de secuencia de puertas donde se han absorbido las puertas \(Z\) de la Fig. 3.18 como fases en las otras puertas. Figura tomada de [18].

lo que reduce el número total de puertas. Además, las puertas virtuales-Z son “perfectas”, en el sentido de que no requieren pulsos adicionales, y la puerta tarda “tiempo cero”, por lo que la fidelidad de la compuerta es nominalmente unidad.

Ejercicio

Verifica la veracidad de la Ec. (3.139). Es decir, comprueba que

(3.140)\[\begin{equation} Z_{-\phi_0} X_\theta Z_{\phi_0} = e^{-i \frac{\theta}{2} \lp \cos(\phi_0) \sigma_x - \sin(\phi_0) \sigma_y \rp} \end{equation}\]

Para ello ten en cuenta que (ver Ec. %s y Ec. %s)

(3.141)\[\begin{equation} \begin{aligned} X_\theta & = e^{-i \frac{\theta}{2} \sigma_x} = \mathbb{I} \cos \lp \frac{\theta}{2} \rp -i \sigma_x \sin \lp \frac{\theta}{2} \rp \\ Z_\theta & = e^{-i \frac{\theta}{2} \sigma_z} = \mathbb{I} \cos \lp \frac{\theta}{2} \rp -i \sigma_z \sin \lp \frac{\theta}{2} \rp \end{aligned} \end{equation}\]

No desarrolles las matrices!!! Trabaja con las matrices de Pauli y sus propiedades de multiplicación (ver Ec. %s).

(3.142)\[\begin{equation} \sigma_i \sigma_j = \delta_{ij} I + i \sum_{k=1}^3 \varepsilon_{ijk} \sigma_k, \qquad \qquad \left\{ \begin{aligned} &\varepsilon_{123}=\varepsilon_{231}=\varepsilon_{312} = 1 \\ &\varepsilon_{213}=\varepsilon_{132}=\varepsilon_{312} = -1 \\ &\text{y el resto cero} \end{aligned} \right. \end{equation}\]

Por último, mencionamos una característica más destacada de las puertas virtuales \(Z\): cualquier operación de un solo qubit (salvo una fase global) puede escribirse como

(3.143)\[\begin{equation} U (\theta, \phi, \lambda) = Z_{\phi - \frac{\pi}{2}} X_{\frac{\pi}{2}} Z_{\pi - \theta} X_{\frac{\pi}{2}} Z_{\lambda - \frac{\pi}{2}} \, , \end{equation} \]

para una elección adecuada de los ángulos \(\theta, \phi, \lambda\). Esto significa que el acceso a una única \(X_{\frac{\pi}{2}}\) físico combinado con la \(Z\) virtual da acceso a un conjunto completo de puertas de un solo qubit! Un ejemplo explícito de la Ec. (3.143) en acción es la puerta Hadamard, que puede escribirse como \(H = Z_{\pi/2} X_{\pi/2} Z_{\pi/2}\), pero como las \(Z\)’s pueden ser virtuales, es posible implementar Hadamards como una operación efectiva de un solo pulso en qubits superconductores.

3.8.3. El sistema DRAG

Al pasar de la Ec. (3.119) a la Ec. (3.120), asumimos que podíamos ignorar los niveles superiores del qubit. Sin embargo, para qubits débilmente anarmónicos, como el transmón normal (ver Sección 3.4.6), esta suposición puede no estar justificada, ya que \(\omega_q^{1 \rightarrow 2}\) sólo difiere de \(\omega_q (=\omega_q^{0 \rightarrow 1}\)) por la anarmonicidad, \(\alpha = \omega_q^{1 \rightarrow 2} - \omega_q\) (ver Ec. (3.94)), que para este caso es negativa y suele estar en torno a 200 o 300 MHz.

Esta situación se esboza en las Figs. 3.20(a)- 3.20©, donde ilustramos cómo los pulsos gaussianos con desviaciones estándar \(\sigma = {1,2,5}\) ns tienen un contenido espectral que conduce a solapamientos no nulos con la frecuencia \(\omega_q^{1 \rightarrow 2} = \omega_q - |\alpha|\). Esto conduce a dos efectos perjudiciales: (1) errores de fuga que sacan al qubit del subespacio computacional, y (2) errores de fase.

El efecto 2 se produce porque la presencia del pulso provoca una repulsión entre los niveles \(\ket{1}\) y \(\ket{2}\), cambiando a su vez \(\omega_q^{0 \rightarrow 1}\) a medida que se aplica el pulso. Esto conduce a la acumulación de una fase relativa entre \(\ket{0}\) y \(\ket{1}\).

El procedimiento denominado DRAG (Derivative Reduction by Adiabatic Gate) trata de combatir estos dos efectos aplicando una señal adicional en la componente “out-of-phase”. El truco consiste en modificar la envolvente de la forma de onda \(s(t)\) según

(3.144)\[\begin{split}\begin{equation} s(t) \rightarrow s'(t) = \left\{ \begin{matrix} s(t) & \text{en} & I \\ \lambda \frac{\dot{s}(t)}{\alpha} & \text{en} & Q\,, \end{matrix} \right. \end{equation} \end{split}\]

donde \(\lambda\) es un parámetro de escala adimensional, y \(\lambda = 0\) corresponde a no aplicar un pulso DRAG y \(\dot{s}(t)\) es la derivada temporal de \(s(t)\). La elección teóricamente óptima para reducir el error de desfase es \(\lambda = 0,5\) y una elección óptima para reducir el error de fuga es \(\lambda = 1\). Intercambiar \(I\) y \(Q\) en la Ec. (3.144) corresponde al pulso DRAG para la componente \(Q\).

En la práctica, puede haber una desviación de estos dos valores óptimos, a menudo debido a distorsiones del pulso en las líneas que conducen a los qubits. Normalmente, para determinar el valor óptimo de \(\lambda\) se utilizan experimentos benchmarking aleatorios combinados con mediciones de un solo shot del estado \(\ket{2}\). Sin embargo, ampliando la implementación original del pulso DRAG, es posible reducir ambos errores simultáneamente. Introduciendo un parámetro de desfase de frecuencia \(\delta f\) en la forma de la onda (definida de forma que \(\delta f = 0\) corresponda a la frecuencia del qubit), es decir

(3.145)\[\begin{equation} s'_{\delta f} (t) = s'(t) e^{i 2 \pi \delta f t} \end{equation}\]

y eligiendo \(\lambda\) para minimizar los errores de fuga, entonces los errores de fase pueden reducirse simultáneamente. De forma similar, mediante un uso sensato de la puerta virtual \(Z\), también es posible reducir los errores de fase en combinación con el pulso DRAG para reducir las fugas. Las puertas modernas de un solo qubit que utilizan pulsos DRAG alcanzan ahora fidelidades rutinarias de \(F_{1qb} \geq 0.99\)

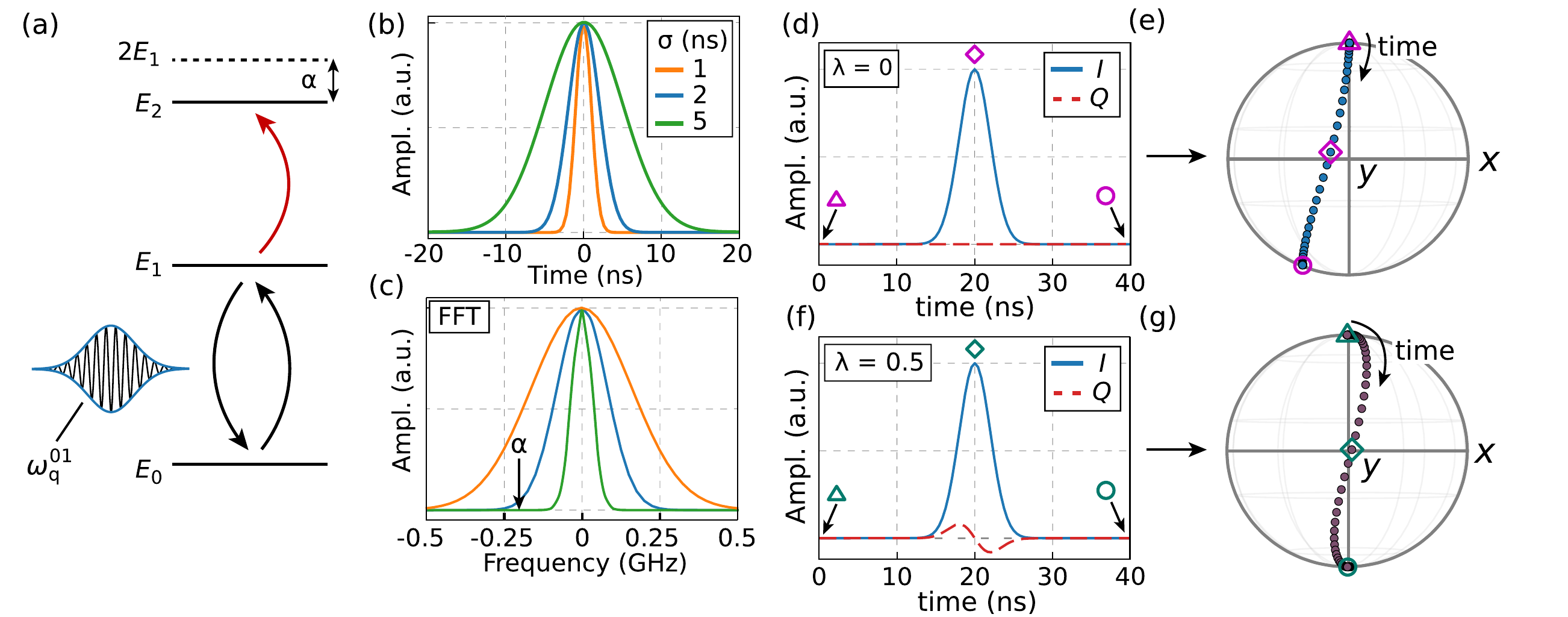
Fig. 3.20 (a) Diagrama esquemático de niveles de un qubit transmón débilmente anarmónico sometido a un pulso a la frecuencia de transición \(\omega_d = \omega_q\). (b) Forma de onda gaussiana con desviación estandar \(\sigma\). © Transformada de Fourier de (b) que muestra cómo las longitudes de pulso cortas conducen a un solapamiento significativo con la transición \(\omega_q^{1 \rightarrow 2}\), separada de \(\omega_q\) por la anarmonicidad \(\alpha\). (d) Forma de onda de un pulso \(X_\pi\) sin modulación DRAG. (e) Efecto de la forma de onda de (d) sobre un qubit inicializado en el estado \(\ket{0}\) con a \(\alpha = - 200\) MHz y \(\omega_q = 4\) GHz. El error de desfase es visible como una desviación del \(\ket{1}\) tras el pulso. (f) Forma de onda de un pulso \(X_\pi\) con modulación DRAG para un qubit con anarmonicidad \(\alpha = - 200\) MHz y parámetro DRAG \(\lambda = 0.5\) para cancelar los errores de desfase (véase el texto para más detalles). (g) Efecto de la forma de onda de (f) sobre el mismo qubit que (e). Calculado utilizando mesolve en el paquete de software QuTiP [11]. Figura tomada de [16].

---

Autor:

David Castaño (UMA-SCBI)

---

License: Licencia Creative Commons Atribución-CompartirIgual 4.0 Internacional.

This work has been financially supported by the Ministry for Digital Transformation and of Civil Service of the Spanish Government through the QUANTUM ENIA project call - Quantum Spain project, and by the European Union through the Recovery, Transformation and Resilience Plan - NextGenerationEU within the framework of the Digital Spain 2026 Agenda.