May 15, 2024 | 4 min read

Números sin complejos

\( \newcommand{\bra}[1]{\langle #1|} \) \( \newcommand{\ket}[1]{|#1\rangle} \) \( \newcommand{\braket}[2]{\langle #1|#2\rangle} \) \( \newcommand{\i}{{ i}} \) \( \newcommand{\Hil}{{\mathbb H}} \)

Show code cell source Hide code cell source

%run ../../macro_tQ.py
import sys
sys.path.append('../../')
import macro_tQ as tQ

import numpy as np

Introducción

La mecánica cuántica no se entiende sin los números complejos. Para introducirlos, empezaremos recordando que el cuadrado de un número real siempre es positivo \(a^2 >0\). Por ejemplo \(~~2^2 = 4~~\) pero también \(~~(-2)^2 = 4~~\). Por eso, decimos que la raíz cuadrada de un número sólo existe si dicho número es positivo. Es decir, \(\sqrt{4}=\pm 2\), mientras que, no sabríamos dar sentido a

\[\sqrt{-4}= \, ?\]

\(~~~\) Pregunta: \(~\) ¿cómo podríamos definir la raíz cuadrada de un número real negativo?

\(~~~\) Respuesta: \(~\) para hacerlo, es necesario ampliar el conjunto de los números reales

Definición: número \(i\)

se postula la existencia de un nuevo número, \(~i\), que es la solución única de la ecuación \(~\)

\[ i^2 = -1\]

Equivalentemente podíamos haber requerido que \(\i = \sqrt{-1}\). Ahora podemos dar sentido a la raíz cuadrada de un número negativo. Por ejemplo, \((2i)(2i) = 4 i^2 = - 4\) implica que

\[ \sqrt{-4} = 2i \]

Con el número \(i\) se opera igual que con los números reales

\[\begin{split} \begin{array}{rcl} i + i &=& 2i \\ \rule{0mm}{6mm} i - i &=& 0 \\ \rule{0mm}{6mm} i + 2i &=& 3 i \\ \rule{0mm}{6mm} i^3 &=& i*i*i = i^2 * i = -i\\ \rule{0mm}{6mm} \displaystyle \frac{i}{i} &=& 1 \rule{0mm}{6mm} \end{array} \end{split}\]

Observar que el inverso multiplicativo \(1/i\) también es \(-i\)

(1)\[\begin{eqnarray} \frac{i}{i} &=& 1 \nonumber\\ i (-i) &=& - i^2 = 1 \end{eqnarray}\]

por tanto hay una identificación importante

\[ -i = \frac{1}{i} \]

Resumen

La solución al problema planteado consiste en extender el conjunto de números reales \({\mathbb R}\) al de los complejos \({\mathbb C}\) que, ahora, incluyen el número \(i\)

Formas cartesiana y polar

Forma Cartesiana

Un número complejo, \(z \in {\mathbb C}\), se representa en forma cartesiana mediante dos números reales \(x,y\in {\mathbb R}\)

\[\begin{split} z = x + \i y ~~~~ \hbox{donde}~~~ \left\{\begin{array}{cl} x &\hbox{es la } parte~ real\\ y & \hbox{es la } parte~imaginaria \end{array} \right. \end{split}\]

Numeros complejos en python:

En python, el número imaginario \(\i\) se representa con la letra j. Añadiendo +0j convertimos un float en un complex

print(isinstance(1,complex))
print(isinstance(1+0j,complex))

False
True

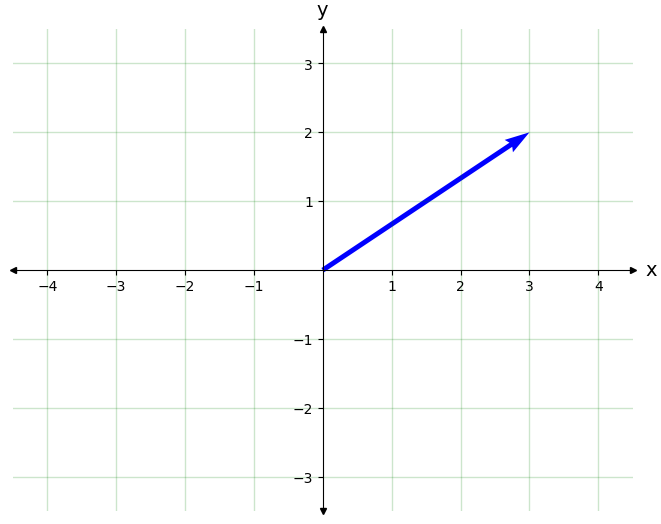
Un número complejo se puede visualizar como un vector de componentes \((x,y)\) en un plano, el plano complejo. La parte real, \(x\), es la coordenada en el eje horizontal, y la parte imaginaria, \(y\), es la coordenada en el eje vertical.

'''Forma cartesiana''' 
z = 3 + 2j

'''Extraemos las partes real e imaginaria'''
x=z.real
y=z.imag
print('z=x+iy=',x + 1j*y)

''' Representamos en el plano complejo '''
tQ.plot_complex_number(z,show_name=False,vcolor="b",sides=False,side_color="b",lwidth=1)

z=x+iy= (3+2j)

Forma Polar

Teorema: Fórmula de Euler

para todo ángulo \(\theta \in \mathbb{R}\) se cumple la siguiente identidad matemática

\[ \cos\theta + i \sin \theta = e^{i\theta} \]

La fórmula de Euler ahora nos permite representar cualquier número complejo \(z=x + \i y\) en forma polar

\[ z = \rho e^{i\theta} = \rho (\cos\theta + \i \sin\theta) \]

Los números reales \(\rho\) y \(\theta\) se denominan módulo y fase. Las componentes cartesianas son

\[x=\rho\cos\theta ~~,~~y=\rho\sin\theta\]

y por tanto \(\rho^2 = x^2 + y^2\). De la periodicidad de las funciones trigonométricas

\[ \sin\theta = \sin(\theta + 2\pi)~~~~~~~\cos\theta = \cos(\theta +2\pi) \]

se sigue que las fases \(\theta\) y \(\theta+ 2\pi n\) con \(n=0,1,2,...\) representan el mismo número complejo

\[ z = \rho e^{i\theta} = \rho e^{i(\theta + 2\pi n)} \]

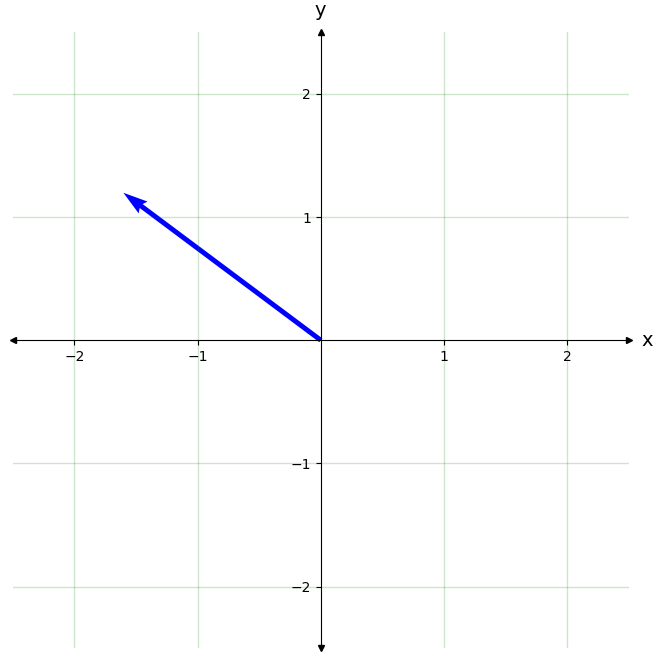
'''Forma polar'''
r=2
th=2.5
z = r*np.exp(th*1j)
print('z=',np.round(z,3))

tQ.plot_complex_number(z,show_name=False,vcolor="b",sides=False,side_color="b",lwidth=1)

z= (-1.602+1.197j)

Usar la forma polar es útil en situaciones en las que aparecen productos y potencias del número \(i\)

(2)\[\begin{eqnarray} i &=& e^{i\pi/2} \\ \rule{0mm}{8mm} -1 &=& i^2 = e^{i\pi} \\ \rule{0mm}{8mm} -i &=& i^3 = e^{3i\pi/2} =e^{-i\pi/2} \\ \end{eqnarray}\]

Ejercicio

intenta demostrar las siguientes igualdades

\[\begin{split} \begin{array}{rcl} i^i &=& e^{-\pi/2} \\ \rule{0mm}{4mm} i^{2(1+i)} &=& -e^{-\pi} \end{array} \end{split}\]

Solución

\[\begin{split} \begin{array}{rcl} i^i &=& (e^{i\pi/2})^i = e^{i^2 \pi/2} = e^{-\pi/2} \\ \rule{0mm}{6mm} i^{2(1+i)} &=& i^{2 + 2i} = i^2\, i^{2i} = i^2 \, (i^{i})^2 =(-1) (e^{-\pi/2})^2 = -e^{-\pi} \end{array} \end{split}\]

Conversión entre formas cartesiana y polar

La conversión de la representación polar a cartesiana es muy sencilla gracias a las fórmula de Euler

\[\begin{split} z = r e^{i\theta} = x + i y ~~~\hbox{ con } ~~~\left\{\begin{array}{l} x=r \cos \theta \\ \rule{0mm}{4mm} y = r\sin \theta \end{array} \right. \end{split}\]

La conversión inversa, de cartesiana a polar es un poco más delicada. Formalmente sería

\[\begin{split} z = x + i y = r e^{i\theta} ~~~ \hbox{ con } ~~~ \left\{\begin{array}{l} r=\sqrt{x^2+y^2} \\ \rule{0mm}{4mm} \theta = \arctan(y/x) \end{array} \right. \end{split}\]

A la hora de la verdad hay que fijar el signo de la función \(\arctan(y/x)\). La siguiente función examina esto mirando a los signos de \(x\) y de \(y\) para saber en qué cuadrante estamos.

'Conversión de Cartesianas a Polares'
def cartes2polar(z):

    r = np.abs(z)    
    y = z.imag
    x = z.real
    
    
    if r==0:
        print('el número 0+i0 no admite representación polar')
        th='indefinido'
    elif x==0 and y>0:  #si x=0 hay que dar la solución a mano, porque arctan(y/0) no está definido
        th=np.pi/2
    elif x==0 and y<0:
        th=3*np.pi/2  
    elif x>0 and y>=0:   #primer cuadrante
        th=np.arctan(y/x)
    elif x<0 and y>=0:   #segundo cuadrante
        th=np.arctan(-y/x)+np.pi/2
    elif x<0 and y<0:    #tercer cuadrante
        th=np.arctan(y/x)+np.pi
    elif x>0 and y<0:    #cuarto cuadrante
         th=np.arctan(-y/x)+3*np.pi/2.       
            
    return r,th

#el signo correcto también se puede conseguir usando la funcion np.arctan2(x,y)

Ejercicio

Calcula la forma polar del número complejo \(z = 4 + 3 i\) a mano y verificalo con la función que acabamos de definir

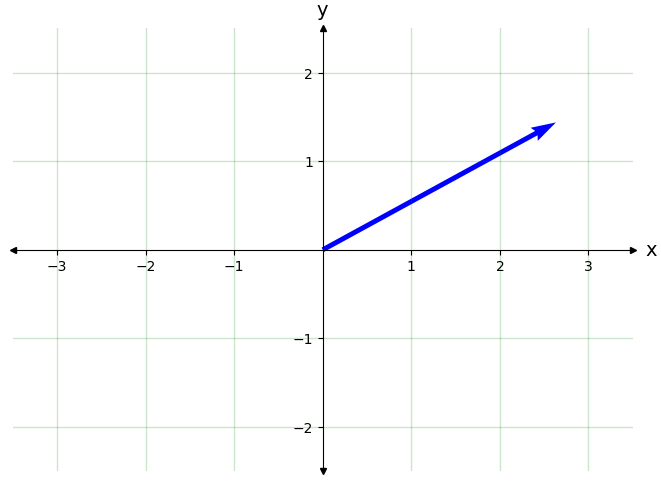
'A la inversa no es necesario definir ninguna funcion, ya que numpy directamente escribe un numero complejo en forma cartesiana'
z = 3*np.exp(1j*0.5)
print('z=',np.round(z,2))
tQ.plot_complex_number(z,show_name=False,vcolor="b",sides=False,side_color="b",lwidth=1)

z= (2.63+1.44j)

Conjugacion compleja

Todo número complejo, \(z\), lleva asociado otro, \(z^*\), denominado el complejo conjugado que se obtiene cambiando \(\i \to -\i\)

\[ z = x+\i y ~~~~\leftrightarrow~~~~ z^* = x - \i y \hspace{2cm} \]

Es evidente que \((z^*)^* = z\). Es decir, la conjugación compleja es una involución.

'''Conjugacion compleja'''
zc = np.round(z.conjugate(),2)
print('z* = ',zc)
tQ.plot_complex_number(zc,show_name=False,vcolor="r",sides=False,side_color="r",lwidth=1)

z* =  (2.63-1.44j)

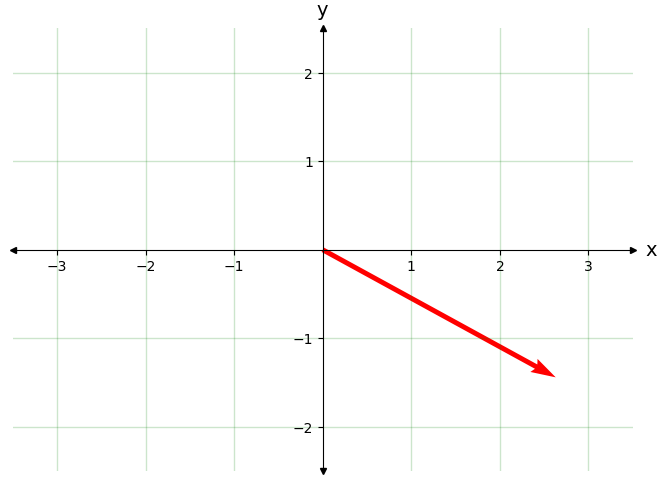
En forma polar la conjugación compleja se obtiene cambiando el signo de la fase

\[ z = \rho e^{i\theta} = \rho \cos\theta + \i \rho \sin\theta ~~\longleftrightarrow ~~ z^* = \rho e^{-i\theta} = \rho \cos\theta - \i \rho \sin\theta \hspace{4cm} \]

Operaciones básicas

Los numeros complejos \({\mathbb C}\) forman una estructura matemática, denominada cuerpo, que admiten dos operaciones internas: la suma y la multiplicación. Vamos a estudiarlas por separado

Suma

En representación cartesiana se suman las partes real e imaginaria por separado

\[ (a + \i b) + (c + \i d) = (a+c) + \i (b+d) \]

La resta es obvia, ya que \(a,b,c,d\) pueden ser números negativos.

'''Suma en cartesianas'''

z1 = 1+4j
z2 = 2+2j

'''Suma y resta'''
zs = z1+z2
zd = z1-z2

print('z1+z2=',zs)
print('z1-z2=',zd)
print('************************************')


tQ.plot_2D_plane(left=-2,right=4,up=6,down=-1) #cambiar las dimensiones para que encuadrar la figura
tQ.draw_vector(z1.real,z1.imag,'b')
tQ.draw_vector(z2.real,z2.imag,'b')
tQ.draw_vector(zs.real,zs.imag,vcolor='r')
tQ.draw_vector(zd.real,zd.imag,vcolor='g')

z1+z2= (3+6j)
z1-z2= (-1+2j)
************************************

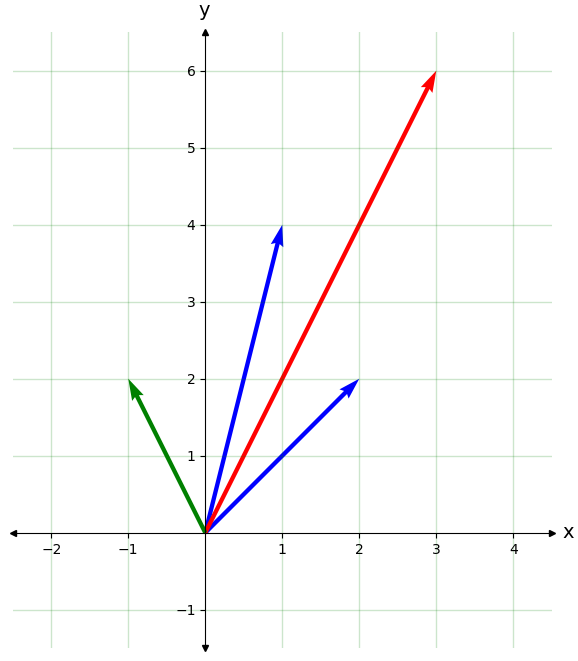
En forma polar, la suma de dos números complejos no admite ninguna simplificación, y deben transformarse primeramente a forma cartesiana, para sumarse.

\[ z + w = \rho e^{i\theta} + \sigma e^{i\phi} = (\rho\cos\theta + \sigma\cos\phi) + i(\rho\sin\theta + \sigma\sin\phi) \hspace{6cm} \]

'python directamente escribe un numero complejo en forma cartesiana'
z1 = 3*np.exp(1j*0.5)
z2 = 1*np.exp(-1j*0.7)

'''Suma y resta'''
zs = z1+z2
zd = z1-z2

print('z1+z2=',np.round(zs,4))
print('z1-z2=',np.round(zd,4))
print('************************************')

tQ.plot_2D_plane(left=-2,right=4,up=2,down=-1) #cambiar las dimensiones para que encuadrar la figura
tQ.draw_vector(z1.real,z1.imag,'b')
tQ.draw_vector(z2.real,z2.imag,'b')
tQ.draw_vector(zs.real,zs.imag,vcolor='r')
tQ.draw_vector(zd.real,zd.imag,vcolor='g')

z1+z2= (3.3976+0.7941j)
z1-z2= (1.8679+2.0825j)
************************************

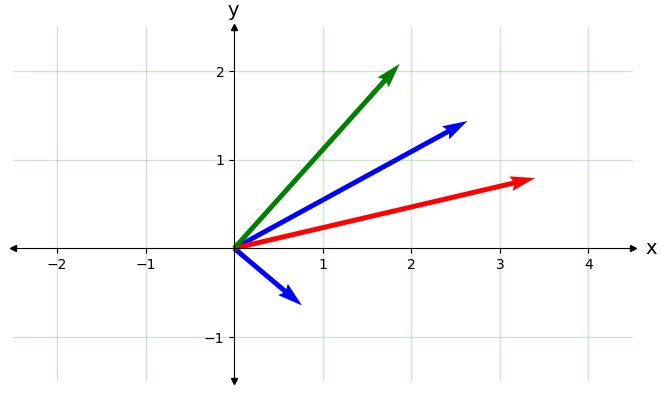
Multiplicación

En forma cartesiana la multiplicación es complicada, debiendo multiplicarse todos los factores entre sí, y teniendo en cuenta que \(\i^2= -1\)

\[ (a + \i b) (c + \i d) =ac + a\i d +\i bc +\i^2 bd = (ab - bd) + \i(ac + bd)\hspace{6cm} \]

En forma polar la multiplicación es simple: se multiplican los módulos y se suman las fases

\[ r e^{i\theta} s e^{i\phi} = rs\, e^{i(\theta + \phi)} \]

z1 = 3*np.exp(1j*0.5)
z2 = 1*np.exp(-1j*0.7)
'''Producto'''
print('z1*z2 = ', np.round(z1*z2,4))
print('z1**3 = ', np.round(pow(z1,6)))
print('************************************')

z1*z2 =  (2.9402-0.596j)
z1**3 =  (-722+103j)
************************************

Valor absoluto

El cuadrado de un número real \(a\in {\mathbb R}\) es otro número real positivo \(a^2 >0\). Ello nos permite definir el valor absoluto \(|a| = \sqrt{a^2}\) que es el mismo para \(a\) y para \(-a\).

Esto no sucede con un número complejo \(z\). Su cuadrado $\(z^2 = x^2 - y^2 +2\i xy\)$

es complejo.\(~\) Sin embargo, el producto de un número por su conjugado es un número real y positivo

\[ z z^* = (x + \i y) (x-\i y) = x^2 + ix y - i yx + y^2 = x^2 + y^2 >0 \]

Ello nos permite definir el valor absoluto de un número complejo

\[ |z| = \sqrt{z z^*} = \sqrt{x^2 + y^2} \]

Nota

el valor absoluto de un número complejo escrito en forma polar coincide con su módulo

\[ |z| = \sqrt{zz^*} = \sqrt{\rho e^{i\theta} \rho e^{-i\theta}}=\sqrt{\rho^2} = \rho \]

En consecuencia, el valor absoluto de una fase pura \(z = e^{i\theta}\) es \(\rho =1\)

División

Al igual que la multiplicación, en forma cartesiana, la división no es simple. Sea \(z = a+ \i b\) y \(w=c+\i d\)

\[ \frac{z}{w} = \frac{z}{w}\frac{w^*}{w^*} = \frac{( a+ \i b)(c-\i d)}{|w|^2} = \frac{ac+bd + \i(bc-ad)}{c^2+d^2} = \frac{ac+bd}{c^2+d^2} +\i\frac{bc-ad}{c^2+d^2} \]

En forma polar la división es tan sencilla como la multiplicación. Se toma el cociente de los módulos y la resta de las fases

\[ \frac{z}{w} = \frac{\rho e^{i\theta}}{\sigma e^{i\phi}} = \frac{\rho}{\sigma} e^{i(\theta-\phi)} \]

'''Valor absoluto'''
print('|z1|=',abs(z1))
print('comprobación |z1|=',np.sqrt(z1*z1.conjugate()).real) 
print('************************************')


'''Division'''
print('z1/z2=',np.round(z1/z2,5))
print('comprobación z1/z2=', np.round(z1*z2.conjugate()/(z2*z2.conjugate()),5))

|z1|= 3.0
comprobación |z1|= 3.0
************************************
z1/z2= (1.08707+2.79612j)
comprobación z1/z2= (1.08707+2.79612j)

Casos particulares

Vamos a ver algunas relaciones que son de uso muy frecuente.

Sumas nulas

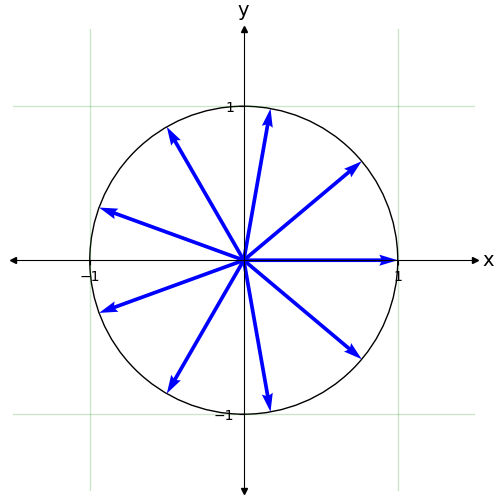
La interferencia cuántica, en ultima instancia, procede de la posibilidad de sumar muchas fases complejas de manera que se anule el resultado. Sea \(N\) un número entero cualquiera, se verifica que

\[ \sum_{k=0}^{N-1} e^{2\pi \i k/N} = e^{2\pi \i\, 0/N} + e^{2\pi \i\, 1/N} +~...~ + ~ e^{2\pi \i\, (N-1)/N} ~=~ ~0 \]

Vamos a representar los números complejos y su suma. Puedes cambiar \(N\) y también multiplicar por un módulo constante \(\rho\) y observar el resultado.

# modifica el número N
N=9
rho=1

''' Creamos las fases'''
lista_de_fases=np.exp(2*np.pi*1j*np.array(range(N))/N)
#print('lista de fases =', np.round(lista_de_fases,2))


''' Dibujamos los números complejos '''
tQ.plot_2D_plane(fsize=(6,6))
for z in rho*lista_de_fases:
    tQ.draw_vector(x=z.real,y=z.imag)

#draw_unit_circle()
plt.gca().add_patch(plt.Circle((0.,0.),1.,color='black',fill=False)) 


''' Calculamos la suma. '''
#print(lista_de_fases)
print(np.round(sum(rho*lista_de_fases),10))

(-0+0j)

Aun podemos obtener sumas nulas (interferencias) más generales. Sea \(1\leq j \leq N-1\) un número entero por el que multiplicamos todas las fases. El resultado es el mismo

\[ \sum_{k=0}^{N-1} e^{2\pi \i j k/N} = e^{2\pi \i \, 0 j/N} + e^{2\pi \i \, 1 j/N} + e^{2\pi \i \, 2 j/N} +~...~ + e^{2\pi \i\, (N-1) j/N} ~=~ ~0 \]

# cambiar el número N
N=9
rho=1
j=3
''' Creamos las fases'''
lista_de_fases=np.exp(2*j*np.pi*1j*np.array(range(N))/N)
#print('lista de fases =', np.round(lista_de_fases,2))


''' Dibujamos los números complejos '''
tQ.plot_2D_plane(fsize=(6,6))
for z in rho*lista_de_fases:
    tQ.draw_vector(x=z.real,y=z.imag)

#draw_unit_circle()
plt.gca().add_patch(plt.Circle((0.,0.),1.,color='black',fill=False)) 

''' Calculamos la suma. '''
#print(lista_de_fases)
print(np.round(sum(rho*lista_de_fases),10))

(-0+0j)

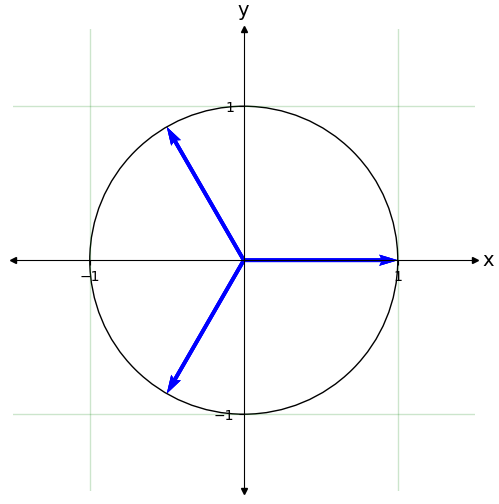
Sin embargo si \(j = 0, N, 2N,... = 0\,\hbox{mod} N\), entonces la suma no se anula y su valor es igual a \(N\).

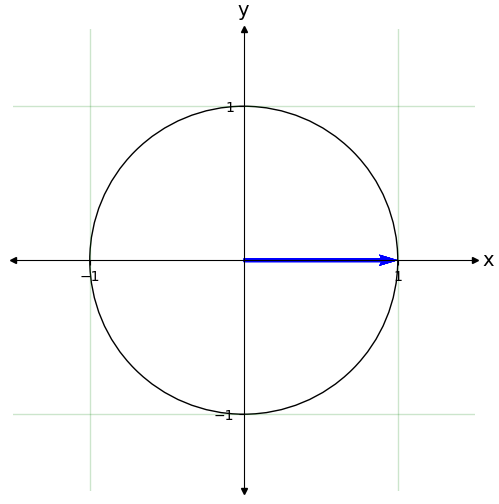
Tomemos por ejemplo \(j=N\)

\[ \sum_{k=0}^{N-1} e^{2\pi \i \, k N/N} = \sum_{k=0}^{N-1} e^{2\pi \i k} = \sum_{k=0}^{N-1} 1 =~ ~N \]

# cambiar el número N
N=9
rho=1
j=N
''' Creamos las fases'''
lista_de_fases=np.exp(2*j*np.pi*1j*np.array(range(N))/N)
#print('lista de fases =', np.round(lista_de_fases,2))


''' Dibujamos los números complejos '''
tQ.plot_2D_plane(fsize=(6,6))
for z in rho*lista_de_fases:
    tQ.draw_vector(x=z.real,y=z.imag)

#draw_unit_circle()
plt.gca().add_patch(plt.Circle((0.,0.),1.,color='black',fill=False)) 

''' Calculamos la suma. '''
#print(lista_de_fases)
print(np.round(sum(rho*lista_de_fases),10))

(9-0j)

Ejercicio

modifica la lista de fases cambiando \(j\) y \(N\) para convencerte de que todos los resultados anteriores son correctos.

Una manera de resumir todos los casos anteriores en una sola expresión involucra la función \(\delta\) de Kronecker

\[\begin{split} \delta_{ij} = \left\{ \begin{array}{rcl} 0 & \hbox{si} & i\neq 0 \\ 1 & \hbox{si} & i = j \end{array} \right. \end{split}\]

Con ella podemos enunciar el siguiente resultado general

\[ \boxed{\frac{1}{N}\sum_{k=0}^{N-1} e^{2\pi \i \, j k/N} = \delta_{j\, 0{\rm mod} N}} \]

que usaremos con frecuencia al estudiar la Transformada de Fourier Cuántica.

Desigualdad triangular

El módulo de la suma de dos números complejos verifica que

\[ | z+w| \leq |z| + |w| \]

Donde la igualdad sólo se verifica cuando ambos números complejos son paralelos en el plano complejo.

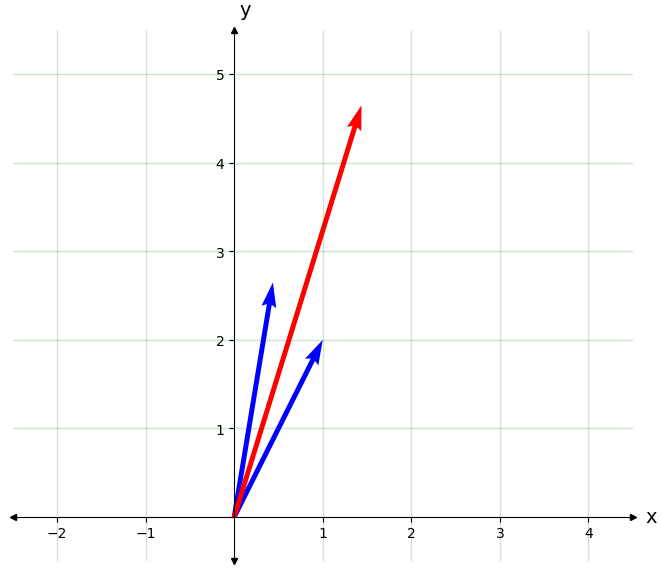
'''Comprueba que sólo cuando z1 y z2 son paralelos, se satura la desigualdad triangular'''

'''Suma en cartesianas'''
z1 = 1+2j

ang = 0.3 #el ángulo entre z1 y z2
z2 = z1*(1.2*np.exp(1j*ang))

'''Suma '''
zs = z1+z2

print('|z1|+|z2|=',abs(z1)+abs(z2))
print('|z1+z2|=',abs(z1+z2))


tQ.plot_2D_plane(left=-2,right=4,up=5,down=-0) #cambiar las dimensiones para que encuadrar la figura
tQ.draw_vector(z1.real,z1.imag,'b')
tQ.draw_vector(z2.real,z2.imag,'b')
tQ.draw_vector(zs.real,zs.imag,vcolor='r')

|z1|+|z2|= 4.919349550499537
|z1+z2|= 4.8645696489522345