May 15, 2024 | 21 min read

Operadores

\( \newcommand{\bra}[1]{\langle #1|} \) \( \newcommand{\ket}[1]{|#1\rangle} \) \( \newcommand{\braket}[2]{\langle #1|#2\rangle} \) \( \newcommand{\ketbra}[2]{| #1\rangle\mkern-1.4mu\langle #2|} \) \( \newcommand{\tr}{{\rm tr}} \) \( \newcommand{\i}{{\color{blue} i}} \) \( \newcommand{\Hil}{{\cal H}} \) \( \newcommand{\V}{{\cal V}} \) \( \newcommand{\Lin}{\hbox{Lin}} \) \( \newcommand{\boldsig}{\boldsymbol{\sigma}} \)

Show code cell source Hide code cell source

%run ../../macro_tQ.py
import sys
sys.path.append('../../')
import macro_tQ as tQ

import numpy as np
import scipy.linalg as la
from IPython.display import display,Markdown,Latex
import matplotlib.pyplot as plt
from qiskit.tools.visualization import array_to_latex
from IPython.display import display, Latex

Operador

En un espacio vectorial, además de los vectores, es necesario entender la manera en que estos se pueden transformar entre sí

Definición: Operador lineal

Un operador lineal es una aplicación \(A:\Hil \to \Hil\) que transforma un vector en otro

\[ A: \ket{u} ~~\to ~~ \ket{v} \]

de forma lineal.

La linealidad se refiere a la siguiente propiedad:

\[ A: (\alpha\ket{u} + \beta\ket{w})~~\to ~~ \ket{v} =\alpha A\ket{u} + \beta A\ket{w} \]

Ejemplo

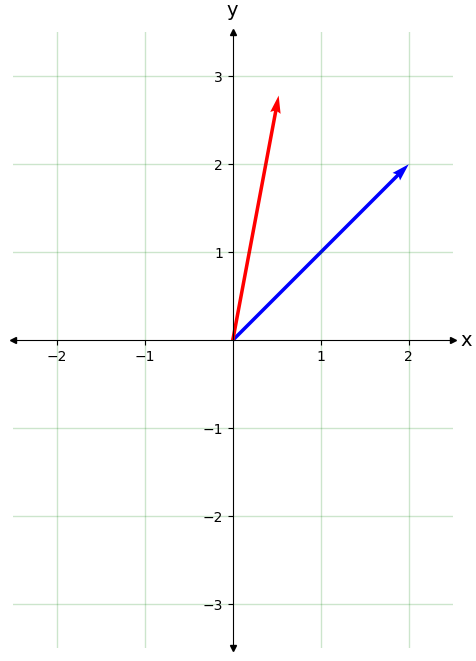
Un operador fácil de visualizar es el operador de rotación en un plano. Dado un ángulo \(\theta \in (0,2\pi)\) el operador \(A = R(\theta)\) gira cualquier vector un ángulo \(\theta\) en el sentido antihorario

Un vector en el plano \({\bf u} = (u_1,u_2)\) es equivalente al número complejo \(u = u_1 + i u_2\) en el plano complejo \(V = {\mathbb C}\).

Escrito en polares, \(u=|u|e^{i\phi}\), sabemos que una rotación de ángulo \(\theta\) es equivalente a añadirle dicho ángulo a la fase

\[ v = R(\theta) u = |u| e^{i(\phi + \theta)} = |u| e^{i\phi } e^{i\theta} = u\cdot e^{i\theta} \]

Por tanto, para rotar un número complejo un ángulo \(\theta\) basta con multiplicarlo por la fase \(e^{i\theta}\), que se corresponde con el operador \(R(\theta)\) en el espacio vectorial \(V = \mathbb{C}\). La propiedad fundamental de una rotación es la de mantener invariante el módulo \(|v| = |u|\).

'''ángulo que queremos rotar'''
theta=0.6 

'''vector a rotar'''
u1=2.
u2=2.

'Función que rota un vector tratándolo como un número complejo'
def R(u1,u2,theta):
        u = u1 + u2*1j
        v = u*np.exp(1j*theta) # u rotado un angulo theta
        return v.real,v.imag
    
'''v1 y v2 a partir de u1, u2 y theta'''
v1,v2 =  R(u1,u2,theta)

''' Representación en el plano complejo '''
v = v1**2+v2**2
tQ.plot_2D_plane(left=-int(abs(v1))-2,right=int(abs(v1))+2,up=int(abs(v2))+1,down=-int(abs(v2))-1)
tQ.draw_vector(u1,u1,vcolor='b')
tQ.draw_vector(v1,v2,vcolor='r')

Matriz de un operador

Dada una base \(\{\ket{i}\}\) con \(i=1,...,N\), podemos asociar a cada operador \(A\), una matriz \(A_{ij}\). Veamos por qué: escribamos los vectores \(\ket{u}\) y \(\ket{v} \) en la base \(\{\ket{i}\}\)

\[\begin{split} \ket{u} ~=~ \sum_{i=1}^N u_i \ket{i}~ \sim ~\begin{pmatrix} u_1 \\ v_2\\ \vdots \\ v_N\end{pmatrix} ~~~~~~~~~,~~~~~~~~ \ket{v} ~=~ \sum_{i=1}^N v_i \ket{i}~\sim ~\begin{pmatrix} v_1 \\ v_2\\ \vdots \\ v_N\end{pmatrix} \end{split}\]

El hecho de que \(\ket{v} = A\ket{u}\) donde \(A\) es un operador lineal quiere decir que existe una matriz

\[\begin{split} A ~\sim~ \begin{pmatrix} A_{11} & A_{12} & \cdots & A_{1N} \\ A_{21} & A_{22} & \cdots & A_{2N} \\ \vdots & \vdots & \ddots & \vdots \\ A_{N1} & A_{N2} & \cdots & A_{NN} \end{pmatrix} \end{split}\]

que relaciona las componentes de ambos vectores

\[\begin{split} \begin{pmatrix} v_1 \\ v_2 \\ \vdots \\ v_N \end{pmatrix} = \begin{pmatrix} A_{11} & A_{12} & \cdots & A_{1N} \\ A_{21} & A_{22} & \cdots & A_{2N} \\ \vdots & \vdots & \ddots & \vdots \\ A_{N1} & A_{N2} & \cdots & A_{NN} \end{pmatrix} \begin{pmatrix} u_1 \\ u_2 \\ \vdots \\ u_N\end{pmatrix} \end{split}\]

o, lo que es igual $\( v_i = \sum_{j=1}^N A_{ij} u_j \, \)$

Ejemplo

Continuando con el ejemplo del operador de rotación en un plano, hemos visto que las componentes de \(u = u_1 + i u_2\) y las de \(R(\theta)u = v = v_1 + i v_2\) se obtienen mediante la multiplicación por una fase pura

\[\begin{eqnarray*} v&=& u e^{i\theta} \\ \end{eqnarray*}\]

Vamos a desarrollar cada miembro en cartesianas, separando las partes real e imaginaria

\[\begin{eqnarray*} v_1 + i v_2 &=& (u_1 + iu_2) (\cos \theta + i \sin \theta) \\ \rule{0mm}{6mm} &=& (\cos\theta \, u_1 - \sin \theta\, u_2) + i(\sin\theta\, u_1 + \cos \theta\, u_2) \end{eqnarray*}\]

es decir las coordenadas del vector origen y el vector rotado imagen se relacionan en la forma

\[\begin{eqnarray*} v_1 = \cos\theta \, u_1 - \sin \theta\, u_2 ~~~~~~~,~~~~~~~~ v_2 = \sin\theta \, u_1 + \cos \theta\, u_2 \end{eqnarray*}\]

que podemos expresar en forma matricial

\[\begin{split} \begin{pmatrix} v_1 \\ v_2 \end{pmatrix} = \begin{pmatrix} \cos\theta & -\sin\theta \\ \sin\theta &\cos\theta\end{pmatrix} \begin{pmatrix} u_1 \\ u_2 \end{pmatrix} \end{split}\]

Base de Operadores

Hay una clase de operadores muy simples que se puede formar a partir de dos vectores. No son los operadores e más generales, pero servirán como base para expresar cualquier operador lineal

Producto externo

Dependiendo del orden en que los compongamos, \(~\braket{u}{v}~\) ó \(~\ketbra{v}{u}~\), el resultado es muy distinto

• El producto interno, o producto escalar es un número complejo

\[ a = \braket{u}{v} = \braket{v}{u}^* \]

• El producto externo es un operador

\[ A = \ketbra{v}{u} \]

Para comprender por qué es un operador, observamos que dicha expresión aplicada a un vector \(\ket{w}\) da otro,

\[ A : \ket{w} ~\to ~ A\ket{w} = \ket{v}\braket{u}{w}=\ket{v} \lambda = \lambda \ket{v} \]

Notar

1. El orden en que escribimos las cosas es relevante o no según los casos. Por ejemplo \(\braket{u}{v}\) y \(\ketbra{v}{u}\) son objetos radicalmente distintos: el primero es un número y el segundo es un operador. En cambio \(\ket{v} \lambda = \lambda \ket{v}\), así como \(\bra{u}\lambda = \lambda\bra{u}\), es decir, los números complejos y los \(kets\) o \(bras\) pueden escribirse en cualquier orden (decimos que conmutan).

2. La acción del operador \(A = \ket{v}\bra{u}\) es muy fácil de verbalizar:

   • el operador \(A\) toma un vector \(\ket{w}\) y lo convierte en otro paralelo a \(\ket{v}\) de módulo proporcional a \(\lambda=\braket{u}{w}\)

   • si la proyección es nula \(\lambda=0\), el operador aniquila, es decir, su imagen es el elemento neutro

La diferencia entre el producto interno \(a=\braket{u}{v}\) y el externo \(A=\ketbra{u}{v}\) tiene su reflejo en una base expresando ambos vectores, \(\ket{u} = \sum_i u_i\ket{i}\) y \(\ket{v} = \sum_j v_j \ket{j}\), en componentes en una base ortonormal

• el número complejo \(a\) es el producto escalar

\[\begin{split} a = \braket{u}{v} = \begin{pmatrix} u_1^*,...,u_N^*\end{pmatrix} \begin{pmatrix} v_1 \\ \vdots \\ v_N\end{pmatrix}\, = \sum_i u_i^*v_i \end{split}\]

• la matriz \(A_{ij}\) representa el operador \(A\) en la base \(\{\ket{i}\}\)

\[\begin{split} A = \ketbra{v}{u} ~\sim ~\begin{pmatrix} v_1 \\ \vdots \\ v_N\end{pmatrix} \begin{pmatrix} u_1^*,...,u_N^*\end{pmatrix} ~=~ \begin{pmatrix} v_1 u_1^* & v_1u_2^* & ... & v_1 u_N^* \\ v_2 u_1^* & v_2 u_1^*& ... & v_2 u_N^* \\ \vdots & \vdots & \ddots & \vdots \\ v_N u_1^* & & ... & v_N u_N^* \end{pmatrix} ~ = ~A_{ij} \end{split}\]

Base canónica de operadores

Consideremos el producto externo de dos elementos de la base ortonormal \(\ketbra{i}{j}\)

La acción sobre otro vector de la base, \(\ket{k}\), es

\[\begin{split} \ket{i}\braket{j}{k} ~=~ \left\{ \begin{array}{rl} 0 & {\rm si} ~~k\neq j \\ \ket{i} & {\rm si} ~~ k=j \end{array} \right\} ~= ~ \ket{i} \delta_{jk} \end{split}\]

La matriz asociada tiene sólo un 1 en el elemento \((ij)\) y cero en todos los demás. Por ejemplo, supongamos que \(N=4\)

\[\begin{split} \ketbra{2}{3} ~\to ~~ \begin{pmatrix} 0 \\ 1 \\ 0 \\ 0 \end{pmatrix}\begin{pmatrix} 0 & 0 & 1 & 0 \end{pmatrix} = \begin{pmatrix} 0 & 0 & 0 & 0 \\ 0 & 0 & 1& 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{pmatrix} ~~\Rightarrow ~~ A_{ij} = \delta_{i2}\delta_{j3} \end{split}\]

Teorema:

Los operadores \(\ketbra{i}{j}\) forman una base para cualquier operador lineal \(A\), donde las componentes son los elementos de matriz \(A_{ij}\)

\[ A ~=~ \sum_{i,j=1}^N A_{ij} \ketbra{i}{j} \]

>>Demostración

Verifiquemos que actúa de la forma correcta

\[\begin{split} \begin{array}{rcl} A |u\rangle &=& \sum_{i,j} A_{ij} \ketbra{i}{j} \left(\sum_k u_k |k\rangle \right) \\ &\stackrel{\rm linealidad}{=} \rule{0mm}{6mm}& \sum_{i,j} \sum_k A_{ij} | i\rangle \, u_k \langle j| k\rangle \nonumber\\ &\stackrel{\rm ortonormalidad}{=}\rule{0mm}{6mm}& \sum_{i,j,k} A_{ij} | i\rangle \, u_k \delta_{jk}\\ &=\rule{0mm}{6mm}&\sum_{ij} A_{ij}\,|i\rangle \, u_j= \sum_i \left(\sum_{j} A_{ij}\, u_j\right) |i\rangle \\ &=\rule{0mm}{6mm}&\sum_i v_i \ket{i} \nonumber\\ &=\rule{0mm}{6mm}& | v\rangle \end{array} \end{split}\]

Elementos de matriz

El producto escalar muestra ahora su utilidad de nuevo. De la misma manera que obteníamos las componentes de un vector proyectando sobre un elemento de la base

\[ v_i = \braket{i}{v} \]

ahora podemos obtener los elementos de matriz de un operador \(A\) en la forma

\[ A_{ij} = \bra{i} A \ket{j} \]

Ejercicio

comprueba la consistencia de las expresiones \(~A = \sum_{i,j=1}^N A_{ij} \ketbra{i}{j} \) y \(~A_{ij} = \bra{i} A \ket{j}\)

Resumen

Dada una base \(\{\ket{i}\}\) podemos expresar un operador mediante una matriz \(A_{ij}\). La relación concreta es

• como operador \(\to ~ A = \sum_{ij} A_{ij}\ketbra{i}{j}\)

• como elemento de matriz \(\to ~ A_{ij} = \bra{i}A\ket{j}\)

Relación de completitud

La acción del operador identidad es

\[ I\ket{v} = \ket{v} \]

En particular, sobre todo elemento de la base \(I\ket{i} = \ket{i}\). En otras palabras, el operador identidad \(I\) tiene por matriz \(I_{ij}=\delta_{ij}={\rm diagonal}\, (1,1,...,1)\) con lo que

\[ I= \sum_{ij} \delta_{ij}\ketbra{i}{j} = \sum_{i} \ketbra{i}{i} \]

Esta expresión se conoce también como relación de completitud o, también, relación de cierre y se utiliza muy frecuentemente.

Notar

La relación de completitud es, en realidad, una propiedad de cualquier base. Dicho de otro modo, si \(\{\ket{e_i}\}\) y \(\{\ket{\tilde e_i}\}\) son, ambas, bases entonces \(I\ket{e_i} = \ket{e_ i}\) y \(I\ket{\tilde e_j} = \ket{\tilde e_j}\), entonces \(+1\) es el único autovalor de \(I\) en cualquier base, y la descomposición espectral da

\[ I = \sum_{i} \ketbra{e_i}{e_i} = \sum_{j} \ketbra{\tilde e_j}{ \tilde e_j}\, . \]

Cambios de base

La relación de cierre siempre se puede insertar en cualquier momento del cálculo. Se utiliza con frecuencia para efectuar cambios de base. Efectivamente insertando la identidad delante de un elemento de la base

\[\begin{split} \begin{array}{rcl} \ket{\tilde e_j} &=& I \ket{\tilde e_j} = \sum_{i} \ket{e_i}\braket{e_i}{\tilde e_j} = \sum_i \braket{e_i}{\tilde e_j} \ket{e_i} = \sum_i U_{ij}\ket{e_i}\\ \rule{0mm}{8mm} \ket{e_j} &=& I \ket{e_j} = \sum_{i} \ket{\tilde e_j}\braket{\tilde e_j}{e_i} = \sum_i \braket{\tilde e_j}{e_i} \ket{\tilde e_j} = \sum_i U^{-1}_{ij}\ket{\tilde e_i} \end{array} \end{split}\]

donde la matrices de cambio son

\[ \boxed{ U_{ij} = \braket{e_i}{\tilde e_j}~~~~,~~~~ U^{-1}_{ij} = \braket{\tilde e_i}{e_j} } \]

Notar que la matriz inversa es igual a la adjunta

\[ U^{-1}_{ij} = \braket{\tilde e_i}{ e_j } = \braket{ e_j }{\tilde e_i}^* = (U_{ji})^* = U^\dagger_{ij} \]

Esto ocurre si y sólo si las bases \(\{\ket{e_i}\}\) y \(\{\ket{\tilde e_i}\}\) son ambas ortonormales

De la misma manera podemos relacionar las componentes de un vector en ambas bases

\[ \ket{u} = \sum_i u_i \ket{e_i} = \sum_i \tilde u_i \ket{\tilde e_i} \]

Las componentes son, en cada base

\[ u_i = \braket{e_i}{u} ~~~~~~~~~~ , ~~~~~~~~~ \tilde u_i = \braket{\tilde e_i}{u} \]

Insertando la identidad

\[ u_i = \bra{e_i}I\ket{u} = \bra{ e_i}\left( \sum_j \ket{\tilde e_j}\bra{\tilde e_j}\right) \ket{u} = \sum_j \braket{e_i}{\tilde e_j}\braket{\tilde e_j}{u} = \sum_j U_{ij} \tilde u_j \]

Es decir

\[ \tilde u_i = \sum_j U_{ij} u_j \]

Igualmente podemos hallar la regla de transformación de las matrices asociadas a un operador en dos bases distintas

\[\begin{split} \begin{array}{rcl} \tilde A_{ij} ~&=&~ \bra{\tilde e_i} A \ket{\tilde e_i} ~=~ \bra{\tilde e_i} I A I \ket{\tilde e_i}\\ \rule{0mm}{10mm} &=& \sum_{k,l=1}^N \braket{\tilde e_i}{e_k}\bra{e_k}A\ket{e_l} \braket{e_l}{\tilde e_j}\\ \rule{0mm}{8mm} &=& \sum_{k,l=1}^N U^\dagger_{ik} A_{kl} U_{lj} \end{array} \end{split}\]

Ejercicio

La matriz \(\begin{pmatrix} 0 & -i \\ i & 0\end{pmatrix}\) representa un operador \(\sigma_y\) en la base \(\{\ket{0},\ket{1}\}\). Escribe \(\sigma_y\) en la base \(\{\ket{\!+\!i}= \frac{1}{\sqrt{2}}(\ket{0}+i \ket{1}),\ket{\!-\!i}= \frac{1}{\sqrt{2}}(\ket{0}-i \ket{1})\}\)

Ejercicio

Escribe en python una función \(basis\_change\) que reciba una matriz \(U_{ij}\) de cambio de base \(\ket{\tilde e_j} = \sum_i{U_{ij}}\ket{e_i}\), la componentes \(v_i\) de un vector, ó \(A_{ij}\) de un operador, y devuelva las componentes \(\tilde v_i~\) ó \(~\tilde A_{ij}\) en la nueva base.

El Espacio Vectorial \(\Lin(\Hil)\)

El conjunto de todos los operadores lineales sobre un espacio vectorial \(\Hil\) tiene, de forma natural, una estructura de espacio vectorial que denominamos \(\Lin(\Hil)\)

Dados dos operadores, \(A\) y \(B\) tanto la suma \(C = A+B\) como la multiplicación por un número complejo \(D=\lambda A\) son nuevos operadores definidos por su acción sobre un vector cualquiera \(\ket{v}\in \Hil\)

\[ C\ket{v} ~=~ (A + B) \ket{v} = A\ket{v} + B\ket{v} \]

\[ D\ket{v} ~=~ (\lambda A) \ket{v} = \lambda (A\ket{v}) \]

Si \(\Hil\) tiene dimensión \(N\), un operador general \(A\in \Lin(\Hil)\) se especifica mediante una matriz de \(N^2\) números complejos \(\Rightarrow A = A_{ij}\ket{e_i}\bra{e_j}\). En otras palabras: la dimension (compleja) del espacio de operadores lineales es \( {\rm dim}_{\bf C}(\Lin(\Hil)) = N^2\, \)

Operador Adjunto

La conjugación adjunta se puede extender a \({\rm Lin}(\Hil)\)

\[\begin{split} \dagger ~\to ~ \left\{ \begin{matrix} z & \leftrightarrow & z^* \\ |u\rangle & \leftrightarrow & \langle u | \\ A & \leftrightarrow & A^{\dagger} \end{matrix} \right. \end{split}\]

y hay dos reglas más que permiten aplicar \(\dagger\) a sumas y productos de objetos \(a \in\{z,\ket{u},A\}\)

• linealidad \(( a + b)^\dagger = a^\dagger + b^\dagger \)

• trasposición \((ab)^\dagger = b^\dagger a^\dagger\) (sólo relevante cuando \(a\) y \(b\) no conmuten)

Por ejemplo $\( \big( A(z\ket{u})\big)^\dagger = z^*\bra{u}A^\dagger \)$

Matriz adjunta

Estas reglas nos permiten obtener el adjunto de un operador

\[ A^\dagger = \left(\sum_{ij} A_{ij}\ketbra{i}{j}\right)^\dagger = \sum_{ij}\big( A_{ij}\ketbra{i}{j}\big)^\dagger = \sum_{ij} A_{ij}^* \ketbra{j}{i}= \sum_{ji} \, A_{ji}^*\ketbra{i}{j} \]

donde en la última ecuación hemos intercambiado los nombres de los índices \(i\leftrightarrow j\). Vemos que la matriz que representa \(A^\dagger\) es la matriz adjunta de \(A_{ij}\), es decir, la traspuesta y conjugada

\[ (A^\dagger)_{ij} = A^*_{ji} = (A^{*}_{ij})^t \equiv (A_{ij})^\dagger \]

donde \(^\dagger\) significa el adjunto de un operador a la izquierda, y de una matriz a la derecha.

Traza

Definición:

La traza de un operador \(A\) se define como la suma de sus elementos de matriz diagonales en cualquier base

\[ \tr A = \sum_ i \bra{e_i} A\ket{e_i} = \sum_{i} A_{ii} \]

Para ser consistente esta definición es necesario probar que no importa la base utilizada

Lema:

La traza de un operador es independiente de la base en la que se calcule

Prueba

(4)\[\begin{eqnarray} {\rm tr} A &=&\sum_i A_{ii} =\sum_{i} \bra{i}A\ket{i} =\sum_{i} \bra{i}A\left( \sum_j\ketbra{\tilde j}{\tilde j}\right)\ket{i} \nonumber\\ &=& \sum_{ij}\bra{i}A\ket{\tilde j} \braket{\tilde j}{i} = \sum_{ij}\braket{\tilde j}{i}\bra{i}A\ket{\tilde j} \nonumber\\ &=& \sum_{j} \bra{\tilde j}\left(\sum_i\ketbra{i}{i}\right) A \ket{\tilde j}= \sum_{j} \bra{\tilde j}A\ket{\tilde j}\nonumber\\ &=& \sum_j \tilde A_{jj} \end{eqnarray}\]

La traza posee dos propiedades importantes

• linealidad :

\[ {\rm tr} (A + B ) = {\rm tr}A + {\rm tr}B \]

• ciclicidad: la traza es invariante bajo permutaciones cíclicas de los operadores en su argumento. Por ejemplo, para tres operadores \(A, B\) y \(C\)

\[ {\rm tr}(ABC)= {\rm tr}(BCA) \]

• aniquila conmutadores: para un producto de dos operadores, el anterior resultado implica que la traza de un conmutador es cero. Dicho de otra forma

\[ {\rm tr}(AB) = {\rm tr}(BA) ~~~\Rightarrow ~~~~{\rm tr}([A,B]) = 0 \, . \]

Notar

sea el operador \(A = \ketbra{u}{v}\) entonces \( \tr \left(\rule{0mm}{5mm}\ketbra{u}{v}\right) = \braket{v}{u}\). Efectivamente

\[ \tr \left(\rule{0mm}{5mm}\ketbra{u}{v}\right) = \sum_i \braket{e_i}{u}\braket{v}{e_i} = \sum_i \braket{v}{e_i} \braket{e_i}{u} = \bra{v}\left(\sum_i \ketbra{e_i}{e_i}\right) \ket{u} = \braket{v}{u} \]

Ejercicio

demuestra la ciclicidad de la traza

\(\Lin(\Hil)\) como un espacio de Hilbert

Para transformar el espacio vectorial \(\Lin(\Hil)\) en un espacio de Hilbert sólo es necesario definir un producto escalar hermítico entre dos elementos

Definición: producto escalar

dados dos operadores \(A, B \in \Lin(\Hil)\) definimos su producto escalar \(( A, B)\in {\mathbb C}\)

\[ ( A, B)\equiv {\rm tr}\left( A^\dagger B \right) \]

En una base tenemos que

\[ (A,B) = \sum_{ij} A^\dagger_{ij} B_{ji} = \sum_{ij} A^*_{ji} B_{ji} \]

mientras que

\[ (B,A) = \sum_{ij} B^\dagger_{ij} A_{ji} = \sum_{ij} B^*_{ji} A_{ji} \]

Se sigue que \((B,A) = (A,B)^*\). Además es trivial comprobar que \((A,B+C) = (A,B) + (A,C)\), por lo que se trata de un producto escalar sesquilineal o hermítico.

\(\Lin(\Hil)\) como un espacio normado

Una norma definida sobre \(\Lin(\Hil) \)es un una función real \( A\to \| A\| \in {\mathbb R}\) con las propiedades que se han definido en una sección anterior

Definición: \(p\)-norma Shatten

Dado un operador \(A\in \Lin(\Hil)\) la función

\[ \| A \|_p = \left({\rm tr} \left(A^\dagger A\right)^{p/2} \right)^{1/p} \]

define una norma, denominada \(p\)-norma de Shatten.

Los tres casos más frecuentes son

• \(p=1\) norma de la traza \(~\Rightarrow ~  \| A \|_1 = {\rm tr} \sqrt{A^\dagger A}\)

Esta norma es igual a la suma de los valores singulares de \(A ~\Rightarrow ~\| A \|_1 = \sum_i^r s_i\), donde \(s_i^2\) son los autovalores de \(A^\dagger A\)

• \(p=2\) norma de Frobenius \(~\Rightarrow ~ \| A \|_2 = \sqrt{{ \rm tr} A^\dagger A }\)

La norma de Frobenius es la que se obtiene a partir del producto escalar \(\|A\|_2 = (A,A)\)

• \(p=\infty\) norma espectral \(~\Rightarrow ~ \| A \|_\infty = \lim_{p\to \infty} \| A \|_p\)

Puede demostrarse que la norma espectral es equivalente a la siguiente definición

\[ \|A\|_\infty = \hbox{max}_{\ket{u}\in \Hil}\{ \|A\ket{u}\| ~~\hbox{con} ~ \|\ket{u}\| = 1\} \]

Ejercicio

Escribe, en python, una función \(trace\_norm(A)\), que calcule la norma de la traza de un operador.

Distancia de traza

Cualquier norma permite definir una noción de distancia o diferencia entre dos operadores.

Definición: Distancia de traza

Se define la distancia de traza entre dos operadores \(A\) y \(B\) como la norma de la diferencia

\[ d(A,B) = \| A - B \|_1 \]

Clases de operadores

Dentro de \(\Lin(\Hil)\) podemos definir subconjuntos de operadores que mantienen ciertas propiedades importantes. Algunos formarán subespacios vectoriales, y otros no. Podemos definir dichas clases de operadores pidiendo que satisfagan algúna condición o restricción.

Operador Unitario

Definición:

Un operador unitario \(U\) es tal que su adjunto es igual a su inverso

\[ U^\dagger = U^{-1} \, \]

Naturalmente, esta ecuación se traduce en la misma ecuación para las matrices asociadas en cualquier base

\[ (U_{ij})^\dagger = U_{ji}^* = U^{-1}_{ij} \]

Veamos ahora por qué hemos definido esta clase de operadores.

Teorema:

La acción de un operador unitario conserva intacto el producto escalar de dos vectores cualesquiera.

Demostración

Sea \(U\) un operador unitario, y \(\ket{\varphi'}=U\ket{\varphi}\) y \(\ket{\psi'} = U\ket{\psi}\) dos vectores transformados por \(U\), entonces

\[ \braket{\varphi'}{\psi'} = \left(\bra{\varphi}U^\dagger\right)U\ket{\psi} = \bra{\varphi} U^\dagger U \ket{\psi} = \braket{\varphi}{\psi} \]

particularizando para \(\ket{\varphi} = \ket{\psi}\) tenemos que un operador unitario conserva la norma.

\[ \|U \ket{\varphi}\| = \|\ket{\varphi}\| \]

Si conserva el producto escalar \(\Rightarrow\) entonces conserva la norma de cualquier vector \(\Rightarrow\) por tanto, conserva la distancia entre dos vectores \( d (\ket{v},\ket{w})= \| (\ket{v}-\ket{w}) \| \).

Notar

• La combinación lineal de operadores unitarios no es unitaria

\[ (a U+ bV)^\dagger = a^* V^\dagger+ b^* U^\dagger = a^* V^{-1}+ b^* U^{-1} \neq (a U+ b V)^{-1} \]

\(~\) Matemáticamente esto quiere decir que los operadores unitarios no forman un subespacio vectorial de \(\Lin(\Hil)\)

• La composición de operadores unitarios es unitaria. Si \(W = UV\) entonces

\[ W^\dagger = (UV)^\dagger = V^\dagger U^\dagger = V^{-1}U^{-1} = (UV)^{-1} = W^{-1} \]

\(~\) Matemáticamente esto quiere decir que los operadores unitarios forman un grupo: el grupo unitario \(U(N)\) si dim\((\Hil)=N\).

Bases ortonormales

• Como caso particular, aplicando un operador unitario \(U\) a una base ortonormal \(\{\ket{e_i}\}\) obtenemos otra base ortonormal \(\{\ket{\tilde e_i}\}\)

\[ \braket{\tilde e_i}{\tilde e_j} = \bra{\tilde e_i}U^\dagger U\ket{\tilde e_j} = \braket{e_i}{e_j} = \delta_{ij} \]

• Inversamente, dadas dos bases ortonormales, \(\{\ket{e_i}\}\) y \(\{\ket{\tilde e_i}\}\), el operador que las relaciona es un operador unitario

\[\begin{split} \begin{array}{rcl} U = \sum_i \ketbra{\tilde e_i}{e_i} & \Rightarrow & U\ket{e_j} = \ket{\tilde e_j} \\ \rule{0mm}{10mm} U^\dagger = \sum_i \ketbra{e_i}{\tilde e_i} & \Rightarrow & U^\dagger\ket{\tilde e_j} = \ket{e_j} ~~~\Rightarrow ~~~U^\dagger = U^{-1} \end{array} \end{split}\]

'definimos una matriz'
U=np.matrix([[1,1J],[1J, + 1]])/np.sqrt(2)
array_to_latex(U)

\[\begin{split}\begin{bmatrix} \frac{\sqrt{2}}{2} & \frac{\sqrt{2} i}{2} \\ \frac{\sqrt{2} i}{2} & \frac{\sqrt{2}}{2} \\ \end{bmatrix} \end{split}\]

'getH es un método de la clase matrix que devuelve la matriz conjugada hermítica'
Uadj=U.getH() 
array_to_latex(Uadj)

\[\begin{split}\begin{bmatrix} \frac{\sqrt{2}}{2} & - \frac{\sqrt{2} i}{2} \\ - \frac{\sqrt{2} i}{2} & \frac{\sqrt{2}}{2} \\ \end{bmatrix} \end{split}\]

'comprobamos que U es unitaria'
array_to_latex(np.dot(Uadj,U))

\[\begin{split}\begin{bmatrix} 1 & 0 \\ 0 & 1 \\ \end{bmatrix} \end{split}\]

Operador Normal

Definición:

un operador \(N\) es normal si conmuta con su adjunto

\[ NN^\dagger = N^\dagger N \]

Esta propiedad afirma que \(N\) y su adjunto, \(N^\dagger\) conmutan. La siguiente propiedad hace de los operadores normales, objetos muy importantes

Teorema:

\(N\) es un operador normal si y sólo si existe una base ortonormal, \(\{\ket{e_i}\}\), en la cual, la matriz \(N_{ij}\) que lo representa es diagonal

\[\begin{split} N_{ij} = \bra{e_i}N\ket{e_j} = \begin{bmatrix} \lambda_1 & & & \\ & \lambda_2 & & \\ & & \ddots & \\ & & & \lambda_D \end{bmatrix} \end{split}\]

Operador Hermítico

Definición:

un operador \(H\) es Hermítico (o autoadjunto) si verifica la ecuación

\[ H = H^\dagger \]

La matriz asociada a un operador hermítico también se llama hermítica, y coincide con su traspuesta y conjugada

\[ H_{ij} = H^\dagger_{ij} \equiv H^*_{ji} \]

Evidentemente, un operador hermítico conmuta con su adjunto. Por tanto es un caso particular de operador normal.

A partir de cualquier operador \(C\neq C^\dagger \) siempre podemos construir un operador hermítico \(H=H^\dagger\) mediante la combinación lineal

\[ H = C + C^\dagger \]

Esto se extiende trivialmente a las matrices que los representan en cualquier base

\[ H_{ij} = C_{ij} + C_{ji}^* \]

Notar

• La combinación lineal de operadores hermíticos con coeficientes reales es hermítica

\[ C^\dagger = (a A + b B)^\dagger = a^* A^\dagger + b^* B^\dagger = aA + b B = C \]

Matemáticamente: los operadores autoadjuntos forman un subespacio vectorial real \(\hbox{Her}(\Hil) \subset \Lin(\Hil)\).

• La composición de operadores hermíticos, en general no es hermítica

\[ (A B)^\dagger = B^\dagger A^\dagger = BA \neq AB \]

Operador semi-definido positivo

Definición:

decimos que un operador \(A\) es semi-definido positivo \(A\geq 0\) (o no-negativo) si verifica que

\[ \bra{u} A\ket{u} \geq 0 \]

para todo \(\ket{u}\in \Hil\).

Si la desigualdad es estricta \(\bra{u} A\ket{u} > 0 \, ~\forall \ket{u}\), decimos que \(A\) es un operador positivo, \(A>0\).

El siguiente teorema es el equivalente al hecho de que un número real no-negativo \(a\geq 0\) admite una raíz cuadrada real

Teorema:

un operador hermítico \(A=A^\dagger\), es semi-definido positivo \(A\geq 0\) si y sólo si existe otro operador \(B\) tal que

\[ A = B^\dagger B \]

Proyectores

El operador \(P = \ketbra{u}{u}\) proyecta cualquier vector en la dirección de \(\ket{u}\)

\[ P \ket{w} = \ket{u}\braket{u}{w} = a \ket{u} \]

donde \(a = \braket{u}{w}\) es la proyección. De la forma de \(P\) se siguen dos propiedades importantes

• es hermítico \(~\Rightarrow~ P^\dagger = (\ketbra{u}{u})^\dagger = \ketbra{u}{u} = P\)

• es idempotente \(~\Rightarrow~ P^2 = \ket{u}\braket{u}{u}\!\bra{u} = \ketbra{u}{u} = P \)

De hecho esta dos propiedades bastan para caracterizar un operador como proyector

Definición:

un proyector es un operador hermítico \(P=P^\dagger\) que verifica la ecuación

\[ P^2 = P \]

Notar

• El proyector no tiene inverso. Si existiera \(P^{-1}\), multiplicando por él la ecuación \(P^2=P\) llegaríamos a una contradicción \(P = I\).

• El proyector es un operador no-unitario: en general, la proyección reduce la norma

\[ \| P\ket{w}\|^2 = \bra{w}P^\dagger P\ket{w} = \bra{w} P\ket{w}= \braket{w}{u}\!\braket{u}{w} = |\braket{u}{w}|^2 < \|\ket{u}\|\|\ket{w}\| = 1 \]

donde hemos aplicado la desigualdad de Cauchy Schwarz estricta si suponemos que \(\ket{u}\neq\ket{w}\).

Matriz asociada a un proyector

Sea \(\{\ket{e_i}\}\) una base ortonormal. El operador \(P_1 = \ketbra{e_1}{e_1}\) proyecta cualquier vector sobre su componente a lo largo de \(\ket{e_1}\).

En forma matricial

\[\begin{split} \ketbra{e_1}{e_1} = \begin{pmatrix} 1 & 0 & ...& 0 \end{pmatrix} \begin{pmatrix} 1 \\ 0 \\ \vdots\\ 0 \end{pmatrix} = \begin{pmatrix} 1 & 0 & \cdots & 0 \\ 0 & 0 & \cdots & 0 \\ \vdots & \vdots &\vdots & \vdots \\ 0 & 0 & \cdots & 0\end{pmatrix} \end{split}\]

de modo que

\[\begin{split} \ket{e_1}\!\braket{e_1}{u} ~= ~\begin{pmatrix} 1 & 0 & \cdots & 0 \\ 0 & 0 & \cdots & 0 \\ \vdots & \vdots &\vdots & \vdots \\ 0 & 0 & \cdots & 0\end{pmatrix} \begin{pmatrix} u_1 \\ u_2 \\ \vdots \\ u_N \end{pmatrix} = \begin{pmatrix} u^1 \\ 0 \\ \vdots \\ 0 \end{pmatrix} = u^1 \ket{e_1} \end{split}\]

Si \(\ket{u} = \sum_i u^i\ket{e_i}\) es un vector unitario \(\|\ket{u}\|=1\), entonces el proyector a lo largo de \(\ket{u}\) viene dado por

\[ P(u) = \ketbra{u}{u} = \sum_{i,j} u_i u^*_j \ketbra{e_i}{e_j} \]

Es decir, le está asociada una matriz dada por \(P_{ij}=u_iu^*_j\). Es trivial verificar que

\[ P^2_{ij} = \sum_k P_{ik}P_{kj} = \sum_j u_i u^*_k u_k u^*_j = u_i\left(\sum_k u^*_k u_k\right) u_j = u_i u_j^* = P_{ij} \]

como corresponde a un proyector.

Proyector ortogonal

Sea \(P = \ketbra{u}{u}\) un proyector a lo largo de un vector \(\ket{u}.~\) Entonces el operador \( P_\perp = I - P\) verifica que

• es proyector

\[ ~~ P_\perp^2 = ( I - P)( I - P) = I - 2P + P^2 = I-P = P_\perp \]

• es perpendicular a \(P\)

\[ P_\perp P = (I - P) P = P - P^2 = P - P = 0 \]

• la identidad, \(I\) se puede descomponer como

\[I = P + P_\perp\]

Siempre podemos descomponer cualquier otro vector \(\ket{\psi}\) en sus proyecciones paralela y perpendicular a \(\ket{u}\)

\[ \ket{\psi} = ( P + P_\perp) \ket{\psi} = a \ket{u} + b \ket{u_\perp} \]

donde \(a = \braket{u}{\psi}\) y \(b = \braket{u_\perp}{\psi}\).

Los tres vectores \(\ket{\psi}, \ket{u}\) y \(\ket{u_\perp}\) están en un mismo hiperplano

d = 3
'generamos un vector aleatorio'
u = tQ.random_ket(d)
#display(array_to_latex(u))

'construimos los proyectores paralelo y perpendicular'
P_par = tQ.ket_bra(u,u);
P_perp = np.identity(d) - P_par

#display(array_to_latex(P_par))
#display(array_to_latex(P_perp))

' verificamos la propiedad  P^2 = P, y la ortogonalidad '
A = P_par@P_par - P_par
B = P_perp@P_perp - P_perp
C = P_par@P_perp

#display(array_to_latex(A))
#display(array_to_latex(B))
display(array_to_latex(C))

\[\begin{split}\begin{bmatrix} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{bmatrix} \end{split}\]

' obtener las proyecciones paralela y perpendicular de otro vector v'
v = tQ.random_ket(d)

v_par = np.dot(P_par,v)
v_perp = np.dot(P_perp,v)

' verificar perpendicularidad'
print(np.round(tQ.braket(v_par,v_perp),4))

(-0+0j)

Ejercicio (reflector)

Dado un vector unitario \(\ket{u}\), escribe

• el operador \(R_u^{\perp}\) que refleja la componente perpendicular a \(\ket{u}\) de cualquier vector \(\ket{\psi}\)

• el operador \(R_{u}^{\|}\) que refleja la componente paralela a \(\ket{u}\) de cualquier vector \(\ket{\psi}\)

Proyectores sobre un subespacio

Consideremos una base ortonormal \(\{\ket{e_i}\}~,i=1,...,N \) de \(\Hil\) y dividámosla en dos subconjuntos

\[ \{\ket{e_i}\},~ i=1,...,N_1 ~~~~~~~,~~~~~~~~\{\ket{e_{j+N_1}},~j=1,...,N_2 \]

Cualquier vector admite una descomposición ortogonal

(5)\[\begin{eqnarray} \ket{\psi} &~=~& \sum_{i=1}^N a_i \ket{e_i} ~= ~ \sum_{i=1}^N a_i \ket{e_i} + \sum_{i=1}^{N_2} a_{i+N_1} \ket{e_{i+N_1}} ~\equiv ~ \ket{\psi_1} + \ket{\psi_2}\rule{0mm}{5mm} \end{eqnarray}\]

con \(\braket{\psi_1}{\psi_2} = 0\).

Decimos que el espacio \(\Hil\) se descompone en la suma directa de subespacios ortogonales

\[ \Hil = \Hil_1 \oplus \Hil_2 \]

de dimensiones \(N_1 + N_2 = N\),

---

Los operadores

\[ P_1 = \sum_{i=1}^{N_1} \ketbra{e_i}{e_i} ~~~~~~~,~~~~~~~~ P_2 = \sum_{i=1}^{N_2} \ketbra{e_{i+N_1}}{e_{i+N_1}} = I - P_1 \]

verifican la ecuación que define un proyector \(P_1^2 = P_1,~P_2^2 = P_2\). Su acción extrae, de un vector dado, la componente sobre el subespacio asociado

\[ P_1 \ket{\psi} ~=~ \sum_{i=1}^{N_1} a_i \ket{e_i} ~=~ \ket{\psi_1} \]

\[ P_2 \ket{\psi} ~=~ \sum_{i=1}^{N_1} a_{i+N_1} \ket{e_{i+N_1}} ~=~ \ket{\psi_2} \]

Claramente verifican

\[ (P_1 + P_2)\ket{\psi} = \ket{\psi} \]

En resumen, vemos que satisfacen

\[ P_1 P_2 = P_2 P_1 = 0 ~~~,~~~~P_1 + P_2 = I \]

Notar

proyectar sobre un subespacio no es lo mismo que proyectar a lo largo de un vector. En particular \(P_1 \neq P_v = \ketbra{v}{v}\) donde \(\ket{v} =\frac{1}{\sqrt{N}} \sum_{i=1}^N \ket{e_i}\). El operador \(P_v\) proyectaría cualquier vector en la dirección de \(\ket{v}\). Por ejemplo, con \(N=2\) y \(\ket{v} = \frac{1}{\sqrt{2}}\big(\ket{e_0} + \ket{e_1}\big)\) encontramos

\[ P_v ~=~ \frac{1}{2}\big(\ket{e_0} + \ket{e_1}\big)\big(\bra{e_0} + \bra{e_1}\big)\neq \ketbra{e_0}{e_0} + \ketbra{e_1}{e_1} ~=~ P_1 \]

Autovalores y autovectores

Definición: Autovalores y autovectores

Existen vectores, \(\ket{\lambda}\) para los cuales la la acción de un operador \(A\) devuelve un vector paralelo

\[ A\ket{\lambda} = \lambda \ket{\lambda}\, \]

Decimos que \(\ket{\lambda}\) es un autovector (o vector propio) de \(A\) con autovalor (o valor propio) asociado \(\lambda\in {\mathbb C}\)

Supongamos que \(A\) tiene \(d\) vectores propios \(\ket{\lambda_j} = \sum_i v_{ij}\ket{e_i}, \, j=1,..,d\)

Sea \(U_{ij} = v_{ij}\) la matriz formada por las componentes de los vectores propios (apilados por columnas)

Entonces

\[\begin{split} A_{diag} = \begin{pmatrix} \lambda_1 & & \\ & \ddots & \\ & & \lambda_d \end{pmatrix} = U^{-1} A U \end{split}\]

Si \(A\) es normal, la matriz \(U\), que diagonaliza, es unitaria \(U^{-1} = U^{\dagger}\)

d = 2
' en general una matriz no será normal '
A = np.matrix(np.random.rand(d,d)+ np.random.rand(d,d) * 1j)
display(array_to_latex(np.dot(A,A.getH()) - np.dot(A.getH(),A)))

eigvals, eigvecs = np.linalg.eig(A)
print('valprop =',eigvals)

'verificamos que los autovectores son las columnas de v'
m=1 #cambiar a otro valor
display(array_to_latex(np.dot(A, eigvecs[:, m]) - eigvals[m] * eigvecs[:, m],prefix=r'A|\lambda_m \rangle -\lambda_m |\lambda_m\rangle =  '))

' diagonalizamos A '
U = np.matrix(eigvecs);

array_to_latex(np.dot(U.getI(),np.dot(A,U)),prefix='A_{diag} = U^{-1} A U = ')

'U no es unitaria'
array_to_latex(np.dot(U,U.getH()))

\[\begin{split}\begin{bmatrix} -0.506108732 & -0.1276862308 + 0.2099063648 i \\ -0.1276862308 - 0.2099063648 i & 0.506108732 \\ \end{bmatrix} \end{split}\]

valprop = [0.14628633+0.02682589j 0.90741489+1.07659004j]

\[\begin{split} A|\lambda_m \rangle -\lambda_m |\lambda_m\rangle = \begin{bmatrix} 0 \\ 0 \\ \end{bmatrix} \end{split}\]

\[\begin{split}\begin{bmatrix} 0.7267533292 & -0.0689374343 + 0.1133278518 i \\ -0.0689374343 - 0.1133278518 i & 1.2732466708 \\ \end{bmatrix} \end{split}\]

d = 2
'veamos ahora una matriz normal. En particular podemos tomar la parte hermítica de A'
H = 0.5*(A + A.getH())

'verificamos que es normal'
display(array_to_latex(np.dot(H,H.getH()) - np.dot(H.getH(),H)))


eigvals, eigvecs = np.linalg.eig(H)
print('valprop =',eigvals)

'verificamos que los autovectores son las columnas de v'
m=1 #cambiar a otro valor
display(array_to_latex(np.dot(H, eigvecs[:, m]) - eigvals[m] * eigvecs[:, m],prefix=r'H|\lambda_m \rangle -\lambda_m |\lambda_m\rangle =  '))

' diagonalizamos H '
U = np.matrix(eigvecs);

array_to_latex(np.dot(U.getH(),np.dot(H,U)),prefix='H_{diag} = U^{\dagger} H U = ')

'U es unitaria'
array_to_latex(np.dot(U,U.getH()))

\[\begin{split}\begin{bmatrix} 0 & 0 \\ 0 & 0 \\ \end{bmatrix} \end{split}\]

valprop = [0.09378023-1.61196687e-17j 0.95992098+1.61196687e-17j]

\[\begin{split} H|\lambda_m \rangle -\lambda_m |\lambda_m\rangle = \begin{bmatrix} 0 \\ 0 \\ \end{bmatrix} \end{split}\]

\[\begin{split}\begin{bmatrix} 1 & 0 \\ 0 & 1 \\ \end{bmatrix} \end{split}\]

Siempre que \(A\) sea diagonalizable en una base \(A\ket{\lambda_j} = \lambda_i \ket{\lambda_i}\), la traza de \(A\) será la suma de sus autovalores

\[ {\rm tr} A = \sum_i \bra{\lambda_i}A\ket{\lambda_i} = \sum_i \lambda_i \]

Subespacio Propio

Decimos que un autovalor \(\lambda_k\) es \(d_k\) veces degenerado si existen \(d_k\) autovectores linealmente independientes, \(\ket{\lambda_k^{a}}\) con \(a=1,...,d_k\) asociados al mismo autovalor

\[A\ket{\lambda_k^a} = \lambda_k \ket{\lambda_k^a}\]

Dichos autovectores generan un subespacio propio \(S(\lambda_k)\subset \Hil\). En efecto, sea \(\ket{u} = \sum_{a=1}^{d_k} c_a\ket{\lambda^a_k} \) una combinación de dichos vectores propios, entonces

(6)\[\begin{eqnarray} A \ket{u} = \sum_{a=1}^{d_k} c_a A\ket{\lambda^a_k} = \sum_{a=1}^{d_k} c_a \lambda_k\ket{\lambda^a_k} = \lambda_k \sum_{a=1}^{d_k} c_a \ket{\lambda^a_k} =\lambda_k\ket{u} \end{eqnarray}\]

Por tanto \(\ket{u}\in S(\lambda_k)\).

• El teorema de Gramm-Schmidt garantiza que podemos elegir (mediante un cambio adecuado) el conjunto \(\{\ket{\lambda_{k}^a}\}\in (\lambda_k), a=1,...,d_k\) de forma que que sea una base ortonormal $\(\braket{\lambda_{k}^a}{\lambda_{k}^b}=\delta_{ab}\)$

• El proyector sobre el subespacio propio \(S(\lambda_k)\) será $\( P_k = \sum_{a=1}^{d_k} \ketbra{\lambda_{k}^a}{\lambda_{k}^a} \)$

Ejemplo

• Llamemos \(R_z(\theta)\) el operador que efectúa una rotación en el plano \((x,y)\) de ángulo \(\theta\). Cuando \(\theta = \pi\) encontramos las siguiente acción sobre los tres elementos \(\{\hat{\bf x},\hat{\bf y},\hat{\bf z}\}\) de la base cartesiana

(7)\[\begin{eqnarray} R_z(\pi)\hat{\bf x} &=&-\hat{\bf x} \\ \rule{0mm}{6mm} R_z(\pi)\hat{\bf y} &=& -\hat{\bf y} \\ \rule{0mm}{6mm} R_z(\pi)\hat{\bf z} &=& + \hat{\bf z} \end{eqnarray}\]

• Vemos que hay un autovector \(\hat{\bf z}\) con autovalor \(+1\) y dos autovectores \(\hat{\bf x} \) y \(\hat{\bf y} \) con autovalor \(-1\).

• El espacio \({\mathbb R}^3\) se divide en dos subespacios propios de \(R_z(\pi)\), uno de dimensión 1 (a lo largo del eje \(\hat{\bf z}\)) y otro de dimensión 2 (en el plano \((\hat{\bf x},\hat{\bf y})\)).

• Los proyectores asociados serán

\[\begin{split} P_{\hat{\bf z}}= \ket{\hat{\bf z}}\bra{\hat{\bf z}}=\begin{bmatrix} 0 & & \\ & 0 & \\ & & 1 \end{bmatrix}~~~,~~~ P_{\hat{\bf x}\hat{\bf y}}= \ket{\hat{\bf x}}\bra{\hat{\bf x}}+\ket{\hat{\bf y}}\bra{\hat{\bf y}}=\begin{bmatrix} 1 & & \\ & 1 & \\ & & 0 \end{bmatrix}~~~,~~~ \end{split}\]

Espectro de Operadores: casos particulares

Espectro de Operadores Normales

Recordemos la definición de un operador normal. \(N\) será un operador normal si conmuta con su adjunto

\[ NN^\dagger = N^\dagger N \]

La importancia de los operadores normales radica en el siguiente lema

Teorema:

los autovectores de un operador normal asociados a dos autovalores distintos son ortogonales

\[ \lambda_i\neq \lambda_j~~~~\Longleftrightarrow ~~~~ \braket{\lambda_i}{\lambda_j} = 0 \]

Prueba:

De la ecuación de autovalores \(N\ket{\lambda_j} = \lambda_j \ket{\lambda_j}\), y de \(NN^\dagger = N^\dagger N\), se sigue que

\[ \bra{\lambda_j}(N^\dagger - \lambda_j^*)(N - \lambda_j) \ket{\lambda_j} = \bra{\lambda_j}(N - \lambda_j)(N^\dagger - \lambda_j^*) \ket{\lambda_j} = 0\, \]

de donde obtenemos \((N^\dagger - \lambda_j^*) \ket{\lambda_j} = 0 \Rightarrow \bra{\lambda_j} N = \bra{\lambda_j}\lambda_j\). Entonces

\[ \bra{\lambda_j}N\ket{\lambda_i} = \lambda_j \braket{\lambda_j}{\lambda_i} = \lambda_i \braket{\lambda_j}{\lambda_i} \, , \]

de donde se sigue que, para \(\lambda_i \neq \lambda_j \Rightarrow \braket{\lambda_i}{\lambda_j} = 0\).

En general, cada autovalor \(\lambda_k\) será \(d_k \geq 1\) veces degenerado. En ese caso hay \(\{\ket{\lambda^a_k}\}, a=1,...,d_k\) autovectores que generan el subespacio propio, \(S(\lambda_k)\subset \Hil \), de dimensión \(d_k\). Subespacios \(S(\lambda_k)\perp S(\lambda_j)\) son ortogonales para \(k\neq j\) según el lema.

En resumen: siempre podemos encontrar una base ortonormal de \(\Hil\), formada por autovectores de un operador normal \(N\). La relación de cierre es

\[ I = \sum_k\sum_{a=1}^{d_k} \ket{\lambda^a_k}\bra{\lambda^a_k} ~~~~~~~~~~~;~~~~~~~~~ \braket{\lambda^a_j}{\lambda^b_k} = \delta_{ab}\delta_{jk} \]

El proyector sobre el subespacio propio \(S(\lambda_k)\) será $\( P_k = \sum_{a=1}^{d_k} \ketbra{\lambda^a_k}{\lambda^a_k} \)$

Espectro de Operadores Hermíticos

El espectro de un operador hermítico \(A = A^\dagger\), tiene dos propiedades importantes:

• 1. los autovalores de un operador hermíticos son reales \(\lambda_i \in {\mathbb R}\).

• 2. los autovectores \(\ket{\lambda_i}\) de un operador hermítico asociados a autovalores distintos son ortogonales

\[ \lambda_i\neq \lambda_j ~~~\Longleftrightarrow ~~~\braket{\lambda_i}{\lambda_j} = 0\, . \]

Prueba:

1. Tomemos un autovector normalizado de \(A\), \(\ket{\lambda}\) de autovalor \(\lambda\).

\[ \lambda = \bra{\lambda}A\ket{\lambda} = (\bra{\lambda}A^\dagger\ket{\lambda})^* = (\bra{\lambda}A\ket{\lambda})^*= \lambda^* .~~~ \]

2. De hecho esta propiedad es cierta para operadores \(N\), normales. Los operadores Hermíticos son normales. De la ecuación de autovalores \(N\ket{\lambda_j} = \lambda_j \ket{\lambda_j}\), y de \(NN^\dagger = N^\dagger N\), se sigue que

\[ \bra{\lambda_j}(N^\dagger - \lambda_j^*)(N - \lambda_j) \ket{\lambda_j} = \bra{\lambda_j}(N - \lambda_j)(N^\dagger - \lambda_j^*) \ket{\lambda_j} = 0\, \]

de donde obtenemos \((N^\dagger - \lambda_j^*) \ket{\lambda_j} = 0 \Rightarrow \bra{\lambda_j} N = \bra{\lambda_j}\lambda_j\). Entonces

\[ \bra{\lambda_j}N\ket{\lambda_i} = \lambda_j \braket{\lambda_j}{\lambda_i} = \lambda_i \braket{\lambda_j}{\lambda_i} \, , \]

de donde se sigue que, para \(\lambda_i \neq \lambda_j \Rightarrow \braket{\lambda_i}{\lambda_j} = 0\). }

El conjunto de autovectores \(\ket{\lambda_i}\) de un operador hermítico forma una base ortogonal. Puede normalizarse para formar una base ortonormal

\[ \braket{\lambda_i}{\lambda_j} = \delta_{ij} \]

Ejercicio

Escribe una función, \(random\_hermitian\), que genere una matriz hermítica de dimensión \(d\).

Comprueba en distintos casos que el espectro es real.

Espectro de Operadores Unitarios

Los autovalores de un operador unitario son fases puras

\[ U^\dagger = U^{-1} ~~~\Longleftrightarrow ~~~\lambda_i = e^{i\phi_i} \]

Prueba: si \(\{\lambda_i\}\) son autovalores de \(U\), los de \(U^\dagger\) son \(\{\lambda_i^*\}\) y los de \(U^{-1}\) son \(\{\lambda_i^{-1}\}\). La única solución de la ecuación \(\lambda_i^* = \lambda_i^{-1}\) es una fase \(\lambda_i= e^{i\phi_i}\).

Espectro de Proyectores

Lema:

los autovalores de un proyector sólo pueden ser \(~0~\) ó \(~1~\)

\[ P^2= P ~~~\Longleftrightarrow ~~~\lambda_i \in \{0,1\} \]

Prueba: la ecuación

\[ P^2 = P ~~~~~\Rightarrow ~~~~~~~~ P^2 \ket{u} = P\ket{u} \]

sólo tiene dos soluciones consistentes

\[ P\ket{u} = \ket{u}~~~~~~~\hbox{y} ~~~~~~~~~~P\ket{u} = 0 \]

Espectro de Operadores que Conmutan

Cuando dos operadores conmutan entre sí, en cierto modo, se comportan como c-número. El siguiente teorema es un reflejo de esto, y tiene una importancia fundamental en la medida completa del estado de un sistema

Teorema:

Dados dos operadores \(A\) y \(B\) que conmutan, existe una base \(\{\ket{\lambda_i}\}\) de autovalores simultáneos de ambos operadores, es decir

\[ A = \lambda_i^A\ketbra{\lambda_i}{\lambda_i} ~~~~,~~~~~ B= \lambda_i^B\ketbra{\lambda_i}{\lambda_i} \]

Prueba

Supongamos que \(A\) y \(B\) conmutan. Entonces la acción de \(A\) estabiliza los subespacios propios de \(B\).

Es decir, si \(\ket{\lambda}\) es autoestado de \(B\), entonces \(B\ket{\lambda} = \ket{\mu}\) también es autoestado con idéntico autovalor. Se comprueba fácilmente

\[ A(B\ket{\lambda} ) = B(A\ket{\lambda}) = B(\lambda\ket{\lambda}) = \lambda (B\ket{\lambda}) \]

Por tanto \(\ket{\lambda}\) y \(B\ket{\lambda}\) pertenecen al mismo subespacio propio. Esto es lo que se entiende por estabilizar el subespacio.

Si \(\lambda\) es degenerado esto sólo asegura que \(B\ket{\lambda} = \ket{\lambda'}\) pertenece al subespacio propio del mismo autovalor \(\lambda\).

Esto quiere decir que, dento de cada subespacio propio de \(B\), podemos escoger la base que queramos. En particular podemos escoger una base que diagonalice \(A\) dentro de dicho subespacio.

En otras palabras, dos operadores que conmutan son diagonalizables simultáneamente. Su matriz en la base \(\{\ket{\lambda_i}\}\) es

\[\begin{split} A = \begin{bmatrix} \lambda^A_1 & & & \\ & \lambda^A_2 & & \\ & & \ddots & \\ & & & \lambda^A_n \end{bmatrix}~~~~~~~,~~~~~~~~ B = \begin{bmatrix} \lambda^B_1 & & & \\ & \lambda^B_2 & & \\ & & \ddots & \\ & & & \lambda^B_n \end{bmatrix}\, . \end{split}\]

La importancia de este teorema se manifiesta cuando \(A\) y \(B\) son observables. Supongamos que medimos \(A\) primero y obtenemos \(\lambda_1^A\). El estado obtenido será \(\ket{\lambda_1}\) el cual es, a su vez, autoestado de \(B\). Una medida de \(B\) nos dará \(\lambda_1^B\) sin ambigüedad. y no modificará el estado obtenido, que quedará preparado en un autoestado común de autovalores \((\lambda_1^A, \lambda_2^B)\).

Por tanto, la caracterización más precisa que se puede hacer de un sistema requiere la construcción de un conjunto máximal de observables que conmutan (CMOC). Su obtención es, por tanto de importancia crucial.

Valores Singulares

Un operador normal está caracterizado unívocamente por su lista de autovalores. Esto es muy útil porque podemos definir la distancia entre dos operadores a partir de la diferencia entre sus listas.

En el caso de un operador general, también podemos definir una colección de números reales que sirven como matrícula del mismo. Son los denominados valores singulares, y también nos servirá para definir la distancia entre dos operadores arbitrarios

Definición:

Se definen los valores singulares de \(A\in \Lin(\Hil)\) como \(s_i =\sqrt{\lambda_i}\) donde \(\lambda_i\) son los autovalores del operador \(A^\dagger A\).

Si \(A\in \Lin(\Hil)\) es un operador general, entonces \(A^\dagger A\) es un operador hermítico que tiene autovalores positivos o cero \(\lambda_i\geq 0\)

\[ A^\dagger A\ket{\lambda_i} = \lambda_i\ket{\lambda_i} ~~\Rightarrow ~~\lambda_i = \bra{\lambda_i} A^\dagger A\ket{\lambda_i} =\| A\ket{\lambda_i} \| \geq 0 \]

Por tanto, podemos tomar su raíz cuadrada \(s_i = \sqrt{\lambda_i} \geq 0\)

Descomposición de Operadores

Una gran cantidad de resultados relevantes sobre operadores se pueden obtener mediante una descomposición adecuada en productos o sumas de otros operadores con propiedades bien definidas. Vamos a estudiar tres tipos.

Descomposición Espectral

Teorema: descomposición espectral

Para todo operador normal \(N\) existe una base de autovectores ortonormales, \(\{\ket{\lambda^a_k}\}\), tales que
\(A\) admite la siguiente descomposición espectral

\[ N = \sum_{k=1}^d \lambda_k P_k\, . \]

Aquí \(d= {\rm dim}(\Hil)\) y \(P_k = \sum_{a=1}^{g_k} \ketbra{\lambda^a_k}{\lambda^a_k}\) es el proyector sobre el subespacio propio \(S(\lambda_k)\), donde \(\lambda_k\) es \(g_k\) veces degenerado.

La matriz \(A_{ij}\) que expresa \(A\) en la base \(\ket{\lambda_i}\) es diagonal

\[\begin{split} A_{ij} = \bra{\lambda^a_i} A\ket{\lambda^b_j} = \lambda_k \delta_{kj} \delta_{ab} =\begin{bmatrix} \lambda_1 & & & & \\ & \ddots & & & \\ & & \lambda_2 & & \\& & & \ddots & \\ & & & & \lambda_N \end{bmatrix} \end{split}\]

donde \(\lambda_k\) aparecerá \(d_k\) veces repetido.

'definamos un operador normal'
A = np.array([[1, 1], [-1, 1]])
array_to_latex(A)

' Realizamos la descomposición espectral'
eigvals, eigvecs = np.linalg.eig(A)

eigvec0 = eigvecs[:,0]
P0 = tQ.ket_bra(eigvec0,eigvec0)
display(array_to_latex(P0,prefix='P_0='))

eigvec1 = eigvecs[:,1]
P1 = tQ.ket_bra(eigvec1,eigvec1)
display(array_to_latex(P1,prefix='P_1='))

'verificamos completitud'
array_to_latex(P0+P1,prefix='P_0 + P_1=')

\[\begin{split} P_0= \begin{bmatrix} \frac{1}{2} & - \frac{i}{2} \\ \frac{i}{2} & \frac{1}{2} \\ \end{bmatrix} \end{split}\]

\[\begin{split} P_1= \begin{bmatrix} \frac{1}{2} & \frac{i}{2} \\ - \frac{i}{2} & \frac{1}{2} \\ \end{bmatrix} \end{split}\]

\[\begin{split} P_0 + P_1= \begin{bmatrix} 1 & 0 \\ 0 & 1 \\ \end{bmatrix} \end{split}\]

A_descomp_espect = eigvals[0]*P0+eigvals[1]*P1

array_to_latex(A_descomp_espect)

\[\begin{split}\begin{bmatrix} 1 & 1 \\ -1 & 1 \\ \end{bmatrix} \end{split}\]

Notar

El operador identidad tiene a cualquier vector por autovector \( I\ket{v} = \ket{v}\), con autovalores \(\lambda_ i = 1\). Por tanto, en cualquier base, la matriz asociada a \(I\) tiene la forma diagonal

\[\begin{split} I_{ij} = \delta_{ij} = \begin{pmatrix} 1 & & & \\ & 1 & & \\ & & \ddots & \\ & & & 1 \end{pmatrix} \end{split}\]

La descomposición espectral de \(I\) no es otra que la relación de completitud, que es cierta para cualquier base, ya que todas las bases son bases de autoestados de \(I\)

\[ I ~=~ \sum_{i=1}^N \ketbra{\lambda_i}{\lambda_i} ~=~ \sum_{i=1}^N \ketbra{e_i}{e_i} \]

Ejercicio

Escribe una función \(spectral\_decomp\) en python, que devuelva las dos listas \(\lambda_i\) y \(P_i\) asociadas a la decomposición espectral de un operador diagonalizable \(A = \sum_i \lambda_i P_i\).

Descomposición Polar (PD)

Teorema: descomposición polar

Todo operador \(A\in \Lin(\Hil)\) admite la descomposición polar \(A = UR\) donde \(U\) es un operador unitario, y \(R\) es un operador semi-definido positivo (sólo tiene autovalores positivos o cero)

La descomposición polar es única y generaliza la representación polar de números complejos \(z = r e^{i\phi}\) a operadores.

El hecho de que \(r\geq 0\) es la contrapartida a que \(R\) sea semi-definida positiva.

El factor \(e^{i\phi}\) es análogo al hecho de que un operador unitario, \(U\), sólo tiene autovalores que son fases puras.

Ejercicio

Escribe una función \(random\_unitary\) que genere una matriz unitaria de dimensión \(d\). Comprueba en distintos casos que el espectro está formado por fases

'''Método para construir una matriz unitaria arbitraria usando la descomposición polar'''
d = 3
A = np.matrix(np.random.rand(d,d)+ np.random.rand(d,d) * 1j)

#u, s, vh = linalg.svd(A, full_matrices=False)
u,r = la.polar(A)
    
R = np.matrix(r) 
' verificamos que R sólo tiene autovalores no-negativos '
Reigval, Reigvec = la.eig(R)
print(np.round(Reigval,3))

U=np.matrix(u) 
display(Latex('$$U = %s$$'%MatrixToLatex(U)))

''' Verifiquemos unitariedad '''
display(Latex('$$U^{\dagger}U = %s$$'%MatrixToLatex(np.dot(U.getH(),U))))

''' verificamos que los autovalores de U son fases'''
np.round([la.eig(U)[0][i]*la.eig(U)[0][i].conjugate() for i in range(d)],5)

[2.269+0.j 0.37 -0.j 0.881-0.j]

\[\begin{split}U = \begin{bmatrix} -0.09+0.18j&0.22+0.44j&0.61+0.59j \\0.69+0.32j&0.17-0.45j&-0.13+0.41j \\0.56-0.26j&0.26+0.68j&-0.25-0.18j \end{bmatrix}\end{split}\]

\[\begin{split}U^{\dagger}U = \begin{bmatrix} 1.00+0.00j&-0.00-0.00j&-0.00-0.00j \\-0.00+0.00j&1.00-0.00j&0.00-0.00j \\-0.00+0.00j&0.00+0.00j&1.00-0.00j \end{bmatrix}\end{split}\]

array([1.+0.j, 1.+0.j, 1.+0.j])

Descomposición en Valores Singulares (SVD)

Vamos a enunciar este teorema para matrices. Concretamente el teorema habla de una matriz \(m\times n\). Este tipo de matrices se corresponden con operadores \(O \in \Lin(\Hil_A,\Hil_B)\) entre espacios de dimensiones \(m\) y \(n\).

Teorema: descomposición en valores singulades SVD

Sea \(A\) una matriz compleja \(m\times n\). Entonces admite la siguiente forma representación factorizada

\[ A = U\,\Sigma\, V^{\dagger} \, , \]

donde \(U\in U(m)\), \(V\in U(n)\) son matrices unitarias cuadradas de dimensiones \(m\) y \(n\), y \(\,\Sigma \,\) es una matriz rectangular \(m\times n\) con los \(s_1, ...,s_r\) valores singulares no nulos de \(A\) en la diagonal, donde \(r\leq {\rm min}(m,n)\).

Demostración:

Prueba: Tomemos \(m>n\) sin pérdida de generalidad.

Sean \(\ket{\lambda_i}\) los \(n\) autovectores de \(A^\dagger A\in H(n)\), hermítica de dimensión \(n\).

Supongamos que hay \(r\) valores singulares \(s_i = \sqrt{\lambda_i}\) organicémolos en orden decreciente \(\lambda_1\geq \lambda_2\geq ... \geq \lambda_r > 0\) y \(\lambda_{r+1} = ... = \lambda_n = 0\).

Con la base ortonormal \(\ket{\lambda_i}\) podemos formar las siguientes matrices

\[\begin{split} \begin{array}{rcl} V(n\times n) &=& \left(\rule{0mm}{3mm} \ket{\lambda_1},\ket{\lambda_2},....,\ket{\lambda_r},\ket{\lambda_{r+1}},...,\ket{\lambda_n}\right) \nonumber \\ \Sigma(m\times n) &=& \rule{0mm}{10mm} \left( \begin{array}{ccccccc} \sqrt{\lambda_1} &\cdots & & & & & 0 \\ \vdots & \ddots & & & & & \vdots \\ & & \sqrt{\lambda_r} & & & & \\ & & & 0 & & & \\ & & & & & \ddots & \\ 0 & &\cdots & & & & 0 \\ \vdots & &&&& & \vdots \\ 0 & & \cdots & & & & 0 \end{array} \right) \nonumber \\ U(m\times m) &=& \rule{0mm}{8mm}\left( \rule{0mm}{3mm} \frac{1}{\sqrt{\lambda_1}}A\ket{\lambda_1}, \frac{1}{\sqrt{\lambda_2}}A\ket{\lambda_2}, ...., \frac{1}{\sqrt{\lambda_r}}A\ket{\lambda_r}, \ket{\mu_{r+1}},...\ket{\mu_m} \right) \, . \nonumber \end{array} \end{split}\]

donde \(\ket{\mu_{r+1}},...\ket{\mu_m}\) completa la base de vectores ortonormales. Ahora podemos operar

\[\begin{split} \begin{array}{rcl} U\Sigma V^\dagger &=& \left( \rule{0mm}{3mm} \frac{1}{\sqrt{\lambda_1}}A\ket{\lambda_1}, \frac{1}{\sqrt{\lambda_2}}A\ket{\lambda_2}, ...., \frac{1}{\sqrt{\lambda_r}}A\ket{\lambda_r}, \ket{\mu_{r+1}},...\ket{\mu_m} \right) \begin{pmatrix} \sqrt{\lambda_1}\bra{\lambda_1} \\ \sqrt{\lambda_2}\bra{\lambda_2} \\ \vdots \\ \sqrt{\lambda_r}\bra{\lambda_r} \\ 0 \\ \vdots \\ 0 \end{pmatrix} \nonumber\\ &=& A \sum_{i=1}^r \ket{\lambda_i}\bra{\lambda_i} = A \sum_{i=1}^n \ket{\lambda_i}\bra{\lambda_i} = A\, , \nonumber \end{array} \end{split}\]

donde usamos que \(A\ket{\lambda_i}=0\) para \(i>r\).

'numpy tiene la función svd para descomponer en valores singulares'

A = np.random.randn(3,2)+ 1j*np.random.randn(3,2)
display(array_to_latex(A,prefix='A='))
print( 'the shape of A is :', A.shape)


u, s, vh = la.svd(A, full_matrices=True)

print( 'the shape of u =',u.shape, ' s =', s.shape,' v =', vh.shape)

\[\begin{split} A= \begin{bmatrix} -0.7126901957 - 0.0972487589 i & 1.2558829831 - 0.4639731707 i \\ -0.0935819926 + 0.2647189485 i & 1.1015280672 + 0.3626930966 i \\ 0.9183351662 + 0.1909661953 i & -1.221830817 - 0.0795633634 i \\ \end{bmatrix} \end{split}\]

the shape of A is : (3, 2)
the shape of u = (3, 3)  s = (2,)  v = (2, 2)

U=np.matrix(u)
S=np.matrix(np.diag(s))
V=np.matrix(vh).getH()

display(array_to_latex(U,prefix='U='))
display(array_to_latex(S,prefix='S='))
display(array_to_latex(V,prefix='V='))

'''Verifiquemos unitariedad'''
display(array_to_latex(np.dot(U.getH(),U),prefix='U^{\dagger}U ='))
display(array_to_latex(np.dot(V.getH(),V),prefix='V^{\dagger}V ='))

\[\begin{split} U= \begin{bmatrix} 0.6283052802 - 0.0882838956 i & 0.0966279223 + 0.2982236005 i & 0.7037469498 - 0.0624851029 i \\ 0.4112905501 + 0.1469707118 i & -0.5258623102 - 0.658890981 i & -0.0251311342 - 0.3129530719 i \\ -0.6240531376 - 0.1312851989 i & -0.4284339927 - 0.0866114797 i & 0.6335136901 - 0.0304146014 i \\ \end{bmatrix} \end{split}\]

\[\begin{split} S= \begin{bmatrix} 2.3700209488 & 0 \\ 0 & 0.7040248748 \\ \end{bmatrix} \end{split}\]

\[\begin{split} V= \begin{bmatrix} -0.4375260683 & -0.8992057271 \\ 0.8900028769 + 0.1283192062 i & -0.4330482422 - 0.0624362102 i \\ \end{bmatrix} \end{split}\]

\[\begin{split} U^{\dagger}U = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{bmatrix} \end{split}\]

\[\begin{split} V^{\dagger}V = \begin{bmatrix} 1 & 0 \\ 0 & 1 \\ \end{bmatrix} \end{split}\]

Traza

Traza de un operador

Definición:

La traza de un operador \(A\) se define como la suma de sus elementos de matriz diagonales en cualquier base

\[ \tr A = \sum_ i \bra{e_i} A\ket{e_i} = \sum_{i} A_{ii} \]

Para ser consistente esta definición es necesario probar que no importa la base utilizada

Lema:

La traza de un operador es independiente de la base en la que se calcule

Prueba

(8)\[\begin{eqnarray} {\rm tr} A &=&\sum_i A_{ii} =\sum_{i} \bra{i}A\ket{i} =\sum_{i} \bra{i}A\left( \sum_j\ketbra{\tilde j}{\tilde j}\right)\ket{i} \nonumber\\ &=& \sum_{ij}\bra{i}A\ket{\tilde j} \braket{\tilde j}{i} = \sum_{ij}\braket{\tilde j}{i}\bra{i}A\ket{\tilde j} \nonumber\\ &=& \sum_{j} \bra{\tilde j}\left(\sum_i\ketbra{i}{i}\right) A \ket{\tilde j}= \sum_{j} \bra{\tilde j}A\ket{\tilde j}\nonumber\\ &=& \sum_j \tilde A_{jj} \end{eqnarray}\]

Por esta propiedad, siempre que \(A\) sea diagonalizable en una base \(A\ket{\lambda_j} = \lambda_i \ket{\lambda_i}\), la traza de \(A\) será la suma de sus autovalores

\[ {\rm tr} A = \sum_i \bra{\lambda_i}A\ket{\lambda_i} = \sum_i \lambda_i \]

La traza posee dos propiedades importantes

• linealidad : $\( {\rm tr} (A + B ) = {\rm tr}A + {\rm tr}B \)$

• ciclicidad: la traza es invariante bajo permutaciones cíclicas de los operadores en su argumento. Por ejemplo, para tres operadores \(A, B\) y \(C\)

\[ {\rm tr}(ABC)= {\rm tr}(BCA) \]

• aniquila conmutadores: para un producto de dos operadores, el anterior resultado implica que la traza de un conmutador es cero. Dicho de otra forma

\[ {\rm tr}(AB) = {\rm tr}(BA) ~~~\Rightarrow ~~~~{\rm tr}([A,B]) = 0 \, . \]

Notar

sea el operador \(A = \ketbra{u}{v}\) entonces \( \tr \left(\rule{0mm}{5mm}\ketbra{u}{v}\right) = \braket{v}{u}\). Efectivamente $\( \tr \left(\rule{0mm}{5mm}\ketbra{u}{v}\right) = \sum_i \braket{e_i}{u}\braket{v}{e_i} = \sum_i \braket{v}{e_i} \braket{e_i}{u} = \bra{v}\left(\sum_i \ketbra{e_i}{e_i}\right) \ket{u} = \braket{v}{u} \)$

Ejercicio

demuestra la ciclicidad de la traza

\(\Lin(\Hil)\) como un espacio de Hilbert

Para transformar \(\Lin(\Hil)\) en un espacio de Hilbert sólo es necesario definir un producto escalar hermítico

Definición: producto escalar

Dados dos operadores \(A, B \in \Lin(\Hil)\) definimos su producto escalar \(( A, B)\in {\mathbb C}\)

\[ ( A, B)= {\rm tr}\left( A^\dagger B \right) \]

En una base tenemos que

\[ (A,B) = \sum_{ij} A^\dagger_{ij} B_{ji} = \sum_{ij} A^*_{ji} B_{ji} \]

mientras que

\[ (B,A) = \sum_{ij} B^\dagger_{ij} A_{ji} = \sum_{ij} B^*_{ji} A_{ji} \]

Se sigue que \((B,A) = (A,B)^*\). Además es trivial comprobar que \((A,B+C) = (A,B) + (A,C)\), por lo que se trata de un producto escalar sesquilineal o hermítico.

\(\Lin(\Hil)\) como un espacio normado

Una norma definida sobre \(\Lin(\Hil) \)es un una función real \( A\to \| A\| \in {\mathbb R}\) con las propiedades que se han definido en una sección anterior

Definición: \(p\)-norma Shatten

Dado un operador \(A\in \Lin(\Hil)\) la función

\[ \| A \|_p = \left({\rm tr} \left(A^\dagger A\right)^{p/2} \right)^{1/p} \]

define una norma, denominada \(p\)-norma de Shatten.

Los tres casos más frecuentes son

• \(p=1\) norma de la traza \(~\Rightarrow ~  \| A \|_1 = {\rm tr} \sqrt{A^\dagger A}\)

Esta norma es igual a la suma de los valores singulares de \(A ~\Rightarrow ~\| A \|_1 = \sum_i^r s_i\), donde \(s_i^2\) son los autovalores de \(A^\dagger A\)

• \(p=2\) norma de Frobenius \(~\Rightarrow ~ \| A \|_2 = \sqrt{{ \rm tr} A^\dagger A }\)

La norma de Frobenius es la que se obtiene a partir del producto escalar \(\|A\|_2 = (A,A)\)

• \(p=\infty\) norma espectral \(~\Rightarrow ~ \| A \|_\infty = \lim_{p\to \infty} \| A \|_p\)

Puede demostrarse que la norma espectral es equivalente a la siguiente definición

\[ \|A\|_\infty = \hbox{max}_{\ket{u}\in \Hil}\{ \|A\ket{u}\| ~~\hbox{con} ~ \|\ket{u}\| = 1\} \]

Ejercicio

Escribe, en python, una función \(trace\_norm(A)\), que calcule la norma de la traza de un operador.

Distancia de traza

Cualquier norma permite definir una noción de distancia o diferencia entre dos operadores.

Definición: Distancia de traza

Se define la distancia de traza entre dos operadores \(A\) y \(B\) como la norma de la traza de la diferencia

\[ d(A,B) = \| A - B \|_1 \]

Funciones de Operadores

Funciones analíticas

Estamos acostumbrados a escribir funciones de una variable real o compleja. Por ejemplo \(f(x)= x^2\), ó, \( f(z) = e^z\).

Querríamos dar sentido a la función de un operador \( A \to f(A) \)

En el caso de que \(f(z)\) sea una función analítica expresable como una serie de Taylor en torno a \(x=0\)

\[ f(z) = \sum_{n=0}^\infty \frac{1}{n!} f^{(n)}(0)\, z^n \]

tomaremos como definición la misma serie cambiando el argumento \(x\to A\)

\[ f(A) = \sum_{n=0}^\infty \frac{1}{n!} f^{(n)}(0)\, A^n \]

Notar

• no estamos exigiendo nada a \(A\) para que definir \(f(A)\) de esta manera

• de la misma forma que, para funciones analíticas \(f(z)^* = f(z^*)\), también la definición anterior asegura que \(f(A)^\dagger = f(A^\dagger)\)

Exponencial de un operador

Un caso de uso frecuente es la exponencial de un operador

\[ \exp(A) = e^A = I + A + \frac{1}{2} A^2 + \frac{1}{3!} A^3 + ... \]

d = 2
A = 0.2*np.matrix(np.random.rand(d,d)+ np.random.rand(d,d) * 1j)

' exponencial '
array_to_latex(expm(A),prefix='e^A = ')

display(array_to_latex(expm(A),prefix='e^A = '))

' serie truncada a orden cuadrático'
Id = np.matrix(np.identity(d))
power_series = Id + A + 1./2*A*A 

display(array_to_latex(power_series,prefix= r'I + A + \frac{1}{2}A^2 = '))

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
Cell In[16], line 5
      2 A = 0.2*np.matrix(np.random.rand(d,d)+ np.random.rand(d,d) * 1j)
      4 ' exponencial '
----> 5 array_to_latex(expm(A),prefix='e^A = ')
      7 display(array_to_latex(expm(A),prefix='e^A = '))
      9 ' serie truncada a orden cuadrático'

NameError: name 'expm' is not defined

Fórmula de Baker-Campbel-Haussdorf

Una propiedad importante de la función exponencial es \(e^xe^y = e^{x+y}\). La propiedad análoga para operadores sólo es cierta cuando conmutan entre sí. Para el caso genérico tenemos dos opciones

Teorema: Baker-Campbel-Haussdorf

Sean \(A,B\subset{\rm L}(\Hil)\) dos operadores lineales genéricos. Entonces

\[ e^A e^B = e^{\left({A+B + \frac{1}{2}[A,B] + \frac{1}{12}[A,[A,B]]+ \frac{1}{12}[B,[B,A]] + ...}\right)} \]

Vemos que

• Si \(A\) y \(B\) conmutan,

\[[A,B]=0 ~\Leftrightarrow ~e^A e^B = e^{A+B}\]

• Si el conmutador de \(A\) y \(B\) es un c-número

\[[A,B]= c I ~\Leftrightarrow ~ e^A e^B = e^{A+B + \frac{c}{2}}\]

• El inverso de \(e^A\) es \(e^{-A}\). Efectivamente, como

\[[A,A]=0 \Rightarrow e^A e^{-A} = e^{A-A} = e^0 = I\]

En el caso general, \(A\) y \(B\) no conmutarán, \([A,B]\neq 0\) y se generará una serie infinita de términos. Sin embargo hay una fórmula que permite factorizar la exponencial de una suma, en forma de un productorio infinito de operadores infinitesimales \(A/n\) y \(B/n\)

Teorema: Lie-Suzuki-Trotter

Sean \(A,B\subset{\rm L}(\Hil)\) dos operadores lineales genéricos. Entonces

\[ e^{A+B} = \lim_{n\to\infty} \left(e^{{A/n}} e^{B/n}\right)^n \]

Esta expresión es la base de la simulación cuántica en circuitos cuánticos digitales

Teorema:

Sea \(A\) un operdor que verifique \(A^2 = I\), demuestra que se cumple la generalización de la ecuación de Euler

\[ e^{i \alpha\, A} = \cos \alpha \, I + i \sin \alpha \, A \]

Ejercicio

Demuestra el teorema anterior

Operadores unitarios a partir de hermíticos

Teorema:

todo operador unitario \(U\) se puede expresar como la exponencial imaginaria de un operador hermítico \(H\)

\[ U = e^{i H} \]

Efectivamente,

\[U^\dagger = \left(e^{i H}\right)^\dagger = e^{-i H^\dagger} = e^{-i H}=U^{-1}\]

por tanto, \(U\) es unitario si y sólo si \(H\) es hermítico.

Prueba

(9)\[\begin{eqnarray} U^\dagger &=& \left( e^{iH}\right)^\dagger = \left( 1+ iH + \frac{1}{2}(i H)^2 + ...\right)^\dagger \\ &=& 1 - iH^\dagger + \frac{1}{2}(-i)^2 (H^2)^\dagger + ... \\ &=& 1 - iH +\frac{1}{2} H^2 - ... \\ &=& e^{-iH}\\ \rule{0mm}{6mm} &=& U^{-1} \end{eqnarray}\]

Funciones generales

No siempre \(f(z)\) es analítica en torno a \(z=0\). Es el caso, por ejemplo, de \(f(z) = \exp(1/z)\), o de \(f(z) = \log z\). Por tanto, esta función no admite una expansión en serie de Taylor.

Aun así, si la función \(f(z)\) existe, y \(A\) es un operador normal, el operador \(f(A)\) también existe. Para construirlo es necesario recurrir a la forma diagonalizada

Teorema:

Sea \(A\) un operador diagonalizable, y sea \(A= \sum_i \lambda_i \ket{\lambda_i}\bra{\lambda_i}\) su representación espectral. Entonces el operador \(f(A)\) tiene la representación espectral siguiente

\[ f(A) = \sum_i f(\lambda_i) \ket{\lambda_i}\bra{\lambda_i} \]

En otras palabras, si la matriz \(A^{(D)}_{ij} = \lambda_i \delta_{ij} \) es diagonal, cualquier función de la misma es, trivialmente, la matriz diagonal que se obtiene evaluando \(f(\lambda_i)\)

\[\begin{split} f(A^{(D)}_{ij}) = \begin{bmatrix} f(\lambda_1)& & & \\ & f(\lambda_2) & & \\ & & \ddots & \\ & & & f(\lambda_n)\end{bmatrix} \end{split}\]

Ejemplo 1

\[e^{1/A} = \sum_i e^{1/\lambda_i} \ket{\lambda_i}\bra{\lambda_i}\]

Ejemplo 2

\[\begin{eqnarray*} {\rm tr}(A \log A) &=& {\rm tr}\left[\left(\sum_j \lambda_j \ket{\lambda_j}\bra{\lambda_j}\right)\left(\sum_k\log \lambda_k \ket{\lambda_k}\bra{\lambda_k}\right)\right] ~=~ {\rm tr}\left[\sum_k \lambda_k \log\lambda_k \ket{\lambda_k}\bra{\lambda_k} \right] \\ \rule{0mm}{20mm} &=& {\rm tr} \begin{bmatrix} \lambda_1 \log \lambda_1& & & \\ &\lambda_2 \log \lambda_2 & & \\ & & \ddots & \\ & & & \lambda_n \log \lambda_n \end{bmatrix} ~= ~ \sum_k \lambda_k \log \lambda_k \rule{0mm}{8mm} \end{eqnarray*}\]

Ahora podemos invertir la expresión que permite construir un operador unitario a partir de otro hermítico

\[ U = e^{i H} ~~~~\Leftrightarrow ~~~~ H = -i \log U \]

Matrices de Pauli

Las matrices hermíticas forman un subespacio vectorial \(\hbox{Her}(\Hil)\subset \Lin(\Hil)\) que admite una base de matrices hermíticas

Definición:

Se definen las matrices de Pauli

\[\begin{split} \sigma_x = \begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix}~~~~~,~~~~~~~~~ \sigma_y = \begin{bmatrix} 0 & -i \\ i & 0 \end{bmatrix}~~~~~,~~~~~~~~~ \sigma_z = \begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix} \, . \end{split}\]

Notar

De forma colectiva, usaremos \(\sigma_i\) donde \(\sigma_1=\sigma_x, ~ \sigma_2=\sigma_y\) y \(\sigma_3=\sigma_z\). También \(\boldsig\) denota el vector de matrices de Pauli \(\boldsig = (\sigma_1,\sigma_2,\sigma_3)\).

Si añadimos la matriz identidad \(~I = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}~ \) el conjunto \(\{I,\sigma_x,\sigma_y,\sigma_z\}\) forma una base para el espacio de matrices hermíticas \(2\times 2\)

\[\begin{eqnarray*} A = a_0 I + {\bf a} \cdot \boldsymbol{\sigma} &=& a_0 I + a_1 \sigma_1 + a_2 \sigma_2 + a_3 \sigma_3 = \begin{bmatrix} a_0 + a_3 & a_1 - i a_2 \\ a_1 + i a_2 & a_0 - a_3 \end{bmatrix} = A^\dagger \end{eqnarray*}\]

con \(a_i\in {\mathbb R}\) cuatro números reales

En total, las matrices de Pauli poseen tres propiedades que las hacen únicas

• son hermíticas \(\sigma_i^\dagger = \sigma_i\)

• son unitarias \(\sigma_i^\dagger = \sigma_i^{-1} = \sigma_i\)

• tienen traza nula \(\tr(\sigma_i) = 0\)

Composición

La composición de dos matrices de Pauli es otra matriz de Pauli que cumple la siguiente identidad

\[ \sigma_i \sigma_j = \delta_{ij}I + i\epsilon_{ijk} \sigma_k \]

donde

\[ \epsilon_{123} = \epsilon_{231}=\epsilon_{312}=1~~~~,~~~~\epsilon_{213} = \epsilon_{132}=\epsilon_{321}=-1 \]

Ejemplos:

\[\begin{eqnarray*} \sigma_1\sigma_2 &=& i \sigma_3 \\ \sigma_2\sigma_1 &=& -i \sigma_3 \\ \sigma_2\sigma_1\sigma_2 &=& \sigma_2(i\sigma_3) = i^2 \sigma_1 = -\sigma_1\\ \sigma_2\sigma_2 &=& I \end{eqnarray*}\]

s0 = np.matrix([[1,0],[0,1]])
s1 = np.matrix([[0,1],[1,0]])
s2 = np.matrix([[0,-1j],[1j,0]])
s3 = np.matrix([[1,0],[0,-1]])


'verifica todas las opciones'
print(s1*s1==s0)
print(s1*s2==1j*s3)
print(s2*s1==-1j*s3)
print(s2*s1*s2==-s1)
print(s1*s1==s0)

[[ True  True]
 [ True  True]]
[[ True  True]
 [ True  True]]
[[ True  True]
 [ True  True]]
[[ True  True]
 [ True  True]]
[[ True  True]
 [ True  True]]

Nota

De las relaciones de composición anteriores se siguen inmediatamente las siguientes reglas de (anti) conmutación

\[ \{\sigma_i,\sigma_j \} = 2\delta_{ij}~~~~~~~,~~~~~~~ ~~~[\sigma_i,\sigma_j] = 2i\epsilon_{ijk}\sigma_k \]

Las matrices de Pauli tienen traza nula $\( {\rm tr} \, \sigma_i = 0 \)$

Tomando la traza de la relación de composición obtenemos que las matrices de Pauli son ortogonales en el sentido siguiente

\[ (\sigma_i, \sigma_j) = {\rm tr}(\sigma_i\sigma_j) = {\rm tr}(\delta_{ij}I + i\epsilon_{ijk} \sigma_k) = 2\delta_{ij} \]

Exponenciación

Consideremos la matriz hermítica siguiente

\[ A = {\bf a} \cdot \boldsymbol{\sigma} \equiv a_1\sigma_1 + a_2\sigma_2 + a_3 \sigma_3 \]

con \(a_i\in {\mathbb R}\) tres números reales. Separemos \({\bf a}\) en su módulo, \(a\), y su dirección \(\hat{\bf n}\)

\[{\bf a} = (a_1,a_2,a_3) =a \left( \frac{a_1}{a},\frac{a_2}{a},\frac{a_3}{a}\right) = a\, \hat{\bf n}\]

donde \(a=|{\bf a}|=\sqrt{a_1^2+a_2^3+a_3^2}~\) y \(\hat{\bf n}\) es unitario. Entonces

\[ {\bf a} \cdot \boldsymbol{\sigma} = a\, \hat{\bf n} \cdot \boldsymbol{\sigma} \equiv a A \]

Queremos hallar la exponencial \(e^{i {\bf a} \cdot \boldsymbol{\sigma}}\).

Teorema:

\[ \exp \left( \rule{0mm}{4mm} i\, {\bf a} \cdot \boldsymbol{\sigma} \right) = (\cos a)\, I + i (\sin a)\,\hat{\bf n} \cdot \boldsymbol{\sigma} \, \]

Ejercicio

• Demuestra que \((\hat{\bf n} \cdot \boldsymbol{\sigma})^2 = I\). Esto convierte este resultado en un corolario de un teorema anteriormente demostrado.

• Demuestra el teorema a partir de la descomposición espectral de las tres matrices de Pauli, \(\sigma_x, \sigma_y \) y \(\sigma_z\).

' vamos a verificar numéricamente'
from scipy.linalg import expm

' vectors a and sigma'
avec = np.random.rand(3)
sigvec = np.array([s1,s2,s3])


'exponentiating'
adots= sum(list(avec[i]*sigvec[i] for i in range(3)))
e1 = expm(1j*adots)


'using the Euler-like formula'
a = np.linalg.norm(avec)
nvec = avec/a
ndots= sum(list(nvec[i]*sigvec[i] for i in range(3)))
e2 = np.cos(a)*s0 + 1j*np.sin(a)*(nvec[0]*sigvec[0]+nvec[1]*sigvec[1]+nvec[2]*sigvec[2])

'verify'
display(array_to_latex(e1,prefix='exp(s1)='))
display(array_to_latex(e2,prefix='exp(s1)='))

\[\begin{split} exp(s1)= \begin{bmatrix} 0.6043692766 + 0.5974933488 i & 0.4138204318 + 0.3263313132 i \\ -0.4138204318 + 0.3263313132 i & 0.6043692766 - 0.5974933488 i \\ \end{bmatrix} \end{split}\]

\[\begin{split} exp(s1)= \begin{bmatrix} 0.6043692766 + 0.5974933488 i & 0.4138204318 + 0.3263313132 i \\ -0.4138204318 + 0.3263313132 i & 0.6043692766 - 0.5974933488 i \\ \end{bmatrix} \end{split}\]