May 15, 2024 | 5 min read

Puertas cuánticas#
\( \newcommand{\bra}[1]{\langle #1|} \) \( \newcommand{\ket}[1]{|#1\rangle} \) \( \newcommand{\braket}[2]{\langle #1|#2\rangle} \) \( \newcommand{\ketbra}[2]{| #1\rangle \langle #2|} \) \( \newcommand{\tr}{{\rm tr}} \) \( \newcommand{\i}{{\color{blue} i}} \) \( \newcommand{\Hil}{{\cal H}} \) \( \newcommand{\V}{{\cal V}} \) \( \newcommand{\bn}{{\bf n}} \)
Show code cell source
%run ../../macro_tQ.py
import sys
sys.path.append('../../')
import macro_tQ as tQ
import numpy as np
from IPython.display import display,Markdown,Latex
from qiskit.visualization import array_to_latex
La propia palabra cúbit incorpora la noción de bit cuántico. Un bit es una variable binaria \(a\) que puede tomar valores enteros \( {\mathbb Z}_2= \{0, 1\}\). Un sistema físico que admita dos estados diferenciados implementa un bit. Por ejemplo: un interruptor (apagado = 0, encendido=1).
Igualmente, un sistema cuántico con dos niveles de energía diferenciados puede albergar un cúbit. Vamos a definirlo matemáticamente en este capítulo. En capítulos posteriores veremos dos implementaciones físicas: el espín de un electrón y la polarización de un fotón.
Definición:
un cúbit es un espacio de Hilbert complejo de dimensión (compleja) \(N=2\)
Esto quiere decir que el espacio de Hilbert de un cúbit es \(~\Hil \sim {\mathbb C}^2\).
Un cútrit es un espacio de Hilbert de dimensión \(N=3\), \(\Hil \sim {\mathbb C}^3\). Un cúdit de dimensión \(N=d\).
Ya hemos visto que, para trabajar en espacios vectoriales, es necesario escoger una base. La base ortonormal que usaremos se denota por \(B=\{\ket{0},\ket{1}\}\) y se denomina base computacional
Esfera de Bloch#
Si lo expresamos en la base computacional, un estado \(\ket{u} \in \Hil = \mathbb{C}^2\) será \(\ket{u} = a\ket{0} + b\ket{1}\) donde \(a\) y \(b\) son dos números complejos, es decir cuatro números reales.
Sin embargo, como cualquier estado cuántico, ha de ser un vector unitario \( \braket{u}{u} = 1\). Esto impone una ecuación \(|a|^2+|b|^2=1\), lo que nos deja tres grados de libertad reales.
Pero uno de ellos es una fase global \(\ket{u} = e^{i\phi}\ket{u}\) ¡que no tiene significado! Por lo que, realmente, necesitamos sólo dos números reales para definir el estado de un cúbit.
Lema:
El cúbit \(\ket{u}\) más general se puede representar, en la base computacional \(\{\ket{0},\ket{1}\}\), usando dos números reales (ángulos) \(\theta\in [0,\pi)\) y \(\varphi\in [0,2\pi)\)
Demostración
Para demostrar el lema escribimos un vector de estado general usando la representación polar para las componentes complejas
donde hemos hecho uso de la irrelevancia de una fase global para descartar \(e^{i b_0}\) en la última línea.
Ahora \(a_1\) y \(a_0\) no son números independientes sino que verifican \(a_0^2 + a_1^2 = 0\) para que \(\|\ket{u}\|=1\). Esta ecuación se puede resolver en términos de un ángulo \(\theta/2\) tal que $\( a_0 = \cos\frac{\theta}{2}~~~,~~~ a_1 = \sin\frac{\theta}{2} \)\( Por su parte, de los números \)b_1, b_2\( sólo la diferencia \)\( \varphi = b_1-b_2 \)\( es relevante para especificar \)\ket{u} ~~~\rule{3mm}{3mm}$
En componentes en la base \(Z\) escribimos equivalentemente
El rango de \(\theta\in [0,\pi)\) y \(\varphi\in [0,2\pi)\) permite interpretar estos números reales como ángulos sobre la esfera unidad. Dicho de otro modo, podemos representar cada estado de un cúbit como un punto sobre una esfera de radio unidad: la esfera de Bloch.
\(\theta\in [0,\pi)\) el ángulo azimutal se mide desde el eje \(Z\). De modo que \(\theta=\pi/2\) es el ecuador de la esfera de Bloch.
\(\phi\in [0,2\pi)\) el ángulo polar en torno al eje \(Z\), medido a partir del plano \(XZ\)

Vectores en la Esfera de Bloch: visualizaciones#
La clase statevector en qiskit cuenta con varios visualizadores.
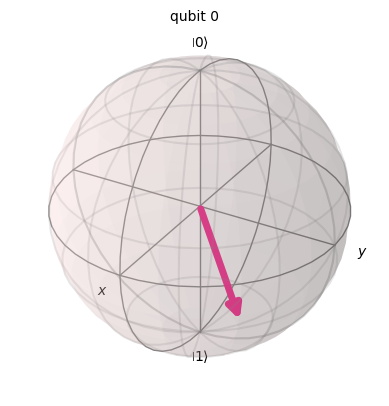
Esta rutina introduce dos ángulos \(\theta\in(0,\pi)\) y \(\phi\in(0,2\pi)\) y devuelve el vector de Bloch
theta = 1.9
phi = 0.8
psi_ket = np.array([np.cos(theta/2),(np.exp(1j*phi))*np.sin(theta/2)]).reshape(2,1)
array_to_latex(psi_ket,prefix= '\ket{\psi} = ')
from qiskit.quantum_info import Statevector
from qiskit.visualization import plot_bloch_multivector, array_to_latex
display(Statevector(psi_ket).draw('latex',prefix='\ket{\psi} = '))
Statevector(psi_ket).draw('Bloch')
Bases#
Dos vectores diametralmente opuestos en la esfera de Bloch forman una base ortonormal del espacio de un cúbit. Los denotamos \(\{\ket{0}_{\bf n},\ket{1}_{\bf n}\}\).

Base Z
\((\theta,\phi) = (0,0) \Rightarrow \ket{0}_Z = \ket{0}\)
\((\theta,\phi) = (\pi,\phi) \Rightarrow e^{i\phi}\ket{1}_Z = \ket{1}\)

Base X
\((\theta,\phi) = (\pi/2,0) ~\Rightarrow~ \frac{1}{\sqrt{2}}\big(|0\rangle+|1\rangle \big) =\ket{0}_X \equiv |+\rangle\)
\((\theta,\phi) = (\pi/2,\pi) ~\Rightarrow~ \frac{1}{\sqrt{2}}\big(|0\rangle-|1\rangle \big)=\ket{1}_X \equiv |-\rangle\)

Base Y
\((\theta,\phi) = (\pi/2,\pi/2) ~\Rightarrow ~|u\rangle =\frac{1}{\sqrt{2}}\big(|0\rangle+i|1\rangle\big) =\ket{0}_Y \equiv |+i\rangle\)
\((\theta,\phi) = (\pi/2,3\pi/2) ~\Rightarrow ~|u\rangle = \frac{1}{\sqrt{2}}\big(|0\rangle-i|1\rangle\big) = \ket{1}_Y \equiv |-i\rangle\)

Rotaciones en la esfera de Bloch#
Un operador unitario conserva la norma y, por tanto, lleva un vector a otro de la misma esfera de Bloch
Esta operación se puede visualizar como una rotación de un cierto ángulo en torno a algún eje.

Teorema:
El operador que efectúa una rotación de ángulo \(\alpha\in [0,2\pi)\) en torno al eje que marca un vector unitario \(\hat{\bf n}\) es el siguiente
donde \(\boldsymbol{\sigma} = (\sigma_x, \sigma_y, \sigma_z)\) son las matrices de Pauli
Nota
El sentido de la rotación que produce \(R_{\hat{\bf n}}(\alpha)\) en torno al eje \(\hat{\bf n}\), viene dado por la regla de la mano derecha o, también, anti-horario.
Haciendo la suma explícitamente podemos escribir la matriz unitaria
Rotaciones X, Y y Z#
Asociado a rotaciones en torno a los ejes \(X\), \(Y\) y \(Z\) de un ángulo \(\alpha\) encontramos las tres puertas siguientes
Parametrización de Euler#
Necesitamos 3 parámetros para especificar una rotación general. En \(R_{\hat{\bf n}}(\theta)\) un parámetro es \(\theta\) y otros dos entran en \(\hat{\bf n}\) con \( |\hat{\bf n}|=1\).
La parametrización de Euler consiste en una composición de tres rotaciones sucesivas en torno a los ejes \(z\), después \(y\) y finalmente \(z\) de nuevo:
Multiplicando las matrices asociadas, y extrayendo una fase global, definimos el operador \(U (\theta,\phi,\varphi)\) mediante
Los ángulos de Euler son \(\theta,\phi \) y \(\varphi\),
Rotación general#
Operando se llega a la siguiente expresión
Es evidente que la acción de este operador sobre la base \(\{\ket{0},\ket{1}\}\) una base alineada con el eje \((\theta,\phi)\)
Puertas Simples#
Por puertas simples entendemos un conjunto de operadores unitarios que se utilizan con frecuencia en la computación cuántica. Vamos a ver las puertas simples sobre 1 cúbit
Puerta de fase#
\(P_\alpha = P(\alpha)\) con \(\alpha \in [0,2\pi)\)
es unitaria para todo \(\alpha\) como se comprueba fácilmente. Aplicada a un estado de cúbit genérico
El efecto de este operador es rotar cualquier cúbit en torno al eje Z un ángulo \(\alpha\). Comprobamos que está relacionada con \(R_z(\alpha)\)
La fase global es trivial. Por tanto los dos operadores \(P(\alpha)\) y \(R_Z(\alpha)\) son equivalentes y producen el mismo efecto sobre la esfera de Bloch.
\(K_\alpha = K(\alpha)\)
realmente es una fase trivial, pero a veces se utiliza
Puertas Discretas#
Hay una serie de rotaciones discretas que forman un conjunto de puertas elementales de gran utilidad
\(X,Y,Z\)
\(S,T\)
Cualquier potencia de un operador unitario \(U\) es otro operador unitario \(U^\alpha\). Así obtenemos
\(H\)
La puerta de Hadamard, \(H\), es la primera puerta genuinamente cuántica en el sentido de que lleva un estado de la base a una superposición coherente
Podemos escribir este operador en la base canónica \(H = H_{ij}\ketbra{i}{j}\)
De aquí obtenemos la representación matricial
Nota
en cálculos posteriores encontraremos muy útil la siguiente representación de la acción de \(H\)
Como cualquier puerta, la acción de \(H\) puede visualizarse como una rotación en la esfera de Bloch \(H\) de \(\pi\) radianes en torno a un eje diagonal situado a 45\(^\circ\) entre el eje \(x\) y el eje \(y\). Esta rotación permuta los ejes \(x\) y \(z\) y cambia de sentido el eje \(y\).
La composición de dos operadores \(H\) es la identidad
o, lo qué es igual \(H = H^{-1}\). Las puertas \(X,Y,Z\) y \(H\) son unitarias y a la vez hermíticas.
Circuitos Cuánticos#
Un circuito cuántico representa la acción de un operador sobre un estado inicial \(\ket{0}\). Es decir
se representa graficamente en la forma

Cuando el operador \(U\) es una composición de puertas, por ejemplo que \(U = TH\), el orden en el que aparecen en el circuito es el inverso

#from qibo import Circuit, gates
from qibo.models.circuit import Circuit,gates
qc = Circuit(1)
qc.add(gates.H(0))
qc.add(gates.T(0))
#print(qc.draw())
tQ.draw_qibo_circuit_mpl(qc)
from qiskit import QuantumRegister, QuantumCircuit
from qiskit.quantum_info import Statevector
qr = QuantumRegister(1) #define el registo cuántico
qc = QuantumCircuit(qr) #crea un circuito
'añade puertas'
qc.h(0)
qc.t(0)
# qc.u(theta,phi,lambda,quantum register) https://qiskit.org/documentation/stubs/qiskit.circuit.library.UGate.html
#qc.u(np.pi/4,np.pi/2,0,0)
display(qc.draw(output='mpl'))
#Statevector(qc).draw('Bloch')
/opt/anaconda3/envs/TalentQ/lib/python3.11/site-packages/qiskit/visualization/circuit/matplotlib.py:266: FutureWarning: The default matplotlib drawer scheme will be changed to "iqp" in a following release. To silence this warning, specify the current default explicitly as style="clifford", or the new default as style="iqp".
self._style, def_font_ratio = load_style(self._style)
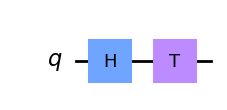
La concatenación de puertas se corresponde con la composición de operadores, es decir, con la multiplicación de las matrices asociadas.
Matriz de un circuito#
Εl circuito anterior representa el operador unitario \(U\) al que le corresponde la matriz obtenida por multiplicación
Podemos extraer el operador asociado a un circuito.
from qiskit.quantum_info import Operator
result = Operator(qc).data
from qiskit.visualization import array_to_latex
array_to_latex(result,prefix='U = ')
---------------------------------------------------------------------------
QiskitError Traceback (most recent call last)
Cell In[5], line 2
1 from qiskit.quantum_info import Operator
----> 2 result = Operator(qc).data
4 from qiskit.visualization import array_to_latex
5 array_to_latex(result,prefix='U = ')
File /opt/anaconda3/envs/TalentQ/lib/python3.11/site-packages/qiskit/quantum_info/operators/operator.py:111, in Operator.__init__(self, data, input_dims, output_dims)
109 self._data = np.asarray(data.to_matrix(), dtype=complex)
110 else:
--> 111 raise QiskitError("Invalid input data format for Operator")
113 super().__init__(
114 op_shape=op_shape,
115 input_dims=input_dims,
116 output_dims=output_dims,
117 shape=self._data.shape,
118 )
QiskitError: 'Invalid input data format for Operator'
Simulador de estado#
La descomposición en puertas nos permite visualizar la acción del operador sobre el estado de referencia \(\ket{0}\)
el operador \(H\) lleva el vector \(\ket{0}\) al vector \(\ket{+}\) sobre el eje \(x\).
posterioremente, \(T\) es una rotación de ángulo \(\pi/4\) en torno al eje \(z\).
El resultado será un vector en el plano ecuatorial en la diagonal entre los ejes \(x\) e \(y\). Podemos visualizar esto usando un simulador de vector de estado.
from qiskit.quantum_info import Statevector
statevector = Statevector(qc)
display(statevector.draw('latex',prefix='\ket{\psi} = '))
# alternative wat to plot the state vector on the Bloch sphere
statevector.draw('Bloch')
---------------------------------------------------------------------------
QiskitError Traceback (most recent call last)
Cell In[6], line 2
1 from qiskit.quantum_info import Statevector
----> 2 statevector = Statevector(qc)
4 display(statevector.draw('latex',prefix='\ket{\psi} = '))
6 # alternative wat to plot the state vector on the Bloch sphere
File /opt/anaconda3/envs/TalentQ/lib/python3.11/site-packages/qiskit/quantum_info/states/statevector.py:93, in Statevector.__init__(self, data, dims)
91 self._data = Statevector.from_instruction(data).data
92 else:
---> 93 raise QiskitError("Invalid input data format for Statevector")
94 # Check that the input is a numpy vector or column-vector numpy
95 # matrix. If it is a column-vector matrix reshape to a vector.
96 ndim = self._data.ndim
QiskitError: 'Invalid input data format for Statevector'
