Jun 11, 2024 | 8 min read

Estimación de fase y aplicaciones

\( \newcommand{\bra}[1]{\langle #1|} \) \( \newcommand{\ket}[1]{|#1\rangle} \) \( \newcommand{\braket}[2]{\langle #1|#2\rangle} \) \( \newcommand{\i}{{\color{blue} i}} \) \( \newcommand{\Hil}{{\cal H}} \) \( \newcommand{\cg}[1]{{\rm C}#1} \) \( \newcommand{\det}{{\rm det}}\)

Show code cell source Hide code cell source

%run ../macro_tQ.py
import sys
sys.path.append('../')
import macro_tQ as tQ

Estimación Cuántica de Fase

Cuando se construya un computador cuántico capaz de realizar una Transformada de Fourier Cuántica, una de las aplicaciones más frecuentes será la Estimación Cuántica de Fase. Veamos cómo funciona.

Sea \(U\) un operador unitario y \(\ket{u}\) un autovector del espacio de Hilbert \(\Hil\) de dimensión \(n\).

Lema:

por ser unitario, su autovalor es una fase compleja

\[ U \ket{u} = e^{2\pi i\varphi} \ket{u} \]

Demostración

Una forma rápida de demostrar esto es analizar el determinante de la matriz \(U\) asociada al operdor. El determinante del producto de dos matrices tiene una propiedad importantísima, y es que factoriza

\[ \det \, (A B) = (\det A) (\det B) \]

De esta propiedad se deduce, como ya se vio en el capítulo de operadores, que el determinante de un operador es independiente de la base (lo mismo le pasaba a la traza). También se deduce que el determinante de un operador unitario es una fase. Por un lado tenemos que

\[ \det (U U^\dagger) = (\det U)(\det U^{*t}) = (\det U)(\det U)^* = |\det U|^2 \]

Por otro

\[ \det (U U^\dagger) = \det (U U^{-1}) = \det I = 1 \]

Es decir, el módulo de \(\det U\) es igual a 1, y por tanto \(\det U = e^{i\varphi}\), una fase. En la base en la que \(U\) es diagonal, esta fase es el producto de los elementos de la diagonal. Por tanto, todos los autovaleres deben ser fases

\[ e^{i\varphi} = e^{i(\lambda_1 + \lambda_2 +...+\lambda_n)} \]

s>

\(\Rightarrow~\) Promesa: podemos preparar el autoestado \(\ket{u}\) y aplicar el operador \(U\) tantas veces como sea necesario

\(\Rightarrow~\) Problema: calcular la mejor aproximación posible a \(\varphi\).

Notar

Los autovalores \(\lambda = e^{i2\pi \varphi}=e^{i2\pi (\varphi+n)}\) son iguales, para cualquier \(n\in {\mathbb Z}\) entero. Por tanto, será suficiente considerar valores de \(\varphi\) en el intervalo

\[\varphi \in [0,1)\]

para generar todos los posibles autovalores \(\lambda\) distintos

El circuito QPE (“Quantum Phase Estimation”) viene representado en la figura, donde el primer registro tiene dimensión \(t\) y la entrada es el estado \(\ket{0}_t\otimes \ket{u}\).

• \(t\) es la dimensión del primer registro, o registro de contaje. Su valor controlará la precisión de nuestra aproximación a \(\varphi\).

• \(n\) es la dimensión del espacio \(\Hil\) al que pertenece el vector \(\ket{u}\), sobre el que actúa \(U\).

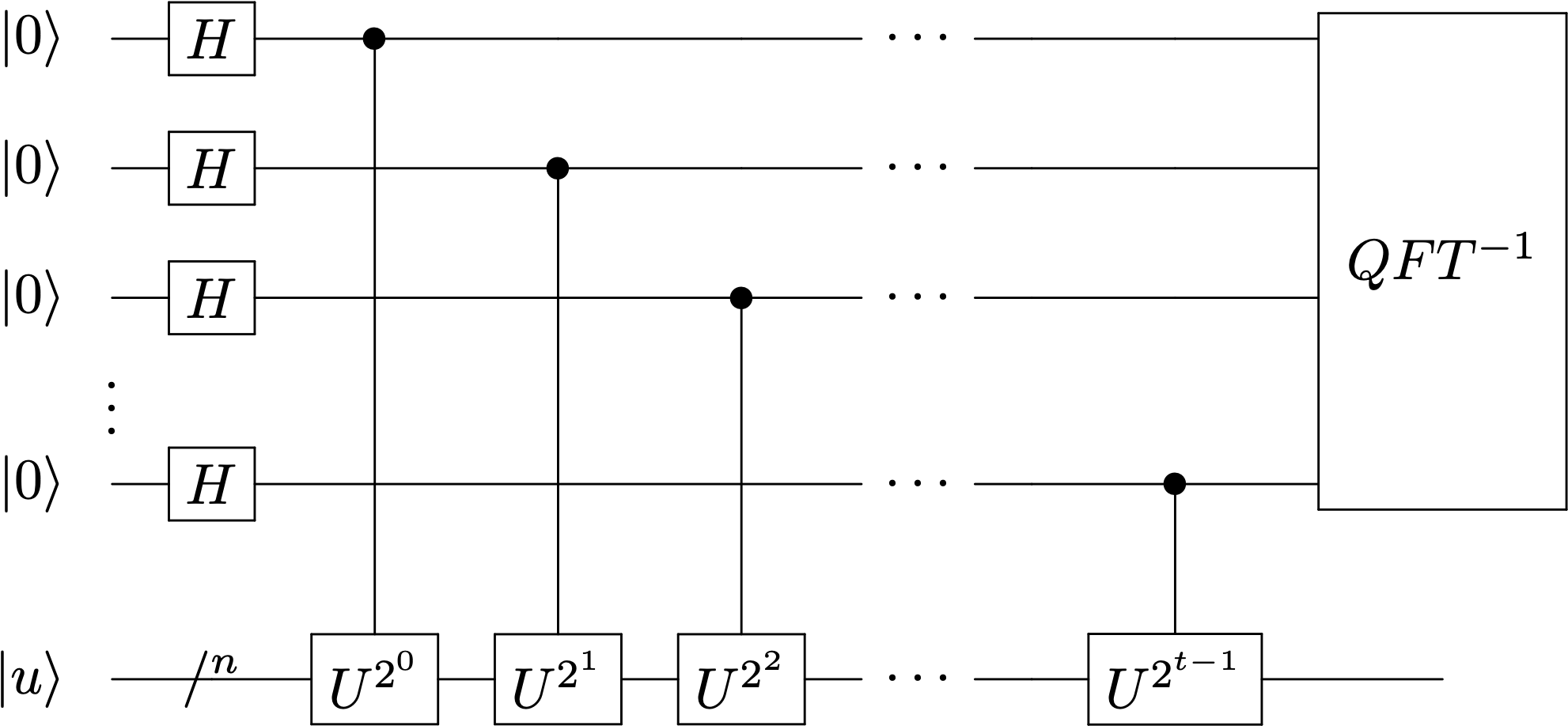
Si el primer registro tiene \(t\) cúbits \(\{\ket{y}\}\) con \(y \in S_t = 0,1,... 2^t-1\) el estado que genera el circuito justo antes de la transformada de Fourier es el siguiente

\[\begin{eqnarray*} \ket{0}_t \otimes \ket{u} ~ &\stackrel{H^{\otimes t}}{\longrightarrow} & ({H^{\otimes t}} \ket{0}_t)\otimes \ket{u} = \frac{1}{2^{t/2}} \sum_{y_0...y_{t-1}=0,1}\ket{y_{t-1}}...\ket{y_0}\otimes \ket{u} \\ \rule{0mm}{10mm} &\stackrel{\prod_{i=0}^{t-1} \cg{U}^{2^i}}{\longrightarrow} & \frac{1}{2^{t/2}} \sum_{y_0...y_{t-1}=0,1}\ket{y_{t-1}}...\ket{y_0}\otimes U^{y_{t-1}2^{t- 1}}...U^{y_0 2^{0}} \ket{u} \\ \rule{0mm}{10mm} && = \frac{1}{2^{t/2}} \sum_{y\in S_t} \ket{y} \, U^{y_{t-1}2^{t-1}+ \ldots +y_0 2^0}\ket{u} \\ && = \, \frac{1}{2^{t/2}} \sum_{y\in S_t} \ket{y} \, U^y\ket{u} \rule{0mm}{10mm} \end{eqnarray*}\]

La clave: por ser \(\ket{u}\) un autoestado de \(U\), se produce un retroceso de fase

\[\begin{eqnarray*} \frac{1}{2^{t/2}} \sum_{y\in S_t} \ket{y} U^{y}\ket{u} &~= ~& \frac{1}{2^{t/2}} \sum_{y\in S_t} \ket{y} \otimes e^{2\pi i \varphi y} \ket{u} = \frac{1}{2^{t/2}} \sum_{y\in S_t}e^{2\pi i \varphi y} \ket{y} \otimes \ket{u} \\ \rule{0mm}{12mm} &~\equiv ~& \frac{1}{2^{t/2}} \sum_{y\in S_t} e^{2\pi i (2^t \varphi) y/2^t} \ket{y}\otimes \ket{u} \label{fase1} \end{eqnarray*}\]

Como de costumbre, el segundo registro ya ha realizado su labor y podemos medirlo o ignorarlo (es una ancilla). De modo que nos vamos a concentrar en el registro de contaje, de \(t\) cúbits. Para completar el circuito sólo nos faltaría aplicar la transformada de Fourier inversa. Antes de hacerlo vamos a notar que \(2^t\varphi\) es, en general, un número real. Vamos a escribirlos separando la parte entera \(a\), de la mantisa \(\delta\)

\[ 2^t \varphi =a + \delta \]

Ejemplo

Supongamos que la fase que queremos hallar sea: \(\varphi = 0.4375 \in [0,1) \). Entonces

• \( 2^2 \varphi = 1.75 \Rightarrow a=1~,~\delta = 0.75\)

• \( 2^3 \varphi = 3.5~ \Rightarrow a=3~,~\delta = 0.5\)

• \( 2^4 \varphi = 7 ~~~ \Rightarrow a=7~,~\delta = 0\)

Cuando \(t=4\) obtenemos un número entero. En realidad ya lo habíamos cocinado así \(0.4375 = 7 / 2^{4}\). Pero si \(\varphi\) es irracional no existirá ningún \(t\) para el cuál \(2^t\varphi\) no tenga mantisa.

Ahora aplicamos la TFC inversa, que es igual a la adjunta, al primer registro

\[\begin{eqnarray*} U^\dagger_{TFC} \frac{1}{\sqrt{2^t}} \sum_{y=0}^{2^t-1} e^{2\pi i \, (a + \delta) y/2^t} \ket{y} &~~\stackrel{\hbox{linealidad}}{=} ~~&\frac{1}{\sqrt{2^t}} \sum_{y=0}^{2^t-1} e^{2\pi i \, (a + \delta) y/2^t} U^\dagger_{TFC} \ket{y} \\ \rule{0mm}{10mm} ~&=&~ \frac{1}{\sqrt{2^t}} \sum_{y=0}^{2^t-1} e^{2\pi i (a + \delta) y/2^t}\frac{1}{\sqrt{2^t}}\left( \sum_{x=0}^{2^t-1}e^{-2\pi i yx/2^t}\ket{x} \right) \\ \rule{0mm}{10mm} ~&=&~ \frac{1}{2^{t}} \sum_{x=0}^{2^t-1} \sum_{y=0}^{2^t-1} e^{2\pi i (a + \delta -x) y/2^t} \ket{x} \\ \rule{0mm}{8mm} &~ \equiv ~ & \ket{\Phi} \end{eqnarray*}\]

\(\ket{\Phi}\) es el estado final en el registro de contaje. Vamos a analizar su composición, separando dos casos posibles para \(\varphi\).

• Supongamos que \(\underline{\delta = 0}\). Es decir, que \(2^t\varphi\) sea un entero \(a\in S_t = \{0, \ldots, 2^t-1\}\).

Entonces el resultado sería exactamente \(\ket{\Phi} = \ket{a} = \ket{2^t\varphi}\)

\[\begin{eqnarray*} \ket{\Phi} &=& \sum_{x=0}^{2^t-1} \frac{1}{2^{t}} \left(\sum_{y=0}^{2^t-1} e^{2\pi i (a-x) y/2^t} \right)\ket{x} \\ \rule{0mm}{10mm} &=& \sum_{x=0}^{2^t-1} \frac{1}{2^{t}} \left(2^t \delta_{x,a} \right)\ket{x}\\ \rule{0mm}{8mm} &=& \ket{a} \end{eqnarray*}\]

Midiendo el primer registro obtendríamos, con probabilidad 1, el registro binario del número \(a\in[0, 2^t-1]\)

Escribiendo \(a\) en base decimal, y normalizando por \(2^t\), recuperaríamos la fase buscada de forma exacta

\[ \varphi = \frac{a}{2^t} \in [0,1) \]

• Supongamos ahora que \(\underline{\delta \neq 0}.~\) Es decir, \(2^t\varphi\) no es un entero.

En este caso la transformada de Fourier inversa no produce un único estado, sino una superposición

\[ \ket{\Phi} = \sum_{x=0}^{2^t-1} \left( \frac{1}{2^{t}}\sum_{y=0}^{2^t-1} e^{2\pi i (a + \delta -x) y/2^t} \right) \ket{x} = \sum_{x=0}^{2^t-1} f(x) \ket{x} \]

Las amplitudes \(f(x)\) están evaluadas con \(x\in S_t\) números enteros. Pero la expresión es valida para cualquier número real \(x\in {\mathbb R}\).

Una medida dará el registro binario de un número entero \(x \in [0,2^t-1)\) con distribución de probabilidad \(p(x) = |f(x)|^2\) centrada en \(a=[2^t\varphi]\).

Por tanto, con una sucesión de tiradas podríamos reconstruir la distribución de probabilidad, y su media sería el valor buscado de \(2^t\delta\).

Distribución de probabilidad

Para una mantisa fija, \(\delta \Rightarrow 2^t\varphi = a+\delta\) las distintas medidas del estado resultante \(\ket{x}\) se distribuirán en el torno a \(\ket{a} \).

Escribiendo \(\ket{x}=\ket{a+l}\) podemos obtener la distribución de probabilidad \(p(x) = p(\delta, l)\) de medir \(\ket{x}=\ket{a+l}\)

\[\begin{eqnarray*} p(\delta, l) = |\braket{a+l}{\Phi}|^2 ~~&=&~~ \left\vert \, \, \frac{1}{2^{t}}\sum_{x=0}^{2^t-1} \sum_{y=0}^{2^t-1} e^{2\pi i (\delta + a -x) y/2^t} \braket{a+ l}{x} \, \right\vert^2 ~~ \stackrel{x= a + l}{=} ~~ \frac{1}{2^{2t}} \left\vert \, \sum_{y=0}^{2^t-1} \left(e^{2\pi i (\delta-l) /2^t}\right)^y \, \right\vert^2 \\ \rule{0mm}{10mm} &=& ~~ \frac{1}{2^{2t}} \left\vert\, \frac{1- e^{2\pi i \, (\delta-l) }}{1- e^{2\pi i (\delta-l)/2^t}} \, \right\vert^2 ~= ~ \frac{1}{2^{2t}} \left\vert \, \frac{\sin \pi (\delta-l)}{\sin (\pi(\delta-l)/2^t)} \, \right\vert^2 \, \\ \end{eqnarray*}\]

donde en la última línea hemos sumado una serie geométrica. Vamos a graficar esta función para distintos valores de \(\delta\)

t=4
deltalist = np.array([0.1,0.3,0.5,0.7])
shift=-2**(t-1)+1
xlist = np.arange(shift,2**(t)-1+shift)

for delta in deltalist:
    plist = [(1/2**(2*t))*(np.sin(np.pi*(delta-l))/np.sin(np.pi*(delta-l)/2**t))**2 for l in xlist]
    plt.plot(xlist,plist, label=f'delta = {delta}')

plt.xlabel(r'$x$')
plt.ylabel(r'$p(\delta, t)$')
plt.legend()
plt.show()

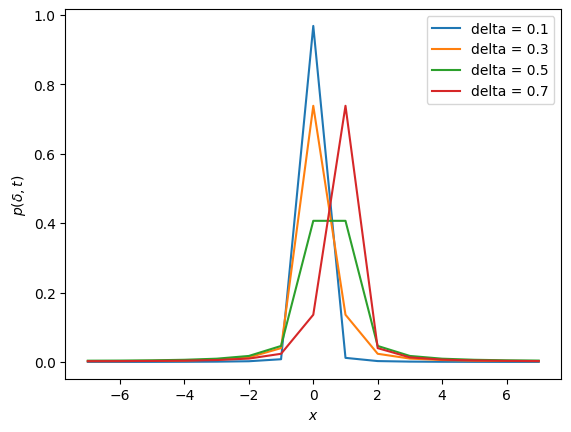
El registo de contaje sólo puede dar \(2^t\) valores distintos que hemos escogido en el intervalo \(l \in [\hbox{shift},\, 2^{t}-1+\hbox{shift})\). Puedes mover shift.

• Cuando \(\delta\ll 1\) la distribución está muy picada en torno a \(l=0\), es decir \(x=a\).

• A medida que \(\delta\) se acerca a \(0.5\) el valor máximo de \(p(\delta,l)\) diminuye, pero nunca es menor que \(0.405\).

• Cuando \(\delta >0.5\) la distribución empieza a mostrar que el valor más aproximado para \(2^t\varphi\) es el siguiente, con \(l=1\). Es decir \(x=a+1\).

Demostración

Que la probabilidad nunca es menor de 0.405 en su máximo se puede probar analíticamente

\[ \frac{1}{2^{2t}} \left\vert \, \frac{\sin \pi (\delta-l)}{\sin (\pi(\delta-l)/2^t)} \, \right\vert^2 \, \geq \frac{1}{2^{2t}} \left(\frac{2 (\delta-l)}{\pi(\delta-l)/2^t }\right)^2 = \left(\frac{2}{\pi}\right)^2 \sim 0.405 \]

donde hemos usado que \(\pi x\geq \sin(\pi x) \geq 2 x\) para \(x\in [ 0,\pi/2 ]\).

Si varías \(t\) comprobaras que: la anchura \(t\) del circuito de contaje determina la dispersion de la curva de probabilidad en torno al valor medio. A mayor valor de \(t\), la distribución se vuelve más estrecha.

Si queremos acotar por debajo la probabilidad de encontrar un valor de \(x\) que aproxime el valor correcto de \(2^t\varphi\) dentro de una cierta tolerancia, debemos aumentar \(t\) los suficiente. El siguiente teorema aclara definitivamente cuánto hay que hacerlo

Teorema:

El algoritmo QPE (Quantum Phase Estimation) es capaz de producir

• una estimación \(x\) de orden \(k\) para la fase \(\varphi\) (en el sentido de que \(|\varphi- x/2^t |<2^{-k}\))

• con una probabilidad \(1-\epsilon\)

tomando una anchura del registro de contaje, \(t\), suficientemente alta

\[ t \geq k + \left[ \log\left(1 + \frac{1}{2\epsilon}\right) \right] \label{tedeene} \]

Demostración

ver Nielsen Chuang p. 224).

Ejemplo

Vamos a estudiar esta distribución analizando el operador unitario de fase

\[\begin{split} U = \begin{bmatrix} e^{2\pi i \phi_0} & 0 \\ 0 & e^{2\pi i\phi_1}\end{bmatrix} \end{split}\]

que tiene por autoestados \(\ket{0}\) y \(\ket{1}\) con autovalores \(e^{2\pi\phi_0}\) y \(e^{2\pi \phi_1}\) respectivamente.

Para programar el oráculo que implementa este operador notamos que

\[\begin{split} U = \begin{bmatrix} e^{2\pi \phi_0} & 0 \\ 0 & e^{-2\pi i\phi_0}\end{bmatrix} \begin{bmatrix} 1 & 0 \\ 0 & e^{2\pi i(\phi_0+\phi_1)}\end{bmatrix} = R_z(\theta = -4\pi \phi_0) \cdot P(\theta = 2\pi (\phi_1+\phi_0)) \end{split}\]

El circuito requiere la versión controlada \(\cg U^k\) de potencias de este operador

def c_Uop(phi0,phi1,power):
    U = QuantumCircuit(1)        
    for _ in range(power):
        U.rz(-phi0*4*np.pi,0)
        U.p((phi1+phi0)*2*np.pi,0)
    U = U.to_gate()
    U.name = "c_U(%f ,%f)^%i" % (np.round(phi0,5), np.round(phi1,5),power)
    U = U.control()
    return U

Para poner a prueba el algoritmo vamos a por seleccionar unos valores de \(\phi_i = (\phi_0,\phi_1)\) de la forma

\[\phi_i = (a_i + \delta_i) 2^{-t}\]

t_seed=3

a0 = 2.
delta0 = 0.2
phi0 = (a0+delta0)*2.**(-t_seed) 

a1 = 3.
delta1 = 0.
phi1 =(a1+ delta1)*2.**(-t_seed) 

print('phi0=', phi0, ' ->   2^t*phi0 = a0 + delta0 = ', 2**t_seed*phi0 , ' , a0 =' ,int(2**t_seed*phi0), '=>', format(int(2**t_seed*phi0),'b').zfill(t_seed) )
print('phi1=', phi1, ' ->   2^t*phi1 = a1 + delta1 = ', 2**t_seed*phi1 , ' , a1 =' ,int(2**t_seed*phi1), '=>', format(int(2**t_seed*phi1),'b').zfill(t_seed) )

phi0= 0.275  ->   2^t*phi0 = a0 + delta0 =  2.2  , a0 = 2 => 010
phi1= 0.375  ->   2^t*phi1 = a1 + delta1 =  3.0  , a1 = 3 => 011

Construimos el circuito QPE

from qiskit import QuantumCircuit, QuantumRegister, ClassicalRegister

t = 6 # la dimensión del registro de evaluación 
n = 1 # la dimensión del espacio de representación del opeador U

qrt=QuantumRegister(t,name="t")
qra=QuantumRegister(n,name="qr_U") # aquí 1 es la dimensión del espacio en el que opera U
crt=ClassicalRegister(t)

qpe = QuantumCircuit(qrt,qra,crt)   

##########################################################################
#inicializamos la ancilla en un autoestado |u> =|0> o |u> = |1>
#qpe.x(qra)   
##########################################################################


qpe.h(range(t))
qpe.barrier()

# aplicamos los operadores controlados c-U^j 
for j in range(t):
    qpe.append(c_Uop(phi0,phi1,2**j),[qrt[j]]+qra[:])
    

qpe.barrier()

# aplicamos la QFT^-1 que está definida en macro.py 
qpe.append(TFC_adj(t),qrt)

qpe.measure(qrt,crt)

qpe.draw(output="mpl")

/opt/anaconda3/envs/TalentQ/lib/python3.11/site-packages/qiskit/visualization/circuit/matplotlib.py:266: FutureWarning: The default matplotlib drawer scheme will be changed to "iqp" in a following release. To silence this warning, specify the current default explicitly as style="clifford", or the new default as style="iqp".
  self._style, def_font_ratio = load_style(self._style)

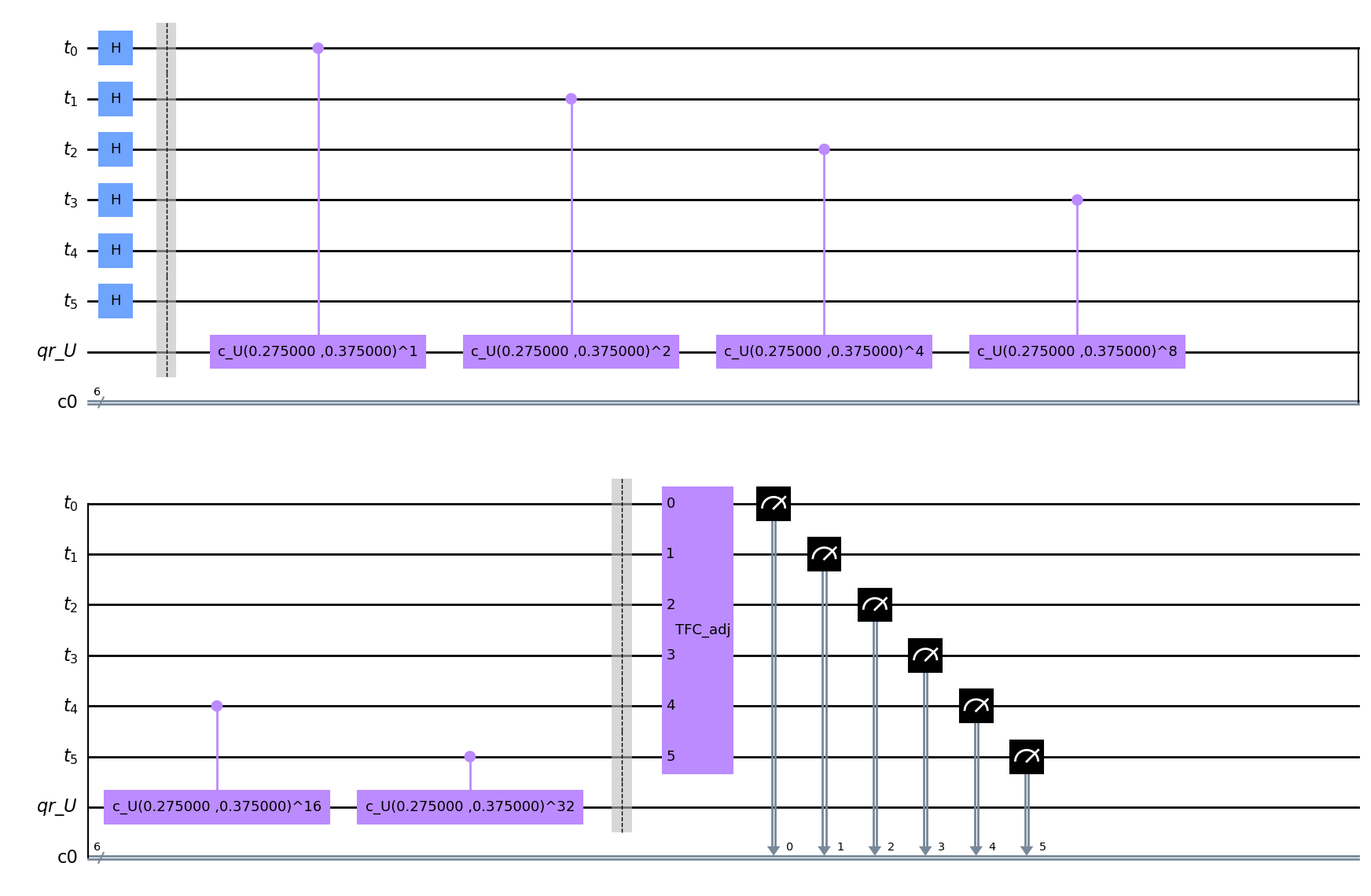
'ejecutamos el circuito'
from qiskit.primitives import Sampler
from qiskit.visualization import plot_histogram, plot_bloch_multivector

nshots = 1000
dist = Sampler().run(qpe,shots=nshots).result().quasi_dists[0]
counts = tQ.dist2counts(dist,t,nshots)

plot_histogram(counts)

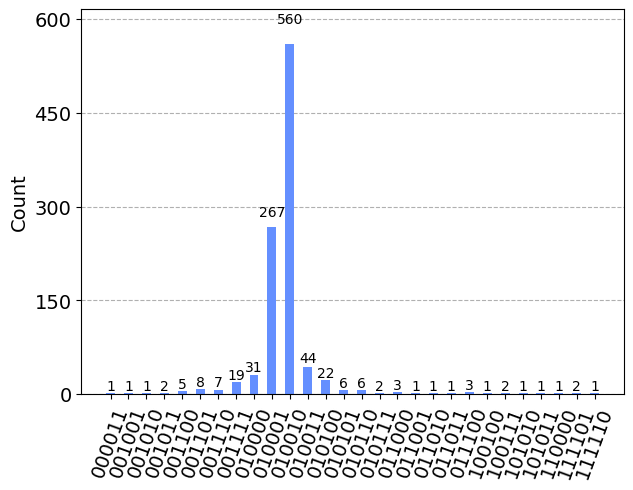
De aquí extraemos la aproximación que hemos obtenido.

max(counts, key=counts.get)

'010010'

a_resultante = int(max(counts, key=counts.get),2)

# Seleccionamos el autovalor asociado a |u> 
phi = phi0  # si |0>
#phi = phi1   # si |1>

print('el valor de phi original era =', phi)

print('la mejor aproximación al valor verdadero es a/2^t =', a_resultante*2**(-t))

print('el error relativo es delta/(2^t phi) =', (phi -a_resultante*2**(-t))/phi)

el valor de phi original era = 0.275
la mejor aproximación al valor verdadero es a/2^t = 0.28125
el error relativo es delta/(2^t phi) = -0.022727272727272645

Ejercicio

vuelve a ejecutar el circuito cambiando el valor de \(\varphi_0\).

¿y si no podemos preparar un autoestado?

Una de las premisas usadas en la sección anterior es la posibilidad de preparar el autoestado \(\ket{u}\) de \(U\)

En caso contrario, ¿qué resultado obtenemos después de usar el circuito de estimación cuántica de fase?. Vamos a aprovechar el hecho de que el conjunto \(\{\ket{u_i}\}\) de los autoestados de \(U\)

\[U\ket{u_i} = e^{2\pi i\varphi_i}\ket{u_i}\]

forman una base del espacio de Hilbert \(\Hil\). Apliquemos el circuito anterior a un vector arbitrario \(\ket{b}\). Genéricamente dicho vector admitirá una expansión de la forma

\[ \ket{b} = \sum_{i=1}^N c_i \ket{u_i} \]

Debido a la linealidad del circuito QPE, a la salida del mismo encontraremos una combinación lineal de estados de la forma

\[\begin{eqnarray*} U_{QPE}\, :\,\ket{0}_t \left(\sum_{i=1}c_i\ket{u_i}\right) &=& \sum_{i=1}c_i U_{QPE}\left(\ket{0}_t\ket{u_i} \rule{0mm}{6mm}\right) \\ &=& \sum_{i=1}^N c_i \ket{\Phi_i}\ket{u_i} \\ &=& \sum_{i\in S_n}\sum_{x\in S_t} c_i \ket{x}\braket{x}{\Phi_i}\ket{u_i} \\ &=& \sum_{i\in S_n}\sum_{x\in S_t} c_i \braket{x}{\Phi_i} \ket{x}\ket{u_i} \end{eqnarray*}\]

Midiendo en el primer registro obtendremos un número entero \( x \) asociado a un vector \(\ket{x}\) con probabilidad

\[ p(x) = \sum_i |c_i|^2 |\braket{x}{\Phi_i}|^2 = \sum_i |c_i|^2 p(\delta_i,l_i) \]

En resumen: la probabilidad \(p(x)\) es una suma ponderada de distribuciones \(p(\delta_i,l_i) = |\braket{x}{\Phi_i}|^2\) con \(x = a_i + l_i\) picadas en torno \(l_i = 0\).

Si \(t\) se escoge como en el teorema descrito anteriormente, el resultado será una aproximación \(x\) a alguno de los valores \(2^t\varphi_i\) con una probabilidad de acierto de, al menos, \(|c_i|^2 (1-\epsilon)\).

Ejemplo:

Vamos a correr el circuito QPE inicializando para una combinaciones \(\ket{b} = \cos \theta/2 \ket{0} + \sin \theta/2 \ket{1}= R_y(\theta)\ket{0}\) de autoestados de \(P(\varphi)\).

t_seed = 3

a0 = 1.
delta0 = 0.1
phi0 = (a0+ delta0)*2.**(-t_seed) 

a1 = 3.
delta1 = 0.1
phi1 =(a1+ delta1)*2.**(-t_seed) 

print('phi0=', phi0, ' ->   2^t*phi0 = a0 + delta0 = ', 2**t_seed*phi0 , ' , a0 =' ,int(2**t_seed*phi0), '=>', format(int(2**t_seed*phi0),'b').zfill(t_seed) )
print('phi1=', phi1, ' ->   2^t*phi1 = a1 + delta1 = ', 2**t_seed*phi1 , ' , a1 =' ,int(2**t_seed*phi0), '=>', format(int(2**t_seed*phi1),'b').zfill(t_seed) )

phi0= 0.1375  ->   2^t*phi0 = a0 + delta0 =  1.1  , a0 = 1 => 001
phi1= 0.3875  ->   2^t*phi1 = a1 + delta1 =  3.1  , a1 = 1 => 011

from qiskit import QuantumCircuit, QuantumRegister, ClassicalRegister

t = 6 # la dimensión del registro de evaluación 
n = 1 # la dimensiónd el espacio de representación del opeador U

qrt=QuantumRegister(t,name="t")
qra=QuantumRegister(n,name="qr_U") # aquí 1 es la dimensión del espacio en el que opera U
crt=ClassicalRegister(t)

qpe = QuantumCircuit(qrt,qra,crt)   

##########################################################################
#inicializamos la ancilla en una combinación cos(th/2)|0> + sin(th/2)|1>
theta = 2*np.pi*0.15 
qpe.ry(theta,qra) 
##########################################################################

qpe.h(range(t))
qpe.barrier()

# aplicamos los operadores controlados c-U^j 
for j in range(t):
    qpe.append(c_Uop(phi0,phi1,2**j),[qrt[j]]+qra[:])
#    qpe.cp(2*np.pi*phi1*(2**j), qrt[j], qra); # This is C-U
    

qpe.barrier()

# aplicamos la QFT^-1 que está definida en macro.py 
qpe.append(TFC_adj(t),qrt)

# podemos hacerlo usando la librería de qiskit 
#from qiskit.circuit.library import QFT
#qpe.append(QFT(len(qr),do_swaps=True).inverse(),qr)


qpe.measure(qrt,crt)

qpe.draw(output="mpl")

/opt/anaconda3/envs/TalentQ/lib/python3.11/site-packages/qiskit/visualization/circuit/matplotlib.py:266: FutureWarning: The default matplotlib drawer scheme will be changed to "iqp" in a following release. To silence this warning, specify the current default explicitly as style="clifford", or the new default as style="iqp".
  self._style, def_font_ratio = load_style(self._style)

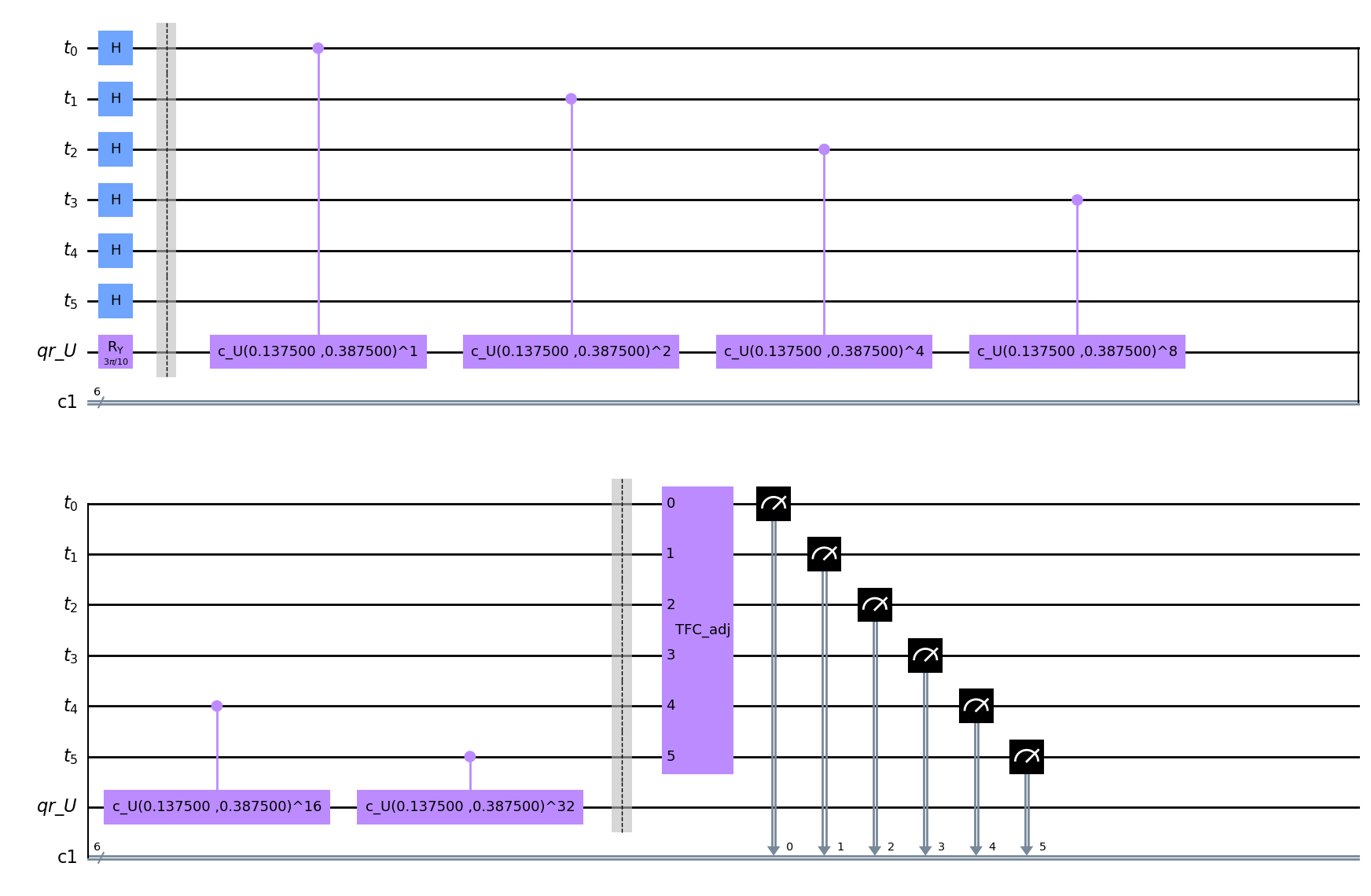
'ejecutamos el circuito'
from qiskit.primitives import Sampler
from qiskit.visualization import plot_histogram, plot_bloch_multivector

nshots = 1000
dist = Sampler().run(qpe,shots=nshots).result().quasi_dists[0]
counts = tQ.dist2counts(dist,t,nshots)

plot_histogram(counts)

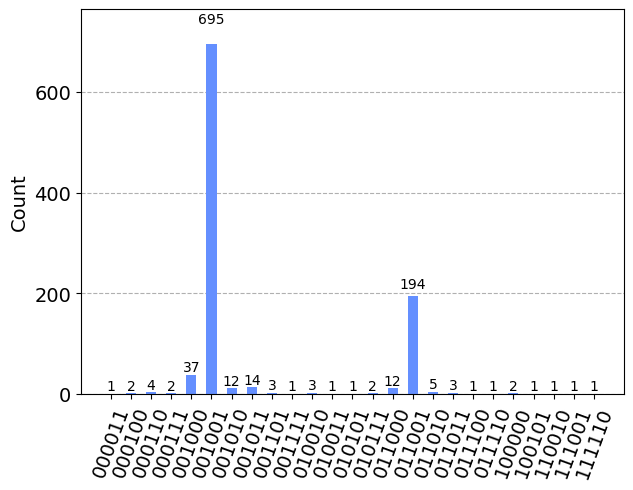
Orden modular

A continuación vamos a estudiar un importante problema matemático que está debajo del algoritmo de Shor, que puede formularse como un problema de estimación de fase.

Definición: Orden modular

Sean \(m,N \in {\mathbb N}\) dos enteros \(m<N\) coprimos (sin divisores comunes). Definimos el orden de \(m\) módulo \(N\) como el menor entero positivo, \(r\), tal que \(m^r = 1\) mod\(N\).

Promesa: \(U\) es el oráculo de una función modular \((m,N)\) de orden \(r\).

Problema: hallar \(r\) con el número mínimo de consultas.

'Ejemplo'
{2,4,7,8,11,13}   # comprimos con 15
m=7
N=15
[m**i%N for i in range(17)]

[1, 7, 4, 13, 1, 7, 4, 13, 1, 7, 4, 13, 1, 7, 4, 13, 1]

Nota

• En general, si \(N=2^n\), clásicamente no existen algoritmos capaces de resolver este problema en un número de pasos que sea polinómico en \(n\). Por el contrario, verificar si un \(r\) es solución es fácil. Nos hallamos ante un problema de tipo NP.

• Como \(m^r = 1 = m^0\), a partir de ese momento la serie de valores \(\{m^0,m^1,\ldots m^{r-1}\}\) se repite. Por tanto, hallar el orden modular de \(m\) módulo \(N\) es lo mismo que hallar la periodicidad de la función \(f(x) = m^x\, \)mod\(N\).

Si tratamos de fabricar un oráculo para el operador unitario \(U_f:\ket{x}\ket{y} \to \ket{x}\ket{m^x y \,{\rm mod} N}\) nos encontraremos con una complejidad exponencial. En este caso, sin embargo, la estructura del problema permite una simplificación.

Supongamos que sabemos implementar un oráculo \(U ; \Hil_n \to \Hil_n \) que actúa en la forma siguiente sobre la base \(\{\ket{y}\}\) donde \(y \in S_n = {0,1,...,N-1}\)

\[ U\ket{y } = \ket{m y \,{\rm mod} N} \]

La composición \(U^x = \underbrace{U\cdot U \cdots U}_{x}\) genera todos los vectores que buscamos

\[ U^x\ket{y } = U^{x-1}\ket{m y \,{\rm mod} N} = U^{x-2}\ket{m^2 y \,{\rm mod} N} = ... = \ket{m^x y \,{\rm mod} N} \]

El orden de \(m\) mod\(N\) es claramente el número \(r\) tal que

\[U^{r }\ket{y} = \ket{m^r y \,{\rm mod} N} = \ket{y}\]

Con \(U\) podríamos implementar la función \(f(x) = m^x{\rm mod} N\) en la forma

\[ U_f \ket{x}\ket{1} = \ket{x}U^x\ket{1} = \ket{x}\ket{m^x \, {\rm mod} N } \]

y buscar la periodicidad de \(f(x+r) = f(x)\) siguiento el método de la lección anterior.

La acción de \(U_f\) parece mucho a la de un operador controlado \(\cg{U}\ket{x}\ket{y} = \ket{x}U^x\ket{y}\). Sin embargo ahora \(x = 0,1,...,2^t-1\) es un entero.

Este operador controlado es exactamente el que se utiliza en el circuito de QPE. Con esta observación vamos a aplicar el método de Estimación Cuántica de Fase (QPE) al operador \(U\)

Recordemos que dicho método nos pide evaluar el operador \(U\) sobre sus autovectores \(U\ket{u} = e^{i\varphi}\ket{u}\). Pero… ¿conocemos estos autovectores? Resulta que, si conociésemos \(r\) podríamos construir el siguiente conjunto de \(r\) vectores \(\ket{u_s}\) con \(s=0,...,r-1\)

\[ \ket{u_s} = \frac{1}{\sqrt{r}} \sum_{j=0}^{r-1} e^{-2\pi i \frac{s }{r}j} U^j\ket{1} \]

Nótese el papel importante que juega ahora el estado de la base \(\ket{1} = \ket{0...01}\)

Teorema:

Los vectores \(\{\ket{u_s}\}\) forman un conjunto de autovectores de \(U\) con autovalores \(e^{2\pi i s/r}~\). Es decir

\[ U\ket{ u_s} = e^{2 \pi i\varphi_s} \ket{u_s} \]

con $\( \varphi_s = s/r~~~~~~ s=0,...,r-1 \)$

Demostración

(25)\[\begin{eqnarray} U \ket{u_s} &=& \frac{1}{\sqrt{r}} \sum_{j=0}^{r-1} e^{-2\pi i s j/r} U^{j+1}\ket{1} \nonumber\\ &=& e^{2\pi i \frac{s}{r}} \frac{1}{\sqrt{r}} \sum_{j=0}^{r-1} e^{-2\pi i s (j+1)/r} U^{j+1}\ket{1} = e^{2\pi i \frac{s}{r}} \frac{1}{\sqrt{r}} \sum_{j=0}^{r-1} e^{-2\pi i s j/r} U^{j}\ket{1} \nonumber\\ &=& e^{2\pi i s/r} \ket{u_s}\, . \rule{0mm}{8mm} \end{eqnarray}\]

El problema es que \(r\) es, precisamente, ¡el dato que queremos encontrar! Una observación importante que nos permite soslayar esta dificultad es la siguiente: vamos a tomar una combinación homogénea de los autoestados \(\ket{u_s}\)

(26)\[\begin{eqnarray} \frac{1}{\sqrt{r}} \sum_{s=0}^{r-1}\ket{u_s} &=& \frac{1}{\sqrt{r}} \sum_{s=0}^{r-1} \left( \frac{1}{\sqrt{r}} \sum_{j=0}^{r-1} e^{-2\pi i sj/r} U^{j}\ket{1} \right) ~=~ \frac{1}{r} \sum_{j=0}^{r-1} \left( \sum_{s=0}^{r-1}e^{-2\pi i sj/r} \right)U^{j}\ket{1} \nonumber\\ \rule{0mm}{12mm} &=& \frac{1}{r} \sum_{j=0}^{r-1} \, (r \delta_{j,0}) \, U^{j}\ket{1} = U^0\ket{1} \nonumber\\ \rule{0mm}{10mm} &=& \ket{1} \end{eqnarray}\]

¡El resultado es asombrosamente simple!: si inicializamos el circuito de estimación de fase con el estado \(\ket{0}_t\ket{1}_n\) a la salida obtendremos una superposición uniforme

\[ U_{QPE} : \ket{0}_t \otimes \ket{1}_n ~ \to ~ \frac{1}{\sqrt{r}}\sum_{s=0}^{r-1} \ket{x_s}\otimes\ket{u_s} \]

donde \(x_s = 2^t s/r\) siempre que \(t\) se haya elegido de forma que todos los número \(~2^t s/r \in {\mathbb Z}\) sean enteros

¡A programar!

Necesitamos un oráculo que implemente la operación

\[U\ket{y} = \ket{m y \,{\rm mod} N} \]

El siguiente código implementa este oráculo para \(N=15\) y \(m\in \{2,4,7,8,11,13\}\) coprimos, y lo convierte en una puerta controlada

from qiskit import QuantumCircuit, QuantumRegister, ClassicalRegister

def c_amod15(m, power):
    """Controlled multiplication by a mod 15"""
    if m not in [2,4,7,8,11,13]:
        raise ValueError("'a' must be 2,4,7,8,11 or 13")
    U = QuantumCircuit(4)        
    for iteration in range(power):
        if m in [2,13]:
            U.swap(2,3)
            U.swap(1,2)
            U.swap(0,1)
        if m in [7,8]:
            U.swap(0,1)
            U.swap(1,2)
            U.swap(2,3)
        if m in [4, 11]:
            U.swap(1,3)
            U.swap(0,2)
        if m in [7,11,13]:
            for q in range(4):
                U.x(q)
#    print(U)
    U = U.to_gate()
    U.name = "%i^%i mod 15" % (m, power)
    c_U = U.control()
    return c_U

c_amod15(4,3 ).definition.draw('mpl')

/opt/anaconda3/envs/TalentQ/lib/python3.11/site-packages/qiskit/visualization/circuit/matplotlib.py:266: FutureWarning: The default matplotlib drawer scheme will be changed to "iqp" in a following release. To silence this warning, specify the current default explicitly as style="clifford", or the new default as style="iqp".
  self._style, def_font_ratio = load_style(self._style)

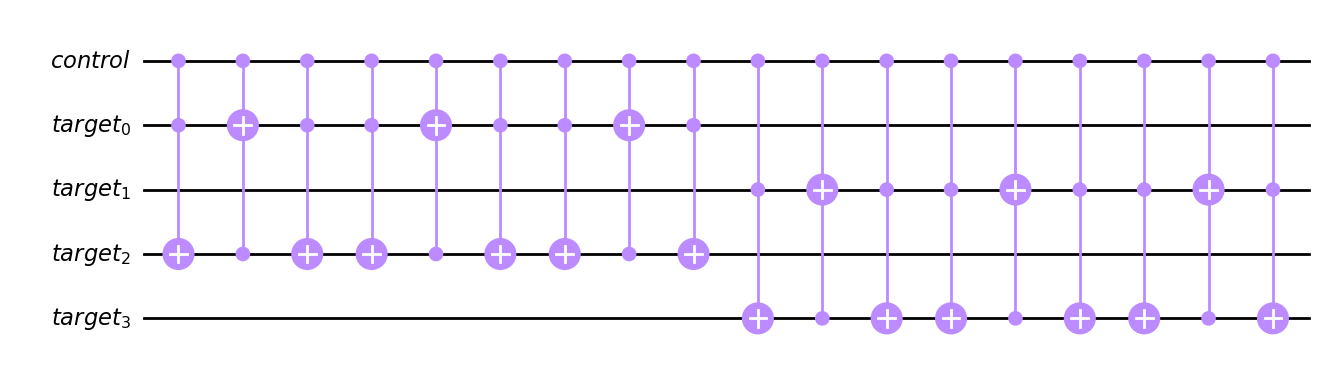
Nota

• Función definida en Qiskit Textbook

• No hay una prescripción general para valores arbitrarios de \(m\) y \(N\) que no pase por escribir toda la tabla de verdad. No queremos eso porque sabemos que no es eficiente.

Ejercicio

Construye un circuito con esta puerta y verifica que reproduce la lista \(m^x\) mod 15 con \(x=0,1,2,...\)

from qiskit import QuantumCircuit, QuantumRegister, ClassicalRegister

t = 4 
n = 4 
m = 7

qr=QuantumRegister(t,name="t")
ar=QuantumRegister(4,name="qr_U") # aquí 1 es la dimensión del espacio en el que opera U
cr=ClassicalRegister(t)

qc = QuantumCircuit(qr,ar,cr)   

qc.x(ar[0]) #  inicializamos la ancilla al autoestado de P(phi) ->  |u> = |1>
#qpe.h(ar[0]) #  

qc.h(range(n))
qc.barrier()

# aplicamos los operadores controlados c-U^j 
for q in range(t):
    qc.append(c_amod15(m, 2**q), [qr[q]] + ar[:])


qc.barrier()

# aplicamos la QFT^-1 que está definida en macro.py 
qc.append(TFC_adj(t),qr)

qc.measure(qr,cr)

qc.draw(output="mpl")

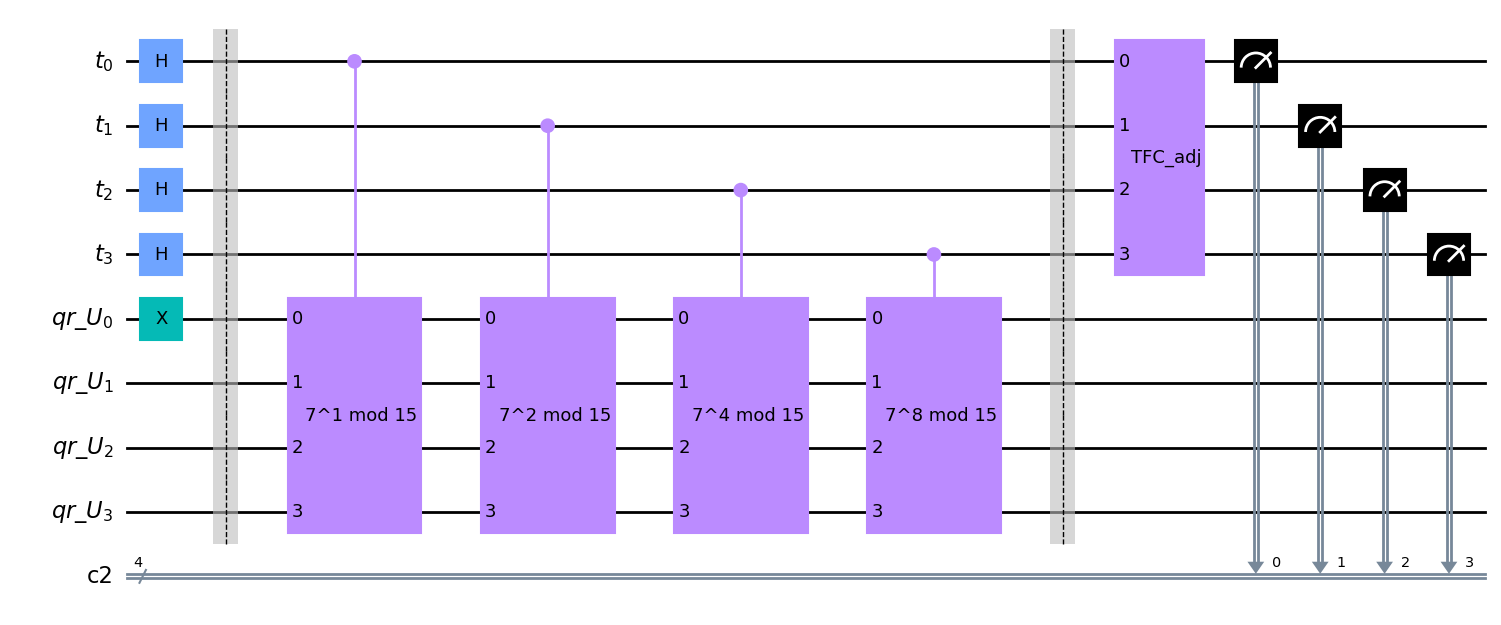
Ejecutamos el circuito y listamos los suceso más probables

'ejecutamos el circuito'
from qiskit.primitives import Sampler
from qiskit.visualization import plot_histogram, plot_bloch_multivector

nshots = 1000
dist = Sampler().run(qc,shots=nshots).result().quasi_dists[0]
counts = tQ.dist2counts(dist,t,nshots)

plot_histogram(counts)

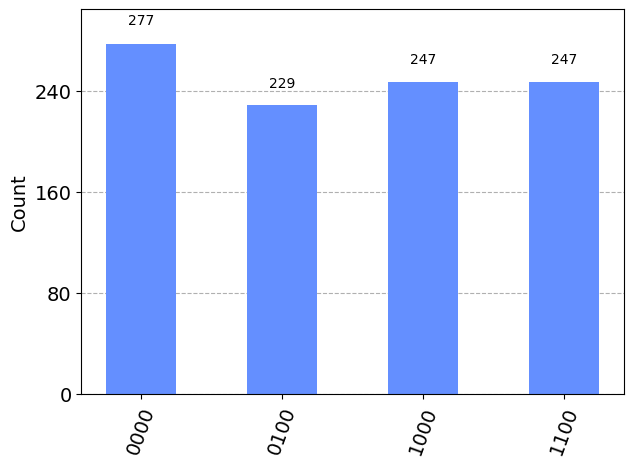
de aquí obtenemos la lista de valores enteros \(2^t s/r\)

Ns_list = sorted([int(keys,2) for  keys in counts])[1:] 
print('[2^ts/r] ~ ', Ns_list)

# dividiendo por 2**t
phis_list = [Ns_list[i]/2**t for i in range(len(Ns_list))]
print('phi_s', phis_list)

[2^ts/r] ~  [4, 8, 12]
phi_s [0.25, 0.5, 0.75]

Ahora podemos usar, como antes, dos estrategias para extraer el valor del período \(r\):

1. analizando las diferencias: \(r = \displaystyle \left(\frac{s+1}{r} - \frac{s}{r}\right)^{-1}\)

differences = [int((phis_list[s+1]-phis_list[s])**(-1)) for s in range(len(phis_list)-1)]

print(differences)

print('el valor entero del promedio =', int(sum(differences)/len(differences)))

[4, 4]
el valor entero del promedio = 4

2. usando la representación en fracciones continuas: \(\, \displaystyle \varphi_s = \frac{s}{r}\)

from fractions import Fraction
print('[s/r]=',[Fraction(phis_list[i]).limit_denominator(20) for i in range(int(len(phis_list)))])

[s/r]= [Fraction(1, 4), Fraction(1, 2), Fraction(3, 4)]

Notar

• En el caso más general \(\varphi_s = 2^t s/r \notin {\mathbb Z}\) no será un entero

• Entonces el resultado de la medida \(m_s\) seguirá una distribución de probabilidad picada en torno a la parte entera \(a_s = [2^t s/r]\)

• Haciendo un número alto de medidas y seleccionando los eventos \(m_s = a_s\) más probables podemos recuperar \(r\) por los mismos métodos anteriores.