Teoría de probabilidades para todas las edades

Teoría de probabilidades para todas las edades#

$ \newcommand{\bra}[1]{\langle #1|} $ $ \newcommand{\ket}[1]{|#1\rangle} $ $ \newcommand{\braket}[2]{\langle #1|#2\rangle} $ $ \newcommand{\i}{{\color{blue} i}} $ $ \newcommand{\Hil}{{\mathbb H}} $

Variables aleatorias#

Denotamos con $(X,p(X))$ una variable aleatoria donde

$X$ es el espacio muestral de valores $\{x_1, x_2,....,x_n\}$ que pueden aparecer en una consulta, o tirada
$p(X)$ es la distribución de probabilidad.

Distribución de probabilidad#

Una distribución de probabilidad es una función $x\to p(x)$ de los elementos del espacio muestral real $x\in X$ en los números reales $p(x)\in \mathbb{R}$. La probabilidad de un suceso imposible es $p(x) = 0$, y la de un suceso seguro es $p(x) = 1$.

La función $p(x)$ que debe verificar las dos condiciones siguientes para ser una distribución de probabilidad

\[ p(x) \in [0,1]~~~~~~~,~~~~~~~~\sum_{x\in X }p(x) = 1 \]

Es decir, la suma de probabilidades de todos los sucesos posibles debe ser la unidad, porque es la probabilidad de obtener algún miembro del espacio muestral.

Definición:

Media: la media de una variable aleatoria viene dada por la expresión

\[ \overline X = \sum_i x_i p(x_i) \]

Varianza: la varianza, $\sigma_X^2$, es la media de la desviación cuadrática $\overline{(x_i - \overline{X} )^2}$

\[ \sigma^2_X = \sum_j (x_j-\overline{X})^2 p(x_j) = \overline{X^2} - \overline{X}^2 \]

La cantidad $\sigma_X$ se denomina desviación estándar

\[ \sigma_X = \sqrt{\overline{X^2} - \overline{X}^2} \]

def random_prob_dist(n):
    p = np.random.rand(n)
    p /= np.sum(p)
    return p

random_prob_dist(10)

array([0.06550321, 0.00045257, 0.22756174, 0.07922132, 0.19390968,
       0.03356594, 0.16785773, 0.08862708, 0.10628265, 0.03701809])

La conexión estadística#

Nuestro conocimiento del mundo se basa en la realización de experimentos, el resultado de los cuales es (empíricamente) aleatorio.

Podemos pensar en el hecho de medir un sistema como la consulta de una variable aleatoria $(X,p(X))$ donde la distribución de probabilidad incorpora todo nuestro conocimiento acerca del sistema

Frecuencias e Histogramas#

Cualquier consulta o medida da lugar a una muestra finita de valores $A_N = (a_1,a_2,...,a_N)$ donde $a_i\in \{x_1,...,x_n\}$ pueden repetirse en la muestra, con números de aparición $n(x_i)$ tales que $n(x_1) + \ldots + n(x_p) = N$.

Estos datos se pueden agrupar en intervalos o bins que eliminen cierta precisión numérica.

Por ejemplo, si truncamos nuestra precisión a las décimas de unidad, $13.10$ y $13.19$ pertenecerán al mismo bin.

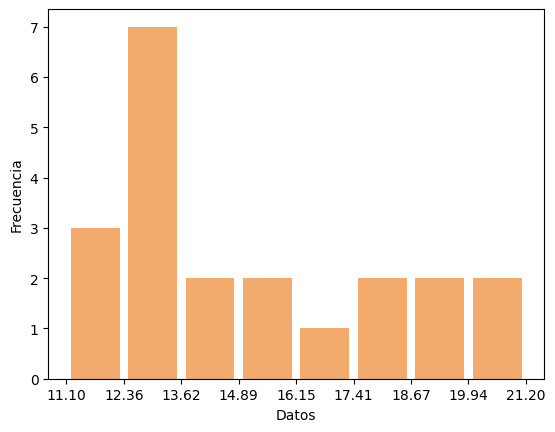
Un histograma es un diagrama en el que, por cada bin, hay una columna, cuya altura representa el número de sucesos que pertenecen a dicho bin

En el siguiente ejemplo, puedes ver cómo, la misma lista de datos conduce a distintos histogramas si cambias la anchura de los bins

import numpy as np
import matplotlib.pyplot as plt

datos1 = [12.2, 15.3, 13, 12.8, 18.1, 13, 20, 19.5, 20.2, 12.1, 12.4, 13.2, 17.9, 14.1, 15, 13.4, 11.1, 14.6, 13, 17.4, 19.2]
datos2 = np.linspace(0.,10.,200)
datos  = datos1

anchura_bins = 1.# para modificar la anchura de los bins
num_bins = int((max(datos)-min(datos))/anchura_bins) #número de bins
bins_list = np.linspace(min(datos), max(datos) + 1 ,num_bins) #calculamos los extremos de los intervalos


counts, bins, ignore = plt.hist(x=datos, bins = bins_list, color='#F2AB6D', rwidth=0.85)
plt.xlabel('Datos')
plt.ylabel('Frecuencia')
plt.xticks(bins_list)

plt.show()

../../../_images/a12b2646afab44fd2eba62ab7fc01b36580e34035f972cf7bdfc083f6243dae5.png

Ley de los grandes números#

Las fracciones relativas tienden en el límite $N\to \infty$ a la probabilidad relativa de aparición de $x_i$ en una sola tirada

\[ f_N(x_i) = \frac{n(x_i)}{N}~~~\stackrel{N\to\infty}{\longrightarrow}~~~{p(x_i)} \]

Experimentalmente sólo tenemos acceso a las frecuencias relativas $f_N(x_i)$ para un $N$ grande aunque finito.

Igualmente, nuestro conocimiento de la media $\overline X$ y la varianza $\sigma_X^2$ siempre es aproximado, y se realiza a través de las medias y varianzas muestrales

\[\begin{split} \begin{eqnarray*} \overline{A}_N = \sum_i x_i f_N(x_i)~~~&\stackrel{N\to\infty}{\longrightarrow}&~~~ \overline{X}\\ \sigma_{A_N}^2 = \sum_{i} (x_i - \overline{A}_N)^2 f_N(x_i) ~~~&\stackrel{N\to\infty}{\longrightarrow}&~~~ \sigma_X^2 \end{eqnarray*} \end{split}\]

Distribuciones frecuentes#

La distribución de Bernouilli#

Una variable aleatoria de Bernouilli $X=(x,p(x))$ tiene dos posibles resultados

éxito $\to x=1$ con probabilidad $p(1) = p$
fracaso $\to x=0$ con probabilidad $p(0) = 1-p$

Podemos calcular fácilmente

\[\begin{split} \begin{eqnarray} \overline X &=& \sum_i x_i p_i =1 \cdot p + 0\cdot (1-p) = p\\ \sigma^2 &=& \sum_i (x-\overline X )^2p_i = (1-p)^2 p +(0-p)^2(1-p) = p(1-p) \end{eqnarray} \end{split}\]

Distribución binomial#

La variable aleatoria binomial $X = (x,p(x))$ se define como

\[ x = \hbox{número de $éxitos$ obtenidos en $n$ pruebas de Bernouilli sucesivas } \]

Claramente $x \in (0,1,2,...n)$.

Ahora es muy sencillo obtener la probabilidad de un suceso con $x$ éxitos

\[\begin{split} p(x) = \begin{pmatrix}n\\ x\end{pmatrix} p^x (1-p)^{n-x} \end{split}\]

donde el primer factor tiene en cuenta las posibles ordenaciones en que aparecen $x$ éxitos en $n$ intentos.

Un cálculo un poco más largo permite ver que, ahora

(12)#\[\begin{eqnarray} \overline X &=& np\\ \rule{0mm}{7mm} \sigma^2 &=& n p(1-p) \end{eqnarray}\]

La distribución normal#

Vamos a estudiar la distribución normal centrada en $\mu$ y con anchura $\sigma$

\[ p(x) = \frac{1}{\sqrt{2\pi}\sigma} \exp \left({-\frac{(x-\mu)^2}{2\sigma^2}}\right) \]

Nos encontramos ante una variable aleatoria con un espacio muestral continuo $x\in (-\infty,+\infty)$.

(13)#\[\begin{eqnarray} \overline{X} &=& \int_{-\infty}^{+\infty} xp(x) dx = \mu \\ \overline{(x-\overline X)^2} &=& \int_{-\infty}^{+\infty} (x-\mu)^2 p(x)dx =\sigma^2 \end{eqnarray}\]

'generamos una instancia de la distribución normal'
mu, sigma = 0, 0.1 
N = 10000
s = np.random.normal(mu, sigma, N)

import matplotlib.pyplot as plt


'generamos una instancia de histograma con un número de bins'
num_bins=100
counts, bins, ignore = plt.hist(s, num_bins, density=True)
'extraemos los bins para hacer el plot de la funcion analítica'


'dibujamos la función analítica para comparar'
def gaussian(x,mu,sigma):
    return 1/(sigma * np.sqrt(2 * np.pi))*np.exp( - (x - mu)**2 / (2 * sigma**2) )
    
plt.plot(bins, gaussian(bins,mu,sigma),linewidth=2, color='r')

plt.show()

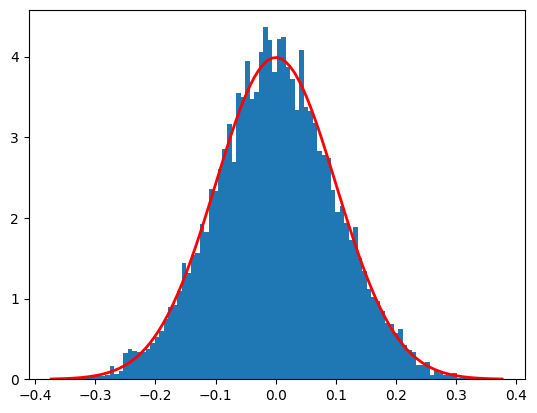
../../../_images/6f42f8bea05dbb2921b48667fac4626a630e684d6280ea3352af64be700090ac.png

En el límite de número de eventos $N\to \infty$, el histograma y la curva matemática confluyen.

Probabilidades combinadas#

Las probabilidades combinadas son la base de las correlaciones. Es aquí donde la Mecánica Cuántica predice resultados diferentes a la Mecánica Clásica.

Ahora vamos a examinar variables aleatorias formadas por dos espacios muestrales $X$ e $Y$. Dependiendo de la forma en que combinemos la observación de cada una tendremos distintas distribuciones de probabilidad

Probabilidad combinada#

La probabilidad combinada $p(X,Y)$ asocia un número $p(x,y)$ a la probabilidad de observación conjunta de $x$ e $y$.

Hay que tratar las parejas de eventos como un solo evento $a = (x,y)$. Por eso, la condición de normalización ahora es

\[ \sum_a p(a) = \sum_{xy} p(x,y) = 1\, . \]

La suma parcial sobre una de las dos variables conduce a sendas distribuciones marginales

\[ q(x) = \sum_{y} p(x,y) ~~~~~~~~~ \tilde q(y) = \sum_{x} p(x,y) \]

Si la probabilidad combinada es el producto de las probabilidades de los miembros del par, decimos que $X$ e $Y$ son variables aleatorias independientes

\[ p(x,y) = p(x) p(y) \]

La distribución de cada variable coincide con la que se deduce de marginalizar la otra

\[ \sum_y p(x,y) = p(x)~~~~,~~~~\sum_x p(x,y) = p(y) \]

Probabilidad condicionada#

La distribución de probabilidad condicionada $p(X|Y)$ asigna un número $p(x|y)$ a la probabilidad de encontrar un suceso $X=x$ una vez sabemos que $Y=y$ ha sido el resultado de consultar $Y$.

La manera de acceder experimentalmente a estas distribuciones, es efectuar un muestreo $(a_i,b_i)$, $i=1,...,N$ de valores de $(X,Y)$ y seleccionar sólo aquellos sucesos donde $b_i = y$ un valor concreto de $Y$.

Teorema de Bayes#

Las probabilidades condicionales y combinadas no son independientes. Se relacionan de la forma siguiente

\[ p(x,y) = p(x|y)p(y) = p(y|x) p(x)= p(y,x) \]

La segunda igualdad conduce al teorema de Bayes

Teorema: de Bayes

\[ p(x|y) = p(y|x) \frac{p(x)}{p(y)} \]