May 15, 2024 | 7 min read

El arte de medir I

\( \newcommand{\bra}[1]{\langle #1|} \) \( \newcommand{\ket}[1]{|#1\rangle} \) \( \newcommand{\braket}[2]{\langle #1|#2\rangle} \) \( \newcommand{\i}{{\color{blue} i}} \) \( \newcommand{\tr}{{\rm tr}} \) \( \newcommand{\Hil}{{\mathcal H}} \) \( \newcommand{\boldn}{{\bf n}} \) \( \newcommand{\bn}{{\bf n}} \) \( \newcommand{\boldsig}{\boldsymbol{\sigma}} \) \( \newcommand{\bsig}{\boldsymbol{\sigma}} \)

Show code cell source Hide code cell source

%run ../../macro_tQ.py
import sys
sys.path.append('../../')
import macro_tQ as tQ

import numpy as np
from IPython.display import display,Markdown,Latex
from qiskit.visualization import array_to_latex

Medidas de 1 cúbit

Medidas en la base computacional

El circuito de medida estándar se representa en la forma siguiente

Por defecto, se trata de una medida proyectiva asociada al operador observable \(Z\). Es decir, proyecta a la base \(\ket{a} = \ket{0},\ket{1}\) de autoestados de \(Z\)

\[ Z\ket{0} = +\ket{0}~~~~,~~~~~ Z\ket{1} = -\ket{1} \]

Podemos abreviar de forma conjunta, con \(~a=0,1\)

\[ Z\ket{a} = (-1)^a\ket{a} \]

Probabilidades de medida

Una repetición de medidas del estado \(\ket{\psi} = c_0\ket{0} + c_1\ket{1}\) da acceso estadístico a las amplitudes de probabilidad

\[ p(0) = \frac{n_{0}}{N} = |c_0|^2 = |\braket{0}{\psi}|^2~~~~~~~~~~~~~~~~ p(1) = \frac{n_{1}}{N}=|c_1|^2 = |\braket{1}{\psi}|^2 \, . \]

Este procedimiento de reconstrucción es la base de la tomografía cuántica.

Definamos un vector aleatorio

from qiskit.quantum_info import Statevector
from qiskit.visualization import plot_bloch_multivector, array_to_latex  

theta = 1.9
phi   = 0.8

psi_ket = np.array([np.cos(theta/2),(np.exp(1j*phi))*np.sin(theta/2)]).reshape(2,1)
array_to_latex(psi_ket,prefix= '\ket{\psi} = ')

display(Statevector(psi_ket).draw('latex'))
display(Statevector(psi_ket).draw('Bloch'))

\[0.5816830895 |0\rangle+(0.5667120397 + 0.5835085668 i) |1\rangle\]

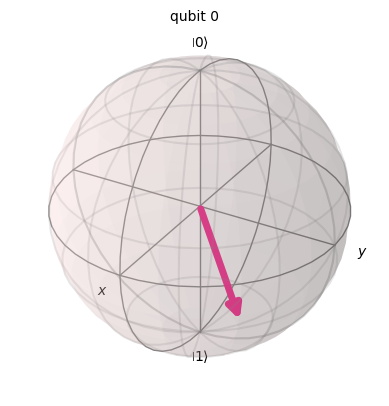
Las probabilidades de obtener ‘0’ y ‘1’ son los cuadrados de las amplitudes en valor absoluto

p0 = np.abs(psi_ket[0])**2
p1 = np.abs(psi_ket[1])**2

print('p(0)=', np.round(p0,5),', p(1)=', np.round(p1,5))

p(0)= [0.33836] , p(1)= [0.66164]

Vamos a recuperarlas experimentalmente corriendo un circuito. Primero obtenemos el diccionario de cuentas obtenidas después de ejecutar el circuito un número de veces

nshots = 10000

Qibo

from qibo.models.circuit import Circuit, gates

'generamos un circuito en el que inicializamos el estado psi'
qc_psi_Qibo = Circuit(1)
qc_psi_Qibo.add(gates.U3(0, theta, phi, 0, trainable=True))
qc_psi_Qibo.add(gates.M(0))
display(tQ.draw_qibo_circuit_mpl(qc_psi_Qibo))
'ejecutamos un número de veces'
counts_psi = qc_psi_Qibo(nshots=nshots).frequencies()

'visualizamos los resultados como un diccionario y  mediante un histograma'
from qiskit.visualization import plot_histogram
print('counts_psi = ',counts_psi)
plot_histogram(counts_psi) # Mostramos un histograma de resultados

Qiskit

from qiskit import QuantumCircuit
from qiskit_aer import AerSimulator

'generamos un circuito en el que inicializamos el estado psi'
qc_psi_Qiskit = QuantumCircuit(1,1)
qc_psi_Qiskit.u(theta,phi,0,0)
qc_psi_Qiskit.measure(0,0)
display(qc_psi_Qiskit.draw('mpl'))

'ejecutamos un número de veces'
counts_psi = AerSimulator().run(qc_psi_Qiskit,shots=nshots).result().get_counts()

'visualizamos los resultados como un diccionario y  mediante un histograma'
from qiskit.visualization import plot_histogram
print('counts_psi = ',counts_psi)
plot_histogram(counts_psi) # Mostramos un histograma de resultados

/opt/anaconda3/envs/TalentQ/lib/python3.11/site-packages/qiskit/visualization/circuit/matplotlib.py:266: FutureWarning: The default matplotlib drawer scheme will be changed to "iqp" in a following release. To silence this warning, specify the current default explicitly as style="clifford", or the new default as style="iqp".
  self._style, def_font_ratio = load_style(self._style)

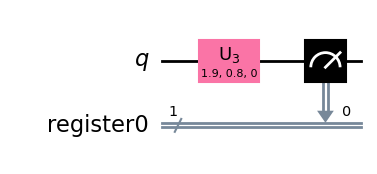
[Qibo 0.1.12.dev0|INFO|2024-03-11 21:40:15]: Using tensorflow backend on /device:CPU:0

counts_psi =  Counter({'1': <tf.Tensor: shape=(), dtype=int64, numpy=6618>, '0': <tf.Tensor: shape=(), dtype=int64, numpy=3382>})

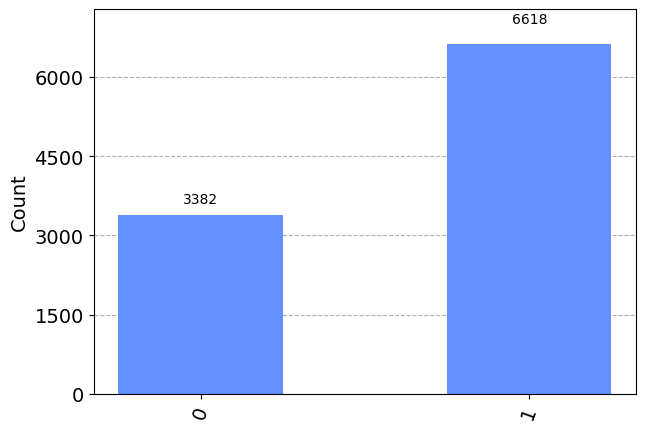
Ahora podemos calcular las frecuencias relativas \(n_i/N\) y compararlas con las probabilidades \(p(i)\)

p0_experiment = counts_psi['0']/nshots
p1_experiment = counts_psi['1']/nshots

print('p(0)_experiment =', p0_experiment,'  p(1)_experiment = ',p1_experiment)

p(0)_experiment = tf.Tensor(0.3382, shape=(), dtype=float64)   p(1)_experiment =  tf.Tensor(0.6618, shape=(), dtype=float64)

Interferencia cuántica y medidas

El resultado de tirar una moneda al aire es una variable aleatoria binaria equiprobable: X = (cara,cruz). Es irrelevante si analizamos el resultado cada tirada o cada dos, o tres tiradas. Las frecuencias relativas de caras y cruces, siempre serán próximas a \(1/2\).

Podemos imaginar un experimento similar con un cúbit, donde cara \(\to \ket{0}\) y cruz \(\to\ket{1}\) son los estados posibles de la medida en la base \(Z\)

• tirar la moneda clásica es ponerla en un estado incierto que puede acabar en cara o cruz al caer sobre la mesa (medir)

• tirar la moneda cuántica es aplicar el operador \(H\) para poner cualquiera de los dos resultados en una superposición \(H\ket{0} = \frac{1}{\sqrt{2}}(\ket{0} + \ket{1})\) y \(H\ket{1} = \frac{1}{\sqrt{2}}(\ket{0} - \ket{1})\)

El resultado clásico y cuántico, para una sola tirada, coinciden en una distribución equiprobable

\[ \ket{0}~ \stackrel{\rm tirar}{\longrightarrow} ~ H \ket{0}= \ket{+} ~ \stackrel{\rm medir}{\longrightarrow} ~p(0) = p(1) = 0.5 \]

La sorpresa está en observar el resultado ¡después de dos tiradas! Para una moneda clásica, la distribución volvería a ser equiprobable.

\[ \ket{0}~ \stackrel{\rm tirar}{\longrightarrow} ~ H \ket{0}~ \stackrel{\rm tirar}{\longrightarrow} H^2\ket{0} = \ket{0} ~ \stackrel{\rm medir}{\longrightarrow} ~p(0) = 1 ~,~p(1) = 0 \]

Cuánticamente observamos que se recupera el estado inicial, cara, ¡con un 100% de probabilidad!

Es interesante ver este caso como ejemplo de interferencia cuántica, una herramienta que explotaremos intensivamente para fabricar algoritmos. En efecto el proceso de hacer dos tiradas sucesivas (sin medir entre ellas) genera la siguiente sucesión estados

\[\begin{split} \begin{array}{rcl} \ket{0} &\stackrel{H}{\to}& \frac{1}{\sqrt{2}}(\ket{0} + \ket{1}) \\ \rule{0mm}{8mm} &\stackrel{H}{\to}& \frac{1}{2}(\ket{0} + \ket{1}) + \frac{1}{2}(\ket{0} - \ket{1}) \\ \rule{0mm}{8mm} &=& \frac{1}{2}(\ket{0} + \ket{0}) + \frac{1}{2}(\ket{1} - \ket{1}) \rule{0mm}{8mm}\\ \rule{0mm}{8mm}& =& \ket{0} \end{array} \end{split}\]

El resultado final es cierto y arrojará \(0\) con 100% de probabilidad. Vemos que hay dos caminos posible para alcanzar cualquier resultado final, \(\ket{0}\) ó \(\ket{1}\). Los que intervienen para conseguir \(\ket{0} \to \ket{0}\) contribuyen de manera constructiva, mientras que los dos caminos \(\ket{0}\to \ket{1}\) interfieren de forma destructiva. El signo menos en el segundo estado \(\ket{1}\) es una amplitud de probabilidad negativa, algo imposible clásicamente.

Ejercicio

repite el razonamiento anterior

• comenzando con el estado cruz, es decir \(\ket{1}\)

• intercalando una medida entre ambas tiradas

El resultado del ejercicio anterior ilustra que la introducción de una medida intermedia destruye la interferencia. La interferencia es una propiedad ligada a la coherencia cuántica, la cual se pierde través de la interacción del cúbit con el ambiente. Las medidas son interacciones de ese tipo.

Ejercicio

construye un circuito y verifica los resultados que predice la mecánica cuántica. Estudia la introducción de más tiradas cuántica, \(H^n\). Intercala una medida en distintas partes del circuito y mira qué resultado obtienes.

Medidas en bases generales

La elección del observable \(Z\) para el medidor en la base computacional es arbitrario. Deberíamos ser capaces de modificar la base de medida a voluntad. Vamos a estudiar primero cómo usar las bases \(X\) e \(Y\) y después analizaremos el caso arbitrario.

Bases X e Y

Los autovectores del operador \(X\) se denominan convencionalmente \(\ket{+}, \ket{-}\). Desearíamos disponer de un circuito asociado a este observable, de forma que, a la detección de un autovector \(\ket{+} \) registrase un \(0\) y de \(\ket{-} \) un \(1\).

Es fácil construir un circuito así, como se ve en la figura a continuación. Efectivamente la acción de \(H\ket{+} = \ket{0}\) y \(H\ket{-} = \ket{1}\) manda cada autoestado de \(X\) a un autoestado de \(Z\). A continuación un medidor estándar registrará el valor de \(a =0,1\) según sea el estado medido. Una aplicación posterior de \(H\) nos devolverá el estado original \(H\ket{0} = H^2 \ket{+} = \ket{+}\) e igualmente \(H\ket{1} = H^2 \ket{-} = \ket{-}\)

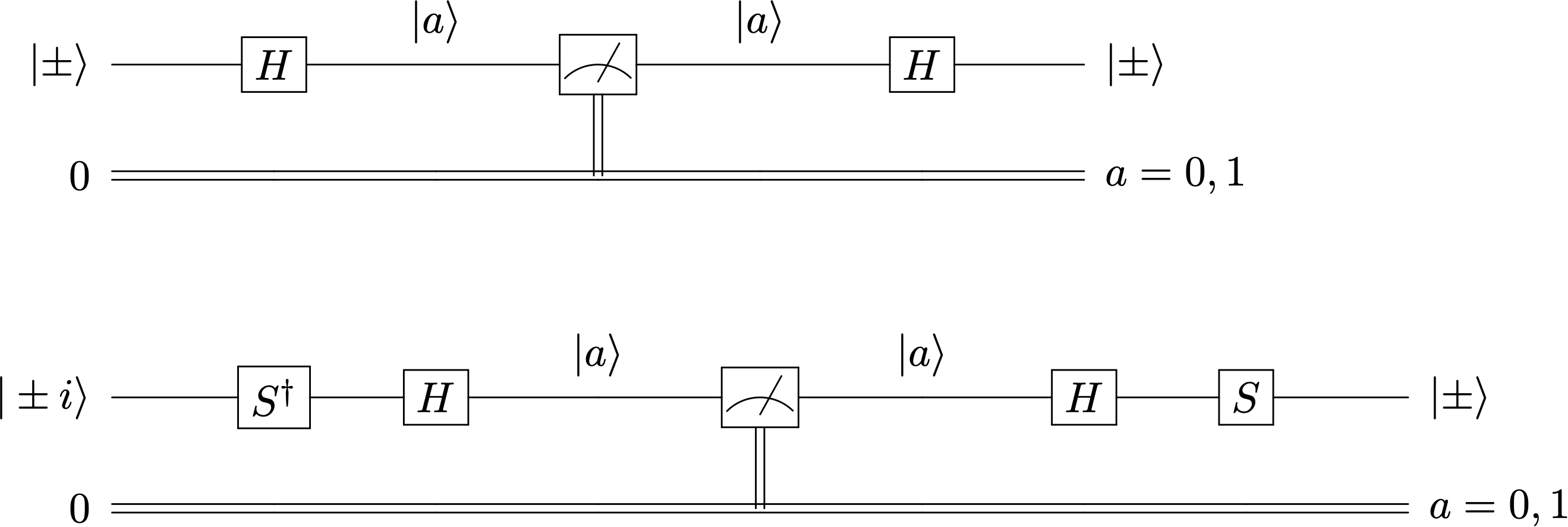
Igualmente denominemos \(\ket{+ i}\) y \(\ket{- i}\) los autoestados del operador \(Y\). Podemos construir un circuito que registra \(a = 0,1\) cuando el estado incidente colapsa a \(\ket{+ i}\) y \(\ket{- i}\) respectivamente. Basta observar que \(\ket{\pm i} = SH\ket{a}\). Inversamente \(\ket{a} = HS^\dagger \ket{\pm i}\) y proceder igual que antes.

En resumen: podemos construir aparatos de medida efectivos que actúan sobre las bases \(X\) e \(Y\) igual que el medidor estándar lo hace sobre \(Z\)

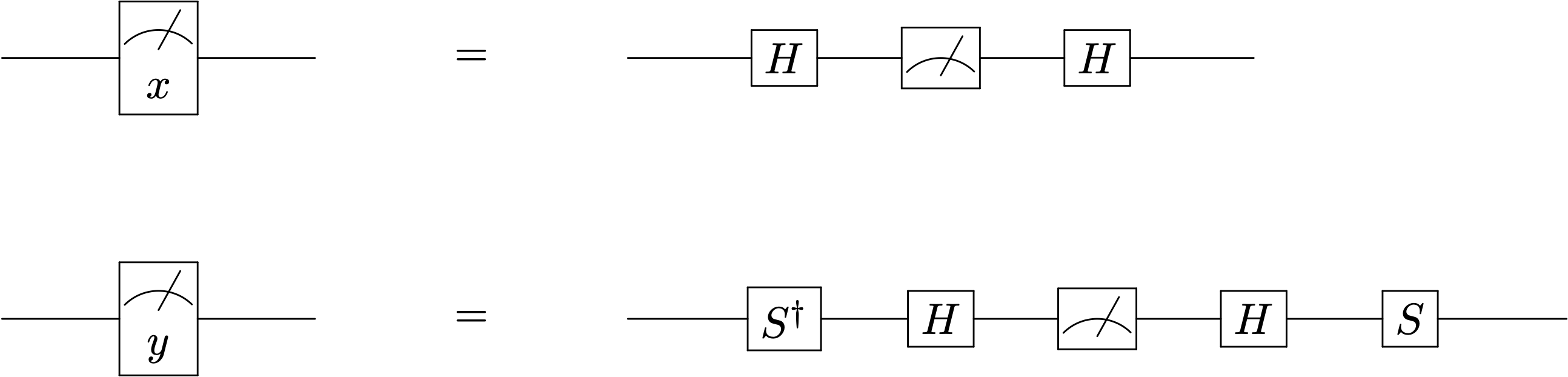
Detrás de estas equivalencias de circuitos, ahora con medidores, se esconde la conjugación de puertas siguiente

\[ X = H Z H ~~~~~~~~,~~~~~~~~~Y = SHZ HS^\dagger \]

Nota

recuerda que el orden de la composición de operadores se invierte al plasmarlos en un circuito

Ejercicio

Comprueba que estas ecuaciones de conjugación son correctas

Formalismo general

Vamos a ver los dos casos anteriores como caso particulares de un aparato de medida asociado a una dirección arbitraria en la esfera de Bloch. Dado un vector unitario \(~\hat\boldn~\)

\[ \hat\bn(\theta,\phi) = \sin\theta\cos\phi \, \hat {\bf x} + \sin\theta\sin\phi \, \hat {\bf y} + \cos\theta \, \hat {\bf z} \]

el observable asociado será \( \hat{\boldn}\cdot \boldsymbol{\sigma}\) cuyos autoestados forman una base \(\{\ket{0}_{\hat{\bf n}}, \ket{1}_{\hat{\bf n}}\}\) con autovalores \(\pm 1\)

\[ \hat{\boldn}\cdot \boldsymbol{\sigma}\,\ket{0}_{\hat{\bf n}} = + \ket{0}_{\hat{\bf n}}~~~~~~,~~~~~~~ \hat{\boldn}\cdot \boldsymbol{\sigma}\,\ket{1}_{\hat{\bf n}} = - \ket{1}_{\hat{\bf n}} \]

dados por

\[\begin{split} \ket{0}_{\hat{\bf n}} = ~\begin{bmatrix} \cos\displaystyle\frac{\theta}{2} \\ ~e^{i\phi}\sin\displaystyle\frac{\theta}{2} \end{bmatrix} ~~~~~~~~~~~,~~~~~~~~~~~ \ket{1}_{\hat{\bf n}} = \begin{bmatrix} -e^{-i\phi}\sin\displaystyle\frac{\theta}{2} \\ \cos\displaystyle\frac{\theta}{2} \end{bmatrix} \end{split}\]

Los casos particulares de la sección anterior se recuperan haciendo

\[\begin{split} \begin{array}{ccl} Z = \hat{\bf z} \cdot \boldsymbol{\sigma} ~~&\rightarrow& ~~\{\ket{0},\ket{1} \} = \{\ket{0}_{\hat{\bf z}},\ket{1}_{\hat{\bf z}}\}\\ \rule{0mm}{8mm} X = \hat{\bf x} \cdot \boldsymbol{\sigma} ~~&\rightarrow& \{\ket{+},\ket{-}\} = \{\ket{0}_{\hat{\bf x}},\ket{1}_{\hat{\bf x}}\} \\ \rule{0mm}{8mm} Y = \hat{\bf y} \cdot \boldsymbol{\sigma} ~~&\rightarrow& \{\ket{+i},\ket{-i}\} = \{\ket{0}_{\hat{\bf y}},\ket{1}_{\hat{\bf y}}\} \end{array} \end{split}\]

Usando operadores de rotación podemos convertir el medidor estándar asociado a \(Z\) con un medidor efectivo asociado al observable general \(\hat {\bf n} \cdot \bsig\). Veamos cómo:

• sea \(~\hat{\bf z}\cdot\bsig ~\) el aparato de medida estandar orientado a lo largo del eje \(~\hat{\bf z}\)

\[ \hat{\bf z}\cdot \bsig \, \ket{a}_{\hat{\bf z}} = (-1)^a\ket{a}_{\hat{\bf z}} = Z \ket{a} \]

• y \(~\hat\bn\cdot \bsig~\) el aparato de medida orientado a lo largo del eje \(\hat\bn\)

\[ \hat\bn\cdot \bsig \, \ket{a}_{\hat{\bf n}} = (-1)^a\ket{a}_{\hat{\bf n}} \]

las bases de autovectores asociadas \(\{\ket{a}_{\hat{\bf z}}\}\) y \(\{\ket{a}_{\hat{\bf n}}\}\) ser relacionan mediante una simple rotación unitaria

\[ \ket{0}_{\hat\boldn} = U \ket{0}_{\hat{\bf z}}~~~~~~,~~~~~~ \ket{1}_{\hat\boldn} = U \ket{1}_{\hat{\bf z}} \]

El operador en cuestión es

\[\begin{split} U(\hat {\bf z}\to \hat \bn) = U(\theta,\phi,0)=\begin{bmatrix} \cos \displaystyle\frac{\theta}{2} & - \sin\displaystyle\frac{\theta}{2} \\ \rule{0mm}{4mm} e^{i\phi} \sin \displaystyle\frac{\theta}{2} &e^{i\phi} \cos \displaystyle\frac{\theta}{2} \end{bmatrix} \end{split}\]

como es fácil de comprobar

\[\begin{split} \begin{bmatrix} \cos\theta \\ e^{i\phi}\sin\theta \end{bmatrix} = U\cdot \begin{bmatrix}1\\0 \end{bmatrix} ~~~~~~~,~~~~~~~ \begin{bmatrix} -\sin\theta \\ e^{i\phi}\cos\theta \end{bmatrix} = U\cdot \begin{bmatrix}0\\1 \end{bmatrix} \end{split}\]

Si las componentes de los vectores rotan en la forma \(\ket{a}_{\hat{\bf n}} = U\ket{a}_{\hat{\bf z}}\) los observables asociados se relacionan algebraicamente como lo hace cualquier operador

\[ \hat {\bf n} \cdot\bsig = U \, (\hat {\bf z} \cdot \bsig)\, U^\dagger \]

Verificamos la consistencia

(16)\[\begin{eqnarray} \hat {\bf n} \cdot \bsig\, \ket{a}_{\hat{\bf n}} ~~&=&~~ U~ \hat {\bf z} \cdot \bsig ~ U^\dagger ~ U \ket{a}_{\hat{\bf z}}\\ \rule{0mm}{8mm} &=& U~ \hat {\bf z} \cdot \bsig ~ \ket{a}_{\hat{\bf z}}\\ \rule{0mm}{8mm} &=& U\, Z \ket{a} = U (-1)^a \ket{a}_{\hat{\bf z}} \\ \rule{0mm}{8mm} &=& (-1)^a U\ket{a}_{\hat{\bf z}} \\ \rule{0mm}{8mm} &=& (-1)^a \ket{a}_{\hat{\bf n}} \rule{0mm}{8mm} \end{eqnarray}\]

Ejercicio

comprueba operando la ecuación anterior

El circuito siguiente simula un aparato de medición en la base \(\{\ket{a}_{\hat{\bf n}}\}\) obtenido mediante la rotación del aparato de medida en la base \(\{\ket{a}_{\hat{\bf n}}\}\) de autoestados de \(Z\)

Notar que

• los casos particulares de bases \(X\) e \(Y\) se recuperan con \(U = H\) en el primer caso y \(U = SH\) en el segundo.

• si el estado se destruye en la medida o no es conservado posteriormente, podemos simplificar el circuito de medida para que sólo informe del valor medido

Valores esperados de un observable

Conociento la probabilidades de aparición de los posible autovalores \(\lambda_i\) de un operador \(A\) tenemos acceso al valor esperado

\[ \langle A \rangle_\psi = \bra{\psi}A\ket{\psi} = \sum_i p(\lambda_i) \lambda_i \]

Como sólo disponemos de un observable, el medidor estándar en la dirección \(Z\), tendremos que ser creativos para poder obtener este valor esperado. La clave está en que sólo necesitaremos los medidores efectivos en las bases \(X, Y \) y \(Z\).

Descomposición en la base de Pauli

La clave reside en observar que cualquier observable sobre un cúbit \(A = A^\dagger\) puede desarrollarse en la base \(\sigma_i = \{I,X,Y,Z\}, \, i=0,1,2,3\)

\[ A = a_0 I + a_1 X + a_2 Y + a_3 Z \, . \]

con coeficientes

\[ a_i = \frac{1}{2} \tr \, (A \sigma_i)\, . \]

Esta expresión se obtiene haciendo uso de la relación \(\to \frac{1}{2} \tr\, (\sigma_i \sigma_j) = \delta_{ij}\).

Comprobación

\[ \frac{1}{2} \tr \, (A \sigma_i) = \frac{1}{2} \tr \, \left((\sum_{j=0}^3 a_j \sigma_j) \sigma_i\right) = \sum_{j=0}^3 a_j \, \frac{1}{2} \tr ( \sigma_j \sigma_i) = \sum_{j=0}^3 a_j \delta_{ji} = a_i \]

Entonces, podremos obtener el valor esperado de \(A\) si somos capaces de medir los de \(X,\) \(Y\) y \(Z\).

\[\begin{eqnarray*} \langle A\rangle_\psi ~=~\bra{\psi}A\ket{\psi} ~&=& ~ \bra{\psi} a_0 I + a_1 X + a_2 Y + a_3 Z \ket{\psi} \\ \rule{0mm}{8mm} &=& ~a_0 + a_1 \langle X\rangle_\psi + a_2 \langle Y\rangle_\psi + a_3 \langle Z\rangle_\psi \end{eqnarray*}\]

• \(\langle Z \rangle_{\psi}\)

Los estados de la base computacional son autoestados del operador \(Z\) con autovalor \(\pm 1\)

\[ Z \ket{0} =+ \ket{0} ~~~~~~~~~~~~~~~~~~~~~ Z \ket{1} =-\ket{1} \]

Dado un estado \(\ket{\psi} = c^Z_0\ket{0} + c^Z_1\ket{1}\), la medida repetida arroja de forma aleatoria los valores propios de \(Z \to \pm 1\) con frecuencias relativas

\[(+1)\to n^Z_0 ~~~~~~~~~~~~~~~~~~~~~~~~ (-1)\to n^Z_1\]

El valor medio de dicha variable es,

\[\begin{eqnarray*} \langle Z \rangle_\psi = \bra{\psi} Z \ket{\psi} &=& \left( c^Z_0\bra{0} + c^Z_1\bra{1}\right) Z\left( c^Z_0\ket{0} + c^Z_1\ket{1}\right) \nonumber \\ \rule{0mm}{10mm} &=& (+1) |c^Z_0|^2 + (-1) |c^Z_1|^2 \nonumber \\ \rule{0mm}{10mm} &=& +\frac{n^Z_0}{N}- \frac{ n^Z_1}{N} \end{eqnarray*}\]

Para medir autovalores de \(\langle Z\rangle_\psi\) el circuito es el más simple

• \(\langle X \rangle_{\psi}\)

En la base \(X\), el mismo estado de entrada se escribirá con otras componentes \(\ket{\psi} = c_0^X\ket{+} + c_1^X\ket{-}\).

Si ahora medimos \(\ket{\psi}\) en la base \(X\), la repetición arrojará una muestra aleatoria de autovalores de \(X\to \pm 1\) con frecuencias

\[~(+1)\to n^X_0 ~~~~~~~~~~~~~~~~~~~ (-1)\to n^X_1 \]

El valor esperado de \(X\) se obtiene del promedio de frecuencias relativas

\[ \langle X \rangle_\psi ~= (+1)|c_0^X|^2 +(-1)|c_1^X|^2 ~=~ +\frac{n^X_0}{N}- \frac{ n^X_1}{N} \]

Ya hemos visto cuál es el circuito necesario para medir en la base \(X\)

• \(\langle Y \rangle_{\psi}\)

Igualmente, si medimos el estado \(\ket{\psi} = c_0^Y\ket{+i} + c_1^Y\ket{-i}\) con un medidor asociado al operador \(Y = SHZHS^\dagger\), la repetición arrojará una muestra aleatoria de valores propios de \(Y\to \pm 1\) con frecuencias relativas \(+1\to n^Y_0\) y \(-1\to n^Y_1\). Entonces

\[ \langle Y \rangle_\psi = +\frac{n^Y_0}{N}- \frac{ n^Y_1}{N}\, . \]

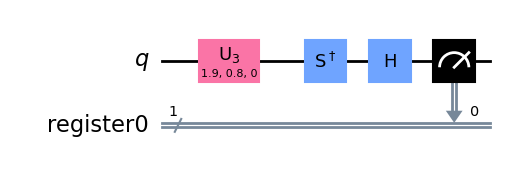
Circuito necesario para medir en la base \( Y\)

Qibo

from qibo.models.circuit import Circuit, gates

qc_psi_Qibo = Circuit(1)
qc_psi_Qibo.add(gates.U3(0, theta, phi, 0, trainable=True))

'añadimos el medidor efectivo segun queramos medir sea <X>, <Y> o <Z>'
P = 'Y'

if P =='X':
    qc_psi_Qibo.add(gates.h(0))    

elif P =='Y':
    qc_psi_Qibo.add(gates.SDG(0))    
    qc_psi_Qibo.add(gates.H(0))    

qc_psi_Qibo.add(gates.M(0))
display(tQ.draw_qibo_circuit_mpl(qc_psi_Qibo))

'ejecutamos'
nshots = 10000
counts_psi = qc_psi_Qibo(nshots=nshots).frequencies()
print(counts_psi)

'Ahora,con las frecuencias relativas de los autovalores  de Z, podemos calcular los valores medios'
mean_P = 0
for bits, counts  in counts_psi.items():
    mean_P += (-1)**(int(bits))* (counts/nshots)

print('<',P,'>','=',np.round(mean_P,5))

Qiskit

qc_psi_Qiskit = QuantumCircuit(1,1)
qc_psi_Qiskit.u(theta,phi,0,0)

'añadimos el medidor efectivo segun queramos medir sea <X>, <Y> o <Z>'
P = 'Y'

if P =='X':
    qc_psi_Qiskit.h(0)    

elif P =='Y':
    qc_psi_Qiskit.sdg(0)
    qc_psi_Qiskit.h(0)

qc_psi_Qiskit.measure(0,0)    
display(qc_psi_Qiskit.draw('mpl')) 

nshots = 100000
from qiskit_aer import AerSimulator

counts_psi = AerSimulator().run(qc_psi_Qiskit,shots = nshots).result().get_counts()
print(counts_psi)


'Ahora,con las frecuencias relativas de los autovalores  de Z, podemos calcular los valores medios'
mean_P = 0
for bits, counts  in counts_psi.items():
    mean_P += (-1)**(int(bits))* (counts/nshots)

print('<',P,'>','=',np.round(mean_P,5))

/opt/anaconda3/envs/TalentQ/lib/python3.11/site-packages/qiskit/visualization/circuit/matplotlib.py:266: FutureWarning: The default matplotlib drawer scheme will be changed to "iqp" in a following release. To silence this warning, specify the current default explicitly as style="clifford", or the new default as style="iqp".
  self._style, def_font_ratio = load_style(self._style)

Counter({'0': <tf.Tensor: shape=(), dtype=int64, numpy=8421>, '1': <tf.Tensor: shape=(), dtype=int64, numpy=1579>})
< Y > = 0.6842

Finalmente ya estamos en condiciones de calcular el valor esperado de un observable arbitrario

Ejercicio

genera un observable arbitrario \(A\). Obtén los coeficientes \(a_i\) y calcula el valor esperado

\[\begin{eqnarray*} \langle A\rangle_\psi = ~a_0 + a_1 \langle X\rangle_\psi + a_2 \langle Y\rangle_\psi + a_3 \langle Z\rangle_\psi \end{eqnarray*}\]

\(\langle A \rangle\) con un sólo circuito

Podemos escribir la descomposición de \(A\) de la siguiente manera

\[ A = a_0 I + |{\bf a}| ~ \hat \bn \cdot \bsig \]

donde \({\bf a} = (a_1,a_2,a_3)~\) y \(~\hat \bn = {\bf a}/ |{\bf a}|\). De modo que, ahora

\[ \langle A \rangle_\psi = a_0 + |\bf a| \, \langle \bn \cdot \bsig \rangle_\psi \]

Vemos que para calcular \(\langle A \rangle_\psi\) es suficiente con conocer los valores \(a_i = (a_0,{\bf a})\) y un sólo circuito que nos proporcione el valor esperado \(\langle \bn \cdot \bsig \rangle_\psi\).

La clave de este último punto está en usar el medidor efectivo en la dirección \(\hat \bn\)

Con la salida de este circuito, el valor esperado es análogo

\[ \langle \bn \cdot \bsig \rangle_\psi = + \frac{n_0}{N} - \frac{n_1}{N} \]

Ejercicio

utiliza éste metodo para obtener el mismo valor \(\langle A\rangle_\psi \) que en el ejercicio anterior

Valor esperado de un operador unitario

En general el estado \(\ket{\psi}\) debe prepararse a partir del estado \(\ket{0}\). No siempre \(U\) es conocido, pero vamos a suponer que es el caso

\[\ket{\psi} = U_\psi\ket{0}\]

En este caso, podemos calcular el valor esperado de cualquier operador unitario \(V\) de la siguiente forma

\[ \bra{\psi}V\ket{\psi} = \bra{0} U_\psi^\dagger V U_\psi\ket{0} = \braket{0}{\tilde \psi} \]

donde hemos definido el nuevo estado $\(\ket{\tilde\psi} \equiv U_\psi^\dagger V U_\psi\ket{0}\)$

que se prepara mediante un circuito sencillo:

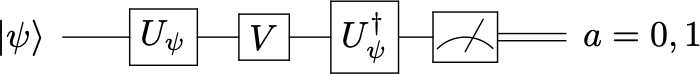
Midiendo \(\ket{\tilde \psi}\) en la base \(Z\), la fracción relativa de resultados \(0\to n_0/N\) nos da acceso al módulo del valor esperado de \(V\).

\[ \sqrt{ \frac{n_{0}(\tilde\psi)}{N} } ~=~ \sqrt{p_0} ~=~ | \braket{0}{\tilde \psi}| ~=~ |\bra{\psi}V\ket{\psi}| ~=~ |\langle V\rangle|_\psi \]

Observable unitario

Si \(V\) además de ser unitario, fuese hermítico, entonces \( \pm \langle V \rangle\) sería una cantidad real. Por este método, al obtener \(|\langle V\rangle |\) sólo perderíamos el signo.

Operadores de 1 cúbit unitarios y hermíticos son, por ejemplo, los operadores \(V = X,Y,Z,H\). Este argumento nos permite calcular de otra manera

\[\begin{split} \left. \begin{array}{c}| \langle Z\rangle_\psi | \\ \rule{0mm}{8mm} | \langle X\rangle_\psi | \\ \rule{0mm}{8mm} | \langle Y\rangle_\psi | \end{array} \right\} ~=~|\braket{0}{\tilde\psi}| ~=~ \sqrt{\frac{n_{0}(\tilde\psi)}{N}} ~~~~~\hbox{con}~~~~~~ \left\{ \begin{array}{l} \ket{\tilde \psi} = U^\dagger Z U\ket{0} \\ \rule{0mm}{8mm} \ket{\tilde \psi} = U^\dagger X U\ket{0} \\ \rule{0mm}{8mm} \ket{\tilde \psi} = U^\dagger Y U\ket{0} \end{array} \right. \end{split}\]

Ejercicio

Calcula por este procedimiento los valores de \(\langle X\rangle_\psi\), \(\langle Y\rangle_\psi\) y \(\langle Z\rangle_\psi\) encontrados anteriormente y verifica que obtienes el mismo resultado.

Qibo

from qibo.models.circuit import Circuit, gates

qc_psi_Qibo = Circuit(1)
qc_psi_Qibo.add(gates.U3(0, theta, phi, 0, trainable=True))

'fijemos el observable a medir'
P = 'Y'

if P =='X':
    qc_psi_Qibo.add(gates.X(0))
elif P=='Y':
    qc_psi_Qibo.add(gates.Y(0))
elif P=='Z':
    qc_psi_Qibo.add(gates.Z(0))

qc_psi_Qibo.add(gates.U3(0, -theta, -phi, 0, trainable=True))

qc_psi_Qibo.add(gates.M(0))
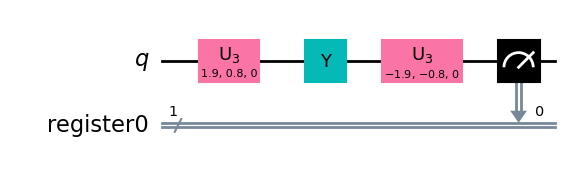
display(tQ.draw_qibo_circuit_mpl(qc_psi_Qibo))

'ejecutamos'
nshots = 10000
counts_psi = qc_psi_Qibo(nshots=nshots).frequencies()
print(counts_psi)

' ahora solo nos interesa la fracción de 0s '
mean_P = np.sqrt(counts['0']/shots)
print('|<',P,'>| =',np.round(mean_P,5))

Qiskit

' el operador unitario que lo genera a partir de |0> es U(theta, phi, 0,0)'
qc_psi_U = QuantumCircuit(1,1)
qc_psi_U.u(theta,phi,0,0)


'fijemos el observable a medir'
P = 'Y'

if P =='X':
    qc_psi_U.x(0)
elif P=='Y':
    qc_psi_U.y(0)
elif P=='Z':
    qc_psi_U.z(0)
    
qc_psi_U.u(-theta,-phi,0,0)


qc_psi_U.measure(0,0)

display(qc_psi_U.draw('mpl'))

' ejecutamos '
shots= 100000
counts=AerSimulator().run(qc_psi_U,shots=shots).result().get_counts()

' ahora solo nos interesa la fracción de 0s '
mean_P = np.sqrt(counts['0']/shots)
print('|<',P,'>| =',np.round(mean_P,5))

Counter({'1': <tf.Tensor: shape=(), dtype=int64, numpy=8663>, '0': <tf.Tensor: shape=(), dtype=int64, numpy=1337>})

---------------------------------------------------------------------------
IndexError                                Traceback (most recent call last)
Cell In[8], line 28
     25 print(counts_psi)
     27 ' ahora solo nos interesa la fracción de 0s '
---> 28 mean_P = np.sqrt(counts['0']/shots)
     29 print('|<',P,'>| =',np.round(mean_P,5))

File /opt/anaconda3/envs/TalentQ/lib/python3.11/site-packages/tensorflow/python/util/traceback_utils.py:153, in filter_traceback.<locals>.error_handler(*args, **kwargs)
    151 except Exception as e:
    152   filtered_tb = _process_traceback_frames(e.__traceback__)
--> 153   raise e.with_traceback(filtered_tb) from None
    154 finally:
    155   del filtered_tb

File /opt/anaconda3/envs/TalentQ/lib/python3.11/site-packages/tensorflow/python/ops/numpy_ops/np_array_ops.py:1721, in _as_index(idx, need_scalar)
   1719 np_dtype = data.dtype.as_numpy_dtype
   1720 if not np.issubdtype(np_dtype, np.integer):
-> 1721   raise IndexError(_SLICE_ERROR + ', got {!r}'.format(idx))
   1722 if data.dtype not in (dtypes.int64, dtypes.int32):
   1723   # TF slicing can only handle int32/int64. So we need to cast.
   1724   promoted_dtype = np.promote_types(np.int32, np_dtype)

IndexError: only integers, slices (`:`), ellipsis (`...`), numpy.newaxis (`None`) and integer or boolean arrays are valid indices, got '0'

Ejercicio

\(X,Y,Z\) y \(H\) son caso particulares de \(\hat\bn\cdot\bsig\) que es también unitario. Escribe el circuito que calcularía \(\langle \hat\bn\cdot\bsig\rangle\) y verifica que da el mismo resultado que obtuviste en un ejercicio anterior.