Tensores sin dolores

Tensores sin dolores#

$ \newcommand{\bra}[1]{\langle #1|} $ $ \newcommand{\ket}[1]{|#1\rangle} $ $ \newcommand{\braket}[2]{\langle #1|#2\rangle} $ $ \newcommand{\ketbra}[2]{| #1\rangle \langle #2|} $ $ \newcommand{\tr}{{\rm tr}} $ $ \newcommand{\i}{{\color{blue} i}} $ $ \newcommand{\Hil}{{\cal H}} $ $ \newcommand{\V}{{\cal V}} $ $ \newcommand{\Lin}{\hbox{Lin}} $

Producto Tensorial#

Un computador clásico es capaz de tratar grandes cantidades de bits a base de acumular dispositivos de un solo bit. Para un computador cuántico consideraríamos una colección de sistemas que implemente, cada uno, un cúbit. Necesitamos describir cómo agrupar sistemas cuánticos.

Supongamos dos sistemas a los que podemos asociar sendos espacios de Hilbert $\Hil_1$ y $\Hil_2$. El sistema cuántico conjunto viene descrito por elementos en el espacio producto tensorial $\Hil =\Hil_1\otimes \Hil_2$. Vamos, a ver cómo se define este espacio vectorial. Empezaremos por sus elementos.

Definición:

dados dos vectores $\ket{u}_1\in \Hil_1$ y $\ket{v}_2\in \Hil_2$, denominamos producto tensorial al par ordenado

\[ \ket{u}_1\otimes \ket{v}_2 \equiv \ket{uv} \]

con la propiedad bilineal, es decir, distributiva

(10)#\[\begin{eqnarray} \big(\ket{u}+\ket{v}\big)\otimes \big(\ket{y}+\ket{z}\big) ~&= &~~ \ket{u}\otimes\ket{y} ~+~ \ket{u}\otimes\ket{z} ~+~ \ket{v}\otimes\ket{y} ~+~~ \ket{v}\otimes\ket{z} \\ \rule{0mm}{8mm} &=& \ket{uy} + \ket{uz} + \ket{vy} + \ket{vz} \end{eqnarray}\]

A continuación construimos un espacio vectorial, que incluya todas las posibles combinaciones lineales de pares ordenados

Definición:

El espacio producto tensorial $\Hil = \Hil_1 \otimes \Hil_2$ está formado por las superposiciones lineales de todas las posibles combinaciones de pares ordenados

\[ \ket{w}= a\ket{u}_1\otimes\ket{u}_2 ~+~ b \ket{v}_1\otimes\ket{v}_2 ~+ ~... \]

donde $\ket{u}_1,\ket{v}_1,...\in \Hil_1\, ~$ y $~\, \ket{u}_2,\ket{v}_2,...\in \Hil_2~$, y $~a,b,... \in {\mathbb C}$ son coeficientes complejos.

Lo que nos dice este teoremas es que al agrupar dos sistemas, los grados de libertad son muchos más que la suma de grados de libertad de cada subsistema. Aparecen todas las posibles combinaciones de estos, y además sus superposiciones lineales.

Base y Dimensión#

Todo esto está muy bien, pero es muy abstracto. Para poder llegar a resultados concretos necesitamos siempre trabajar en una base.

Sucede que, dadas unas bases $\ket{i_1}$ de $\Hil_1$ y $\ket{i_2}$ de $\Hil_2$, automáticamente podemos definir una base en el espacio producto $\Hil_1\otimes \Hil_2$ que se obtiene formando todas las posibles parejas

\[ \ket{i_1 i_2} = \ket{i_1}\otimes \ket{i_2}~~~~~~~~~~~~~~~~~~ \]

con $ i_1=1....d_1$ y $i_2=1,...,d_2 $. Cada elemento así formado es linealmente independiente de los demás. Vemos que las etiquetas de los vectores de la base forman un bi-índice $\to i_1 i_2$ que asume $d_1 d_2$ parejas de valores distintos. El número parejas posibles es $d_1d_2$, que coincide con la dimensión de $\Hil_1\otimes \Hil_2$

Un vector se escribirá igualmente usando $d_1 d_2$ números complejos $w_{i_1 i_2}$, las componentes, etiquetadas ahora mediante un bi-índice en lugar de un índice

\[ \ket{\omega} ~= ~ \sum_{i_1=1}^{d_1}\sum_{i_2=1}^{d_2} w_{i_1i_2} \ket{i_1 i_2} ~=~ w_{11}\ket{11} + w_{12}\ket{12} + ... + w_{21}\ket{21} + ...\ldots + w_{d_1 d_2}\ket{d_1 d_2} \]

Ejemplo

Supongamos que $d_1 = 2$ y $d_2=3$, entonces

\[ \begin{array} \ket{w} &=& w_{11}\ket{11} + w_{12}\ket{12} + w_{13}\ket{13} + w_{21}\ket{21} + w_{22}\ket{22} + w_{23}\ket{23} \end{array} \]

o, en notación matricial

\[\begin{split} \ket{w} ~\sim~ \begin{pmatrix} w_{11}\\ w_{12} \\ w_{13} \\ w_{21} \\ w_{22} \\ w_{23} \end{pmatrix} ~~=~~ \begin{pmatrix} w_{1}\\ w_{2} \\ w_{3} \\ w_{4} \\ w_{5} \\ w_{6} \end{pmatrix} \end{split}\]

Producto de Kronecker#

La matriz columna asociada $\ket{uv}= \ket{u}\otimes \ket{v}$ se forma a partir de las matrices columna de $\ket{u}$ y $\ket{v}$ mediante el denominado producto de Kronecker o, también producto tensorial matricial.

\[\begin{split} \ket{uv} = \ket{u}\otimes \ket{v} ~\sim~ \begin{pmatrix}u_1\\ u_2 \end{pmatrix}\otimes \begin{pmatrix}v_1\\ v_2 \end{pmatrix} ~\equiv ~ \begin{pmatrix}u_1 \begin{pmatrix}v_1\\ v_2 \end{pmatrix} \\ u_2 \begin{pmatrix}v_1\\ v_2 \end{pmatrix} \end{pmatrix} ~=~\begin{pmatrix}u_1v_1\\ u_1v_2 \\ u_2 v_1 \\ u_2 v_2 \end{pmatrix} \end{split}\]

En particular el vector $\ket{ij} = \ket{i}\otimes\ket{j}$ producto de dos elementos de la base sólo tiene una componente igual a 1 en la posición $ij$. Por ejemplo

\[\begin{split} \ket{12} ~=~ \begin{pmatrix}1\\ 0 \end{pmatrix}\otimes \begin{pmatrix} 0\\ 1 \end{pmatrix} ~\equiv ~ ~=~\begin{pmatrix}0\\ 1 \\ 0 \\ 0 \end{pmatrix} \end{split}\]

Notar

Con dos vectores $\ket{u} = \sum_i u_i \ket{e_i}$ y $\ket{v} = \sum_i v_i \ket{e_i} \in \Hil$, hay dos objetos muy parecidos que podemos formar

un operador $\Omega = \ketbra{u}{v} = \sum_{ij}u_i v^*_j\ketbra{e_i}{e_j} \in \Lin(\Hil)$.
un vector \ket{\omega} = \ket{u}\otimes \ket{v} = \sum_{ij} u_i v_j \ket{e_i} \ket{e_j} \in \Hil\otimes \Hil$.

Nota la conjugación compleja relativa entre las dos matrices de componentes $\Omega_{ij} = u^*_i v_j$ y $\omega_{ij} ~=~ u_i v_j$.

Ejercicio (explícaselo a tu ordenador)

escribe una función kronecker(u,v) que tome dos kets (como vectores columna) y devuelva su producto de Kronecker. Verifica el resultado con la funcion $kron$ de numpy.

El entrelazamiento y sus medidas#

Definición: Vector entrelazado

Decimos que, un vector $\ket{w}\in \Hil\otimes\Hil$ es factorizable cuando es posible encontrar vectores $\ket{u},\ket{v}\in \Hil$ tales que $ \ket{w} = \ket{u}\otimes\ket{v}$.

Cuando esto no sea posible, decimos que $\ket{w}$ es un vector entrelazado.

El estado es $\ket{w}$ es factorizable si y sólo si las componentes $w_{ij}$ son factorizables en la forma $w_{ij} = u_i v_j~$ con $i=1,...,d_1$ y $j = 1,...,d_2$.

\[ \ket{w}= \sum_{i,j=1}^d w_{ij} \ket{e_{ij}} = \sum_{i,j} u_{i}v_j \ket{e_i}\otimes \ket{e_j}= \sum_{i,j} u_{i} \ket{e_i}\otimes v_j\ket{e_j} ~ =~ \sum_i u_i\ket{e_i} \otimes \sum_j v_j\ket{e_j} ~=~ \ket{u}\otimes \ket{v} \]

identidad que se puede leer en ambos sentidos. En general no será posible discernir si un vector es factorizable o entrelazado. Vamos a ver algunas herramientas útiles en este sentido.

Nota

Hay muchos más vectores entrelazados que factorizables. El carácter entrelazado de un vector es genérico, mientras que el carácter factorizable es accidental. Esto se sigue de un sencillo contaje:

$\{w_{ij}\}$ forma un conjunto de $d_1d_2$ parámetros complejos independientes (grados de libertad).
sin embargo en $\{u_i v_j\}$ sólo hay $d_1 + d_2$ números independientes.

Es evidente que $d_1 d_2 \gg d_1 + d_2$

La factorizabilidad es una propiedad simple. Se es factorizable o no. El entrelazamiento es una propiedad compleja. Se puede estar más o menos entrelazado. Vamos a ver la manera de caracterizar esto cuando hablamos del producto tensorial de dos espacios de Hilbert.

Concurrencia#

En el caso $d_1 = d_2 =2$ la condición de factorizabilidad $~\Rightarrow ~w_{ij} = u_i v_j$ es equivalente a verificar la anulación del determinante de la matriz $2\times 2$ formada por las componentes

\[\det w_{ij} = w_{11}w_{22}- w_{12}w_{21} = u_1v_1u_2v_2-u_1v_2u_2v_1=0\]

De hecho, la cantidad ${\cal C} = |\det w_{ij}|$ se denomina concurrencia y es parametriza el entrelazamiento de forma monótona

Teorema:

La concurrencia verifica la desigualdad $$ 0\leq {\cal C} \leq 1 $$

El caso ${\cal C}=0$ ya hemos visto que diagnostica que el estado es factorizable. El valor del entrelazamiento de un estado crece con ${\cal C}$ hasta que alcanza su valor máximo posible cuando ${\cal C} = 1$

En el caso general $d_1, d_2 \geq 2$ la busqueda de un criterio para detectar si $w_{ij}$ es factorizable o entrelazado pasa por la descomposición de Schmidt.

Descomposición de Schmidt#

Supongamos que, usando bases $\{\ket{e_{1,i}},~ i=1,...,d_1\}$ de $\Hil_1$ y $\{\ket{e_{2,a}},~a=1,...,d_2\}$ de $\Hil_2$ un cierto vector se escribe

\[ \ket{w} = \sum_{i=1}^{d_1}\sum_{a=1}^{d_2} w_{ia} \ket{e_{1,i}}\otimes \ket{e_{2,a}} \]

Los valores de las componentes $w_{ia}$ dependen de las bases escogida. Si cambiamos a otra base $\ket{ \tilde e_{1,i}}\otimes\ket{\tilde e_{2,a}}$ encontraremos otras componentes $\tilde w_{ia}$ para el mismo vector

Si existe una base en la que $\tilde w_{ia}=0$ para todos los valores de $ia$ menos para uno (por ejemplo $\tilde w_{11}\neq 0$), entonces

\[\ket{w}= \tilde w_{11}\ket{\tilde e_{1,1}}\otimes \ket{\tilde e_{2,1}}\]

y, secretamente, demostraríaos que el vector $\ket{w}$ era factorizable.

El siguiente teorema nos permite averiguar cuánto nos podemos acercar a esta situación

Teorema: de Schmidt

asociadas a cada vector concreto: $\ket{w}\in \Hil_1\otimes \Hil_2$, existen sendas bases $\ket{f_{1,i}}$ de $\Hil_1$ y $\ket{f_{2,a}}$ de $\Hil_2$, tales que, podemos expresar

\[ \ket{w} = \sum_{i=1}^r s_i \ket{f_{1,i}}\otimes\ket{f_{2,i}} \, , \]

donde $s_i>0$, y la suma involucra el mínimo número, $r$, de términos.

El número $1\leq r\leq {\rm min}(d_1,d_2)$ es rango de $w$ y se denomina Número de Schmidt. Es la información relevante porque

cuando $r=1$ el estado $\ket{w}$ será factorizable.
si $r\geq 2$ el estado será entrelazado.

Por tanto, podemos saber si un estado bipartito es entrelazado calculando la descomposición en valores singulares de su matriz de coeficientes en cualquier base.

'Veamos el caso genérico'

d1=4 # Dimensión de H1
d2=3 # Dimensión de H2

' generamos una matriz aleatoria compleja '
w = np.random.randn(d1,d2)+ np.random.randn(d1,d2) * 1j  # coeficientes w_{ia} de un estado genérico
display(array_to_latex(w))

' efectuamos las descomposición SVD'
u, s, vh = np.linalg.svd(w, full_matrices=True)

np.round(s,3)

print('valores principales s_i = ',np.round(s,3))
print('El número de Schmidt es r =', np.count_nonzero(s))

\[\begin{split}\begin{bmatrix} -1.3896636367 + 0.5302254957 i & -0.7608826176 + 1.0708246376 i & -1.0978246021 - 0.6890633895 i \\ -0.7225310549 + 0.8296570057 i & -1.0563594361 + 0.9877826751 i & 1.6622711527 - 0.4317954785 i \\ -0.622093338 + 1.2521929254 i & 0.048530325 + 0.1344251948 i & -2.443265336 - 0.0386277221 i \\ 0.0779504345 + 1.0006217707 i & 2.6915235297 - 0.5890565523 i & 1.6128871997 - 0.7903222963 i \\ \end{bmatrix} \end{split}\]

valores principales s_i =  [4.007 3.584 1.656]
El número de Schmidt es r = 3

Corre la celda anterior muchas veces y mira si consigues encontrar algún caso en que $r<{\rm min}(d_1,d_2)$

'Veamos ahora el caso particular de un estado factorizable'

d1=5
d2=3

' create two random vectors '
u = tQ.random_ket(d1)
v = tQ.random_ket(d2)

w = np.outer(u,v)
display(array_to_latex(w))

' SVG decomposition '
u, s, vh = np.linalg.svd(w, full_matrices=True)

print('principal values s_i = ',np.round(s,3))
print('The Schmidt number is p =', np.count_nonzero(np.round(s,3)))

\[\begin{split}\begin{bmatrix} 0.0948560128 + 0.0280131079 i & -0.03382486 + 0.1250161031 i & -0.2146224742 + 0.0625721777 i \\ 0.191496 + 0.070151258 i & -0.0860871724 + 0.2527915283 i & -0.449889351 + 0.1004584087 i \\ -0.0099293575 + 0.1103348336 i & -0.144736574 - 0.0096869834 i & -0.1158709579 - 0.2219757106 i \\ -0.0554458803 - 0.1737683927 i & 0.2258149047 - 0.0777991127 i & 0.3176834511 + 0.2627765111 i \\ -0.095056773 - 0.147871959 i & 0.1907252249 - 0.12887623 i & 0.3613921824 + 0.1651452318 i \\ \end{bmatrix} \end{split}\]

principal values s_i =  [1. 0. 0.]
The Schmidt number is p = 1

Podemos correr la celda anterior varias veces comprobar que nunca obtendremos $r>1$

Producto Tensorial Múltiple#

El producto tensorial se puede generalizar a más de un factor: el espacio $ \Hil_1\otimes \Hil_2 ... \otimes \Hil_n$ está formado por todas las n-tuplas ordenadas de vectores

\[ \ket{u} = \ket{u_1u_2...u_n} \equiv\ket{u_1}\otimes\ket{u_2}\otimes ...\otimes \ket{u_n} \]

donde $\ket{u_i}\in \Hil_i$, y todas sus combinaciones lineales $\{ a\ket{u}+ b\ket{v} + ...\}$.

Salvo mención expresa, asumiremos que todos los $\Hil_j=\Hil$ son iguales y de dimension $d$. En el contexto de la computación cuántica usual con cúbits $\Rightarrow \, d=2$

Ejercicio

Escribe una función kronecker($u_1,u_2,...,u_n$) que tome n kets (como vectores columna) y devuelva su producto de Kronecker múltiple.

Base de $\Hil^{\otimes n}$#

Una base de $\Hil^{\otimes n}$ se obtiene a partir de cadenas

\[\ket{i_1 i_2.... i_n} = \ket{i_1}\ket{i_2} ... \ket{i_n}\]

donde $i_1,..,i_n=0,...,d-1$. El número de posibles cadenas es $d^n$ que es la dimensión de $\Hil^{\otimes n}$

\[ {\rm dim}_{\mathbb C} \Hil^{\otimes n} = d^n \]

Si cada base $\{\ket{i}\}$ es ortonormal, tendremos que la base del espacio producto también lo será

\[ \braket{i_1 i_2... i_n}{j_1j_2...j_n} = \delta_{i_1j_1}\delta_{i_2j_2}...\delta_{i_nj_n} \]

Ejemplo

Supongamos que $d=3$ (cútrits) y $n=3$ . Entonces $\Hil^{\otimes 3}$ tendría por base, elementos de la forma

\[\{\ket{i j k}\} = \{ \ket{000},\ket{001},\ket{002},\ket{010},....,\ket{332},\ket{333}\}\]

que son ortonormales

\[ \braket{000}{000} = 1~~~,~~~ \braket{000}{001} = 0~~~,..., ~~~ \braket{333}{332} = 0~~~,~~~ \braket{333}{333} = 1 \]

Vectores generales: tensores#

Un vector general $\ket{u}$ de $\Hil^{\otimes n}$ admitirá una expansión en esta base mediante $d^n$ números complejos $u_{i_1 i_2...i_n}$ en la forma

\[ \ket{u} ~~=~ \sum_{i_1,...,i_n=0}^{d-1} u_{i_1i_2...i_n} \ket{i_1i_2...i_n}\, . \]

Podemos recuperar cualquier componente proyectando sobre el elemento correspondiente de la base

\[ u_{i_1i_2...i_n} = \braket{i_1 i_2... i_n}{u} \]

Definición: Tensores

Las cantidades $u_{i_1i_2...i_n}$ forman las componentes de un tensor de rango $n$.

Un tensor de rango $n=1$ es un vector, y un tensor de rango $n=2$ es una matriz.

Un estado genérico depende de un conjunto de $d*d...*d = d^n$ componentes independiente $u_{i_1i_2...i_n}$.

Ya hemos visto los casos de rango $n=1$ (vector) y $n=2$ (operador)

Vector factorizable#

Al igual que antes, sólo en casos muy particulares, un vector de $\Hil^{\otimes n}$ se podrá escribir en forma factorizada

\[ \ket{w} = \ket{v_1}\ket{v_2}\ldots\ket{v_n} \equiv \ket{v_1 v_2 \ldots v_n} \]

Escribiendo $\ket{v_k} = \sum_{i_k=1}^d v_{i_k}\ket{i_k}$ vemos que un vector factorizable admite una expansión general en la que los coeficientes son factorizables

\[ v_{i_1i_2...i_n} = v_{i_1} v_{i_2}.... v_{i_n} \]

El conjunto de coefficientes está parametrizado por $d +d + ...d = nd$ cantidades $v_{i_k}, \, i_k=1,...,d, \, k=1,...,n$.

Un vector no factorizable está entrelazado. El número de dicho vectores crece como el de componentes $w_{i_1,...i_n}$ independientes, esto es como $d^n \gg nd$

Ahora no contamos con un análogo del teorema de Schmidt para averiguar cuándo un vector de $\Hil^n$ es factorizable o entrelazado

El insondable entrelazamiento#

Para estados en el producto tensorial de dos espacios $\Hil = \Hil_1\otimes \Hil_2$ vimos que el número de Schmidt es una forma de caracterizar la cantidad de entrelazamiento. En el caso multipartito esto se vuelve inabarcable. Existen numerosas cantidades, denominadas monónotonos de entrelazamiento que pretenden capturar la profundidad del entrelazamiento.

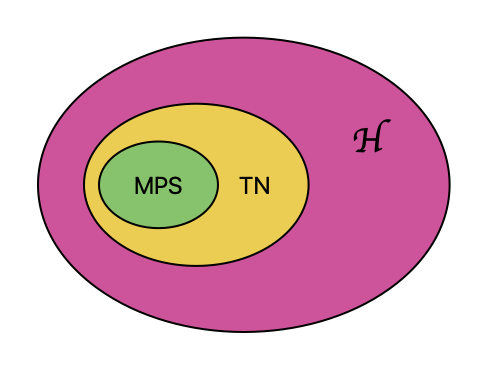
Estados producto de matrices (MPS)#

En medio de los dos casos extremos anteriores encontramos la posibilidad de que las componentes del tensor se puedan escribir como productos de matrices

Definición:

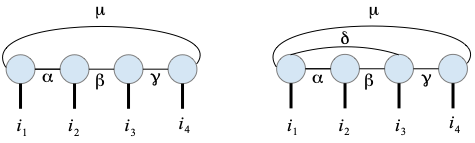
Un estado $\ket{v}$ es un MPS (estado producto de matrices) si sus componentes en cualquier base pueden escribirse como la traza total de un producto de matrices

\[ v_{i_1 i_2 i_3... i_n} =\tr ( A^{(1)}_{i_1}\cdot A^{(2)}_{i_2}\cdot A^{(3)}_{i_3} \cdots A^{(n)}_{i_n} ) \]

Si $A^{(a)}_i$ con $a=1,...,n$ y $i=1,...,d$ es un conjunto de $nd$ matrices de dimensión $D\times D$ decimos que $D\geq 1$ es la (dimensión local de enlace). El número de parámetros independientes es $ndD^2$.

Los MPS tienen entrelazamiento no nulo, que crece con $D$. Cuando $D=1$ volvemos al caso de vectores factorizables.

Si $A^{(a)}_i = A_i$ para todo $a=1,..,n$ decimos que el MPS formado es invariante traslacional. Notar que, en este caso, debido a la ciclicidad de la traza tenemos la igualdad de las componentes relacionadas por una permutación cíclica

\[ v_{i_1 i_2 i_3... i_n} = v_{i_2 i_3... i_n i_1 } = \, ... \]

Por ejemplo, con $n=4$, $\ket{v} = v_{i_1i_2i_3i_4} \ket{e_{i_1i_2i_3i_4} }$

\[ v_{i_1i_2i_3i_4} = \sum_{\alpha\beta\gamma\mu = 1}^DA_{i_1}^{\mu \alpha}A_{i_2}^{\alpha\beta}A_{i_3}^{\beta\gamma}A_{i_4}^{\gamma\mu} \]

Redes de tensores#

Si queremos aumentar el entrelazamiento del estado podemos, además de aumentar $D$,podemos recurrir a sumar (contraer) los índices de tensores de mayor rango

\[ v_{i_1i_2i_3i_4} = \sum_{\alpha\beta\gamma\mu\delta = 1}^D A_{i_1}^{\mu \alpha\delta}A_{i_2}^{\alpha\beta}A_{i_3}^{\beta\delta\gamma}A_{i_4}^{\gamma\mu} \]

La contracción de índices de estos tensores se corresponde con un grafo que puede tener distinta conectividad en distintos nodos

Los estados MPS, y los estados TN para una dimensión de enlace local $D$ finita, no son suficientemente expresivos para capturar el máximo entrelazamiento posible en los estados más geneales de $\Hil$

Notar

$nd \ll d^n$. El crecimiento exponencial del número de estados entrelazados es el ingrediente crucial para la computación cuántica. Observar que $d^n$ es el número de enteros alcanzables por $n$ bits. Pero en computación cuántica es el número de dimensiones en la que podemos poner $d^n$ amplitudes complejas.
No existe un criterio general para saber si un estado es, a priori, factorizable o entrelazado.
Además, hay formas de caracterizar matemáticamente el nivel de entrelazamiento (entanglement witnesses, entanglement monotones etc.) desde nulo (estado factorizable) hasta maximal.

Operadores sobre $\Hil^{\otimes n}$#

El espacio $\Hil^{\otimes n}$ admite, como cualquier espacio vectorial, la acción de operadores lineales $A: \Hil^{\otimes n} \to \Hil^{\otimes n}$ donde

\[ A:\ket{u} \to \ket{v} \equiv A\ket{u} \]

El conjunto de todos los operadores lineales forman el espacio vectorial $\Lin(\Hil^{\otimes n})$

Matrices#

A cada operador, $A$, le podemos asociadar una matriz, una vez elijamos nuestra base $\{ \ket{i_1 i_2... i_n}\}$ donde, $i_k = 1,...,d$. Los elementos de matriz ahora vendrán etiquetados por dos multi-índices

\[ A_{i_1...i_n, \, j_1...j_n} = \bra{i_1...i_n}A\ket{j_1...j_n} ~~~~~\leftrightarrow ~~~~~~ A_{ab}= \bra{a}A\ket{b} \]

Con la matriz, el operador se reconstruye en la base canónica de productos externos

(11)#\[\begin{eqnarray} A &~~=~& \sum_{i_1,...,i_n,\, j_1,...,j_n=0}^{d-1} A_{i_1...i_n, \, j_1...j_n} \ket{i_1...i_n}\bra{j_1...j_n} ~~~~=~~~~ \sum_{a,b=a}^{d^{N}-1} A_{ab} \ket{a}\bra{b} \end{eqnarray}\]

En $A_{i_1...i_n,\,j_1...j_n} = A_{ab}$ hay $d^n\times d^n = d^{2n}$ grados de libertad. Esta sería la dimensión del espacio $\Lin(\Hil^{\otimes n})$.

Οperadores factorizables#

En $\Lin(\Hil^{\otimes n})$ hay un análogo de los vectores factorizables de $\Hil^{\otimes n}$: los operadores factorizables. Decimos de un operador factorizable que es producto tensorial de operadores.

Supongamos $n$ operadores lineales $A^{(a)}\, ,\, a=1,...,n$ definidos sobre cada espacio factor $\Hil$.

Definición:

La acción del producto tensorial de operadores $A = A^{(1)}\otimes A^{(2)} \otimes ...A^{(n)}$ sobre un vector $\ket{v} = \ket{v}_1\otimes ...\otimes \ket{v_n}\in \Hil~$ es

\[ A\ket{v} = A^{(1)}\ket{v_1}\otimes ... \otimes A^{(n)} \ket{v_n}\, . \]

En un producto tensorial de operadores el adjunto se toma en cada factor sin permutar el orden

\[ A^\dagger = A^{(1)\dagger} \otimes ... \otimes A^{(n)\dagger} \]

El producto tensorial de operadores hermíticos es hermítico

\[ A^{(a)\dagger} = A^{(a)} ~~\Longrightarrow A^{\dagger} = A \]

El producto tensorial de operadores unitarios, es unitario

\[ A^{(a)\dagger} = A^{(a)\, -1} \, ~~\Longrightarrow ~~A^{\dagger} = A^{-1} \]

Producto de Kronecker de matrices#

¿Cómo será la matriz $A_{i_1...i_n, \, j_1...j_n}$ de un operador factorizable, $ A = A^{(1)}\otimes A^{(2)} \otimes ...A^{(n)}$, en términos de las matrices $ A^{(a)}_{ij}$ de sus factores?

Vamos a tomar $n=2$ por simplicidad

\[\begin{eqnarray*} A = A^{(1)}\otimes A^{(2)} &=&\left( \sum_{i_1i_2}A^{(1)}_{i_1 j_1} \ket{i_1}\bra{j_1}\right)\left( \sum_{i_2j_2}A^{(2)}_{i_2 j_2} \ket{i_2}\bra{j_2}\right)\\ &=& \sum_{i_1 i_2 , j_1 j_2} A^{(1)}_{i_1 j_1}A^{(2)}_{i_2 j_2}\ket{i_1 i_2}\bra{j_1j_2} \\ &=& \sum_{i_1 i_2 , j_1 j_2} A_{i_1i_2,\, j_1j_2}\ket{i_1 i_2}\bra{j_1j_2} \end{eqnarray*}\]

Vemos que la matriz asociada a $A$ se obtiene a partir de las matrices de $A^{(a)}$ mediante el producto exterior de las matrices, o producto de Kronecker.

\[ A_{i_1i_2,\,j_1j_2} = A^{(1)}_{i_1j_1}A^{(2)}_{i_2 j_2} \]

El método para de representar matricialmente el producto de Kronecker de dos matrices $A\otimes B$ es sencillo. Supongamos que $d=2$ y tenemos un operador producto $A\otimes B$. Entonces su matriz

\[\begin{split} (A\otimes B)_{ab} = \begin{pmatrix} A_{00}B & A_{01}B \\ A_{10}B & A_{11}B \end{pmatrix} = \begin{pmatrix} A_{00}B_{00} & A_{00}B_{01} & A_{01}B_{00} & A_{01}B_{01} \\ A_{00}B_{10} & A_{00}B_{11} & A_{01}B_{10} & A_{01}B_{11} \\ A_{10}B_{00} & A_{10}B_{01} & A_{11}B_{00} & A_{11}B_{01} \\ A_{10}B_{10} & A_{10}B_{11} & A_{11}B_{10} & A_{11}B_{11} \end{pmatrix}. \end{split}\]

El producto de Kronecker verifica las siguientes propiedades para dos matrices $A$ y $B$ de dimensiones $d_A$ y $d_B$.

\[\begin{eqnarray*} (A\otimes B)(C\otimes D) &=& (AC)\otimes (BD) \nonumber\\ \rule{0mm}{6mm} \tr(A\otimes B) &=& (\tr A)(\tr B) \nonumber\\ \rule{0mm}{6mm} A\otimes(B+D) &=& A\otimes B + A\otimes D \nonumber\\ \rule{0mm}{6mm} (A\otimes B)^\dagger &=& A^\dagger\otimes B^\dagger \nonumber\\ \rule{0mm}{6mm} (A\otimes B)^{-1} &=& A^{-1} \otimes B^{-1} \nonumber\\ \rule{0mm}{6mm} \det (A\otimes B) &=& (\det A)^{d_B}(\det B)^{d_A} \end{eqnarray*}\]

donde $AC$ significa el producto de matrices $A$ y $C$

La generalización a todo $n$ es obvia. El producto de Kronecker de $n$ matrices $ A^{(a)}_{i_aj_a}$ asociadas a operadores $A^{(a)}$ es

\[ A_{i_1...i_n,\,j_1...j_n} = A^{(1)}_{i_1j_1}...A^{(n)}_{i_n j_n} \]

Notar

Observar que en un operador general, la matriz $ A_{i_1...i_n,\,j_1...j_n}$ tiene $d^n\times d^n = d^{2n}$ entradas independientes.

Sin embargo en un producto de Kronecker $A^{(1)}_{i_1j_1}...A^{(n)}_{i_n j_n}$ sólo hay $nd^2$.

Por tanto, los operadores factorizables forman un subconjunto muy pequeño dentro del conjunto de los operadores generales.

Ejercicio

Demuestra estos resultados.
Rescribe la función $kronecker$ para que acepte dos matrices $A$ y $B$ de dimensiones $d_A$ y $d_B$ y devuelva su producto de Kronecker $A\otimes B$. Verifica el resultado con la funcion kron de numpy. Verifica las propiedades anteriores.

Ejercicio

Calcula $\sigma_1\otimes \sigma_2\otimes \sigma_3$

Generación de entrelazamiento#

Supongamos que $\ket{u} = \ket{u_1}\otimes\ket{u_2}$ es factorizable.

Si $A=A_1\otimes A_2$ es un operador factorizable entonces

<br

\[ \ket{v} = A\ket{u} = A_1\ket{u_1}\otimes A_2\ket{u_2} = \ket{v_1}\otimes \ket{v_2} \]

también es factorizable.

Inversamente, la acción de un operador no factorizable $A\neq A_1\otimes A_2$ genera estados entrelazados

\[ \ket{v} = A\ket{u} \neq \ket{v_1}\otimes \ket{v_2} \]

En lenguaje físico, lo que esto quiere decir es que para generar entrelazamiento debe haber interacción entre los grados de libertad que residen en $\Hil_1$ y $\Hil_2$. Si no hay interacción, estados factorizados seguiran siendo factorizables en el futuro.

Tensores sin dolores

Contents

Tensores sin dolores#

Producto Tensorial#

Base y Dimensión#

Producto de Kronecker#

El entrelazamiento y sus medidas#

Concurrencia#

Descomposición de Schmidt#

Producto Tensorial Múltiple#

Base de \(\Hil^{\otimes n}\)#

Vectores generales: tensores#

Vector factorizable#

El insondable entrelazamiento#

Estados producto de matrices (MPS)#

Redes de tensores#

Operadores sobre \(\Hil^{\otimes n}\)#

Matrices#

Οperadores factorizables#

Producto de Kronecker de matrices#

Generación de entrelazamiento#