Fundamentos de Mecánica Cuántica

Fundamentos de Mecánica Cuántica#

$ \newcommand{\bra}[1]{\langle #1|} $ $ \newcommand{\ket}[1]{|#1\rangle} $ $ \newcommand{\braket}[2]{\langle #1|#2\rangle} $ $ \newcommand{\ketbra}[2]{| #1\rangle\! \langle #2|} $ $ \newcommand{\tr}{{\rm tr}} $ $ \newcommand{\i}{{\color{blue} i}} $ $ \newcommand{\Hil}{{\cal H}} $ $ \newcommand{\V}{{\cal V}} $

Ha llegado el momento de desvelar las verdaderas reglas del juego. En este capítulo veremos los postulados de la Mecánica Cuántica, y te pasará lo que nos pasa a todos: que no hay quien los entienda. Pero así es: la Mecánica Cuántica es un conjunto de prescripciones acerca de cómo manipular la (escasa) información que es posible extraer de los sistemas microscópicos. Lo importante es que hace predicciones sobre resultados de medidas que se verifican. En cuanto a lo otro: al final nos acostumbramos a pensar de la manera en que la MC dice que tiene sentido hacerlo, y a eso le llamamos entender.

Los axiomas de la Mecánica Cuántica son sus pilares. Todo se deriva de ellos. Y, como todos los axioma, son de origen heurístico, es decir, basados en la experimentación. La axiomática comúnmente aceptada es la denominada interpretación de Copenhagen. Empezamos.

Axiomas de la Mecánica Cuántica para Sistemas Aislados#

Estado del sistema

Postulado I: Vector de estado

En un instante, $t$, la máxima información accesible de un sistema cuántico aislado está asociada a un vector $\ket{\psi}$ de norma unidad, perteneciente a un espacio de Hilbert $\Hil$. Dos vectores que difieran en una fase representan al mismo estado. Es decir, son físicamente indistinguibles.

La palabra estado es engañosa por cuanto parece indicar que el sistema está definido en cada instante por un valor concreto de sus propiedades. ¡Esto no es así! El vector de estado se conoce también con el nombrede función de onda

El postulado I lleva una pequeña pero importante puntualización: dos vectores que difieran en una fase global contienen idéntica información y, por tanto, representan al mismo estado: ningún experimento permite distinguirlos. Es decir

\[ \ket{\psi} \sim \ket{\psi'} = e^{i\varphi}\ket{\psi} \, , \]

Evolución con el tiempo

La dinámica de un sistema cuántico está codificada en un operador hermítico $H = H^\dagger$ que se denomina operador Hamiltoniano. El Hamiltoniano gobierna la evolución. Supongamos que el sistema se prepara a $t=0$ en un cierto estado $\ket{\psi(0)}$

Postulado II: Evolución con el tiempo

El cambio continuo en el tiempo de $\ket{\psi(t)}$ de un sistema cuya dinámica obedece a un Hamiltoniano $H(t)$, es determinista y es solución de la Ecuación de Schrödinger

\[ \frac{\partial\ket{\psi(t)}}{\partial t} =-\frac{i}{\hbar} H(t) \ket{\psi(t)} \, \label{eqschr} \]

La ecuación de Schrödinger es una ecuación diferencial ordinaria (una sola variable) para un vector. Para una condición inicial dada $\ket{\psi(t=0)} = \ket{\psi_0}$, la solución $\ket{\psi(t)}$ para todo $t$ es única.

Medidas

Por tanto, la evolución del estado es determinista. Es en la medida sobre el sistema donde la Mecánica Cuántica muestra su carácter probabilístico. Vamos a mencionar en este capítulo la medida proyectiva, que es el caso más simple. Estudiaremos en el capítulo 5 que son un caso particular del tipo más general de medidas posible

Postulado III: Medidas proyectivas, o de Von Neumann

A una magnitud física medible le está asociado un operador hermítico $ A= A^\dagger$ que denominamos observable.
Los resultados de una medición solo pueden dar como resultado uno de los valores propios de $A \Rightarrow \lambda_k$.
Regla de Born: La probabilidad de obtener el autovalor $\lambda_k$ como resultado de una cierta medición, viene dada por la expresión

\[ p(\lambda_k)~ = ~|\braket{\lambda_k}{\psi}|^2 \]

donde $\ket{\lambda_k}$ es el autovector asociado.

Este postulado establece el nexo entre el formalismo matemático y la experimentación física. Y pone en el centro la naturaleza probabilística del las predicciones: la función de onda, en el fondo es una especie de raíz cuadrada de una distribución de probabilidad.

La norma unidad del vector de estado postulada en el axioma 1 es consistente con dicha intepretación probabilística. Efectivamente como la suma de todas las probabilidades debe ser igual a uno

\[ 1 = \sum_k \lambda_k = \sum_k \braket{\psi}{\lambda_k}\braket{\lambda_k}{\psi} = \bra{\psi}\left(\sum_k\ketbra{\lambda_k}{\lambda_k}\right) \ket{\psi} = \braket{\psi}{\psi} \]

Que las magnitudes medibles son números reales, exige que el operador $A$ asociado a un observable deba ser hermítico

Nota

Muy importante: $\{\lambda_k,p(\lambda_k)\}$ no es una variable pseudo-aleatoria sino, probablemente, la única variable intrínsecamente aleatoria que existe en la naturaleza.
La fórmula dada para $p(\lambda_k)$ es cierta cuando el autovalor en cuestion es no degenerado. Cuando $\lambda_k$ tiene degeneración $d_k$ debe generalizarse:

\[\begin{split} \begin{array}{rcl} p(\lambda_k)~ &=& ~ \sum_{a=1}^{d_k}|\braket{\lambda^a_k}{\psi}|^2 = \bra{\psi}\left( \sum_{a=1}^{d_k}\ketbra{\lambda^a_k}{\lambda^a_k}\right) \ket{\psi}\nonumber\\ &=& \bra{\psi}P_k\ket{\psi} \rule{0mm}{7mm}\\ \end{array} \end{split}\]

La última expresión revela que $p(\lambda_k)$ no es más que el valor esperado del proyector $P_k = P^2_k$ en el estado del sistema anterior a la medida.

Colapso de la función de onda

La función de onda sufre una variación abrupta en el momento de medir. Es, con la variación contínua del Postulado II, la única forma de cambio que puede experimentar el estado de un sistema.

Postulado IV: Colapso de la función de onda

Si el resultado de una medida efectuada sobre un sistema en un estado $\ket{\psi}$ ha sido $\lambda_n$, inmediatamente después de la medida, el estado del sistema viene dado por el vector propio asociado
$\ket{\lambda_n} \in \Hil$, normalizado $|\braket{\lambda_n}{\lambda_n}|=1$

Este colapso no es distinto en esencial del que sufre una distribución de probabilidad cuando se añade información fruto de un experimento. Por ejemplo, una distribución $(1/2,1/2)$ describe nuestra total ignorancia acerca de bajo qué cubilete se esconde la bola de un trilero. En cuanto levantamos uno, dicha distribución pasa abrúptamente a ser de total certeza $(1,0)$ ó $(0,1)$ dependiendo de cada caso.

Hay dos peculiaridades que distinguen el caso cuántico y estimulan la especulación filosófica.

Una ocurre cuando el sistema que se mide está compuesto de partes en un estado cuántico entrelazado. Una medida en una parte induce un colapso también en la otra, y eso independientemente de la naturaleza de, o la distancia a, dicho otro subsistema. De aquí surge famosas paradojas como la del gato de Schrödinger o la de EPR.

La otra es que el sistema del medidor y el medido pueden verse a su vez como partes de un sistema aislado.
¿Qué marca la diferencia entre el sistema que mide y el que colapsa? ¿cuál es el límite entre un objeto cuántico y uno clásico?

Medidas y valores esperados#

En Mecánica Cuántica especificamos un estado en las componentes de la expansión de un estado en una base ortonormal. Existen infinitas bases posibles para expresar un vector. ¿Qué base es la mejor? La respuesta es que depende del proceso que estudiemos.

Por ejemplo, si el proceso es la medida de un cierto observable $A=A^\dagger$, el resultado de nuestra medición sólo puede ser uno de los valores propios $\lambda_i$

\[ A \ket{\lambda_k} = \lambda_k \ket{\lambda_k}\, \]

donde $\ket{\lambda_k}$ son los autovectores ${k=1,2,...}$ que forman una base ortonormal. Ésta es la base natural adaptada a procesos de medida de $A$. En particular para conocer con qué probabilidad se producirá cada resultado, expandiremos el estado en dicha base de autoestados

\[ \ket{\psi} = \sum_{i=1}^N a_i \ket{\lambda_i}\, \]

El axioma IV (regla de Born) afirma que la probabilidad de aparición del resultado $\lambda_i$ es precisamente

\[ p(\lambda_i)=|\braket{\lambda_i}{\psi}|^2 = |a_i|^2 \, \]

La forma de tener acceso experimental a los números $p(\lambda_i)$ es mediante la repetición estadística. Si efectuamos la medida un número $n$ de veces con $n\to \infty$, y contamos la frecuencia de aparición de los distintos $\lambda_i$ en el límite $n\to \infty$ dicha frecuencia experimental convergerá a la probabilidad teórica

\[ \lim_{n\to\infty} \frac{n(\lambda_i)}{n} = p(\lambda_i) = |a_i|^2 \, . \]

Vemos que, mediante repetición estadística, solamente podemos recuperar el módulo de las amplitudes

\[ |a_i| = \lim_{n\to\infty} \sqrt{\frac{n(\lambda_i)}{n} } \]

Notar

En Computación Cuántica, almacenamos la información en las amplitudes $a_i$ en una base dada (la base computacional). Vemos que sólamente su módulo $|a_i|$ es recuperable a través de medidas.
Cada vez que seleccionamos un estado $\ket{\psi}$, y un observable $A$, se genera una variable aleatoria $(\lambda,p(\lambda))\, \to $ en cada medida de $A$ sobre $\ket{\psi}$ obtenemos un autovalor $\lambda_i$ con una probabilidad $p(\lambda_i)$. La repetición del experimento permite reconstruir estimadores estadísticos.

Ejercicio

Generaliza las expresiones anteriores al caso en que los autovalores $\lambda_k$ puedan ser $d_k$ veces degenerados.

Valores esperados#

Rescribamos la probabilidad de encontrar $\lambda_k$ en el caso de que sea $d_k$ veces degenerado

\[\begin{split} \begin{array}{rcl} p(\lambda_k) &=& \sum_{a=1}^{d_k} |\braket{\lambda^a_k}{\psi}|^2 = \sum_{a=1}^{d_k} \braket{\psi}{\lambda^a_k}\braket{\lambda^a_k}{\psi} \nonumber\\ \rule{0mm}{8mm} &=&\bra{\psi} \left( \sum_{a=1}^{d_k} \ket{\lambda^a_k}\bra{\lambda^a_k} \right) = \bra{\psi}P_k \ket{\psi} \end{array} \end{split}\]

donde

\[ P_k = \sum_{a=1}^{d_k} \ket{\lambda^a_k}\bra{\lambda^a_k} \]

es el proyector sobre el subespacio propio. Por el valor esperado $\langle A\rangle$ del observable $A$ en el estado $\ket{\psi}$, entendemos el valor medio de la variable aleatoria $\lambda_n$ obtenida por el método descrito.

(14)#\[\begin{eqnarray} \langle A\rangle &= & \sum_k \lambda_k p(\lambda_k) = \sum_k \lambda_k \bra{\psi}P_k\ket{\psi} &=& \bra{\psi}\left(\sum_k \lambda_k P_k \right) \ket{\psi} \end{eqnarray}\]

Reconocemos entre paréntesis la descomposición espectral de $A$. Llegamos así a la siguiente expresión para el valor esperado de un observable $A$ en un estado $\ket{\psi}$

Teorema:

\[\langle A \rangle=\bra{\psi}A \ket{\psi} \]

En particular, las probabilidades mismas se pueden expresar como valores esperados del proyector asociado

\[ p(\lambda_k ) = \bra{\psi}P_k\ket{\psi} = \langle P_k\rangle \]

El espectro de un observable está formado por números reales que podemos ordenar $\lambda_{min}<...<\lambda_{max}$. El valor esperado de un observable en uno de sus autoestados coincide con el autovalor asociado

\[ \bra{\lambda_i}A \ket{\lambda_i} = \bra{\lambda_i}\lambda_i \ket{\lambda_i} = \lambda_i \braket{\lambda_i}{\lambda_i} = \lambda_i \]

Desviación estándar#

La varianza es la media de la desviación cuadrática de la variable aleatoria $(\lambda,p(\lambda))$ es decir

\[ ~~\sigma ^2 = \overline{(\lambda_i-\bar\lambda_i)^2}= \overline{\lambda^2} - \overline{\lambda}^2 \]

de aquí se sigue, para la desviación estándar.

Teorema:

\[ \sigma = \sqrt{\bra{\psi}A^2\ket{\psi} - \bra{\psi} A\ket{\psi}^2} \]

Evaluada en un estado propio $\ket{\lambda_i}$, la varianza de un operador es cero

\[ \sigma^2 = \bra{\lambda_i}A^2\ket{\lambda_i} - \bra{\lambda_i} A\ket{\lambda_i}^2 = \bra{\lambda_i}\lambda_i^2\ket{\lambda_i} - \bra{\lambda_i} \lambda_i\ket{\lambda_i}^2 = 0 \]

' función que toma una matriz y un vector normalizado  y devuelve el valor esperado y la desviación '
def vev_sig(A, ket):
    
    'verificamos norma unidad del ket'
    assert np.round(np.sqrt(np.dot(ket.conj().T,ket)[0,0]).real,5)  == 1.
    bra = ket.conj().T
    
    'el valor esperado'
#    vev = np.dot(bra,np.dot(A,ket))[0,0].real
    vev = tQ.braket(ket,np.dot(A,ket))
    
    'la varianza'
    A2 = np.dot(A,A)
    var= tQ.braket(ket,np.dot(A2,ket)) - vev**2
    sig = np.sqrt(np.abs(var.real))
    
    return(np.round(vev,5), np.round(sig,10))

' definamos una matriz hermítica '
#np.random.seed(10) 
A = np.matrix(np.random.randn(3,3) + np.random.randn(3,3)*1j)
A +=  A.getH()
eigvals, eigvecs = np.linalg.eigh(A)
' mostramos los autovalores '
np.round(eigvals,4)

array([-2.7491,  0.8194,  5.5336])

A continuación evaluamos el valor esperado en un vector aleatorio, y en dos autovectores de $A$

'definamos un ket'
vec1 = np.random.randn(len(A),1)   # este es un autovector aleatorio
vec2 = eigvecs[:,0]           # este es el autovector de autovalor mínimo
vec3 = eigvecs[:,-1]          # éste es un autovector de autovalor máximo

ket = vec2       # elegimos uno 

'normalizado'
norma=np.sqrt(np.dot(ket.conj().T,ket)[0,0]).real 
uket = ket/norma


vev, sig = vev_sig(A,uket)

print('<A>= ',vev, ' sigma = ', sig)

<A>=  (-2.74909-0j)  sigma =  7.88e-08

Evolución temporal#

Ecuación de Schrödinger#

El estado de un sistema $\ket{\psi(t)}$ posee la máxima información instantánea accesible de un sistema, es decir, a un tiempo dado $t$. Dado $\ket{\psi(t_0)}$ en un instante inicial $t_0$, la evolución posterior obedece a la ecuación diferencial de Schrödinger

\[ \displaystyle \frac{d}{d t}\ket{\psi(t)} =-\frac{i}{\hbar} H(t) \ket{\psi(t)} \, . \]

Hemos enfatizado el hecho de que, en el caso más general, $H(t)$ puede depender del tiempo.

Notar

Las cantidades que entran en la ecuación de Schrödinger tienen unidades:

$H$ tiene unidades de energía. En el SI (Sistema Iternacional) $\to$ $\hbox{Julios = J}$
$t$ tiene unidades de tiempo, en el SI $\to$ $\hbox{segundos = s}$
$\hbar$ es la constante de Planck, y tiene unidades de acción= energía $\times$ tiempo. En el SI $\to $ $\hbox{Julios}\cdot\hbox{segundo} = \hbox{J}\cdot\hbox{s}$. $~$ Se trata de una cantidad universal $$ \boxed{\hbar = 1.054\times 10^{-34}~~ \hbox{J}\cdot\hbox{s}} $$

Conservación de la probabilidad.#

La hermiticidad de $H$ se relaciona directamente con la interpretación probabilística de $\ket{\psi}$.

Teorema:

En la evolución temporal se conserva la norma del vector de estado

Operador de Evolución#

La conservación de la norma implica que la evolución $\|\ket{\psi(0)\|} =\|\ket{\psi(t)}\|$ es un proceso unitario. En otras palabras, debe existir un operador unitario

\[ U(t,t_0)^{-1}= U(t,t_0)^\dagger \]

que lleve el estado inicial al actual a tiempo $t$

\[ U(t,t_0): \ket{\psi(t_0)}~~ \to~~ \rule{0mm}{3.5mm} \ket{\psi(t)} = U(t,t_0)\ket{\psi(t_0)} \]

Notar

El operador de evolución satisface las siguientes propiedades

$U(t_0,t_0) = I$ , .
transitividad: $U(t,t_1)U(t_1,t_0)= U(t,t_0)$
invertibilidad: $U(t,t_0)^{-1} = U(t_0,t)$

Evidentemente, el operador de evolución debe estar relacionado con el Hamiltoniano, que es quien gobierna la dinámica. Veamos a ver que hay una ecuación de Schrödinger también para el operador de evolución

Teorema:

El operador de evolución satisface la siguiente ecuación de evolución

\[ \frac{d}{dt}U(t,t_0) = -\frac{i}{\hbar} H(t)\, U(t,t_0) \]

$H$ independiente del tiempo#

Cuando $H$ no depende del tiempo podemos dar una expresión analítica para el operador de evolución

Teorema:

Para un hamiltoniano $H$ independiente del tiempo, el operador de evolución $U(t,t_0)$ es

\[ U(t,t_0) = \exp\left({-\frac{i}{\hbar} (t-t_0)H}\right) \]

Notar

que la cantidad ${-\frac{i}{\hbar} (t-t_0) H }$ es adimensional

\[ \frac{1}{\hbox{J}\cdot \hbox{s}}\hbox{s}\cdot\hbox{J} = 1 \]

Es decir, es un número puro. Por eso podemos exponenciarla. El operador de evolución $U(t,t_0)$ es, por tanto, también, una magnitud adimensional.

Ejercicio

Escribe una función psi(t,psi0,H) que reciba como argumentos el array psi0 de componentes de $\ket{\psi(0)}$, una matriz hermítica H, y un valor de t, y devuelva un vector columna correspondiente a $\ket{\psi(t)}$. Considera $\hbar=1$.

def psi(t,psi0,H):
    lpsi = len(psi0)
    lH = H.shape[0]
    assert lpsi == lH
    
    psi0ket =np.array(psi0).reshape(lpsi,1)
    psitket = np.dot(expm(- 1j*t*H),psi0ket)
    return psitket

Ejercicio

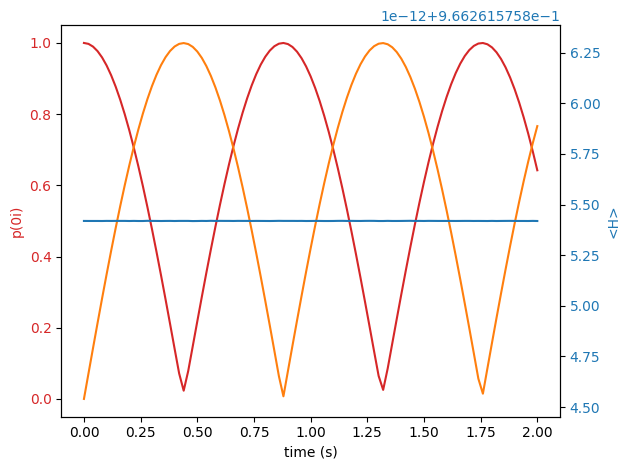
Crea un Hamiltoniano aleatorio $2\times 2$ y considera que la base en la que está escrito es $\{\ket{0},\ket{1}\}$. Partiendo de cualquiera de ellos, grafica las probabilidades de permanencia $p(\ket{0}\to \ket{0})$ y de transición $p(\ket{0}\to \ket{1})$ como funciones del tiempo (considera que $\hbar = 1$ por simplicidad). Grafica también el valor esperado de $H$ en ambos estados como función del tiempo. Observa el resultado e intenta explicar por qué es así.

from matplotlib import pyplot as plt
from scipy.linalg import expm

' definamos un Hamiltoniano '
A = np.random.randn(2,2) + np.random.randn(2,2)*1j
A = np.asmatrix(A)
H = A + A.getH()

'estado inicial |psi(0)>'
psi0 = [1,0]

tend = 2
steps = 100
tlist= np.linspace(0,tend, steps + 1)

'estado a tiempo t |psi(t)>'
psitketlist = [psi(tlist[i],psi0,H) for i in range(len(tlist))]

'probabilidades'
p00list = [np.abs(psitketlist[i][0,0])  for i in range(len(tlist))]
p01list = [np.abs(psitketlist[i][1,0])  for i in range(len(tlist))]

'valores esperados <H>(t)'
psitbralist= [psitketlist[i].conj().reshape(1,2) for i in range(len(tlist))]
Hvevtlist = [np.dot(psitbralist[i],np.dot(H,psitketlist[i])).real[0,0] for i in range(len(tlist))]

Graficamos

fig, ax1 = plt.subplots()

color = 'tab:red'
ax1.set_xlabel('time (s)')
ax1.set_ylabel('p(0i)', color= 'tab:red')
ax1.plot(tlist,p00list, color= 'tab:red')
ax1.plot(tlist,p01list, color= 'tab:orange')
ax1.tick_params(axis='y', labelcolor='tab:red')

ax2 = ax1.twinx()  # instantiate a second axes that shares the same x-axis

color = 'tab:blue'
ax2.set_ylabel('<H>', color='tab:blue')  # we already handled the x-label with ax1
ax2.plot(tlist,Hvevtlist, color='tab:blue')
ax2.tick_params(axis='y', labelcolor='tab:blue')

fig.tight_layout()  # otherwise the right y-label is slightly clipped
plt.show()

../../_images/089dc1b20005707bbe0a459b93dbb0e1106e44af2da4a28c6cda531959088c96.png

Evolución en la base autoestados de H#

La forma más eficaz de calcular la evolución de un estado arbitrario es expresarla en la base $\{\ket{n}\}$ de autoestados de $H \, \Rightarrow \,H \ket{n} = E_n \ket{n}~~~~n=1,..,N.$ $~$ En esta base, $H$ es una matriz $H_{mn}$ diagonal

\[\begin{split} H_{mn} = \begin{bmatrix} E_0 & & & \\ & E_1 & & \\ & & \ddots & \\ & & & \end{bmatrix} =E_m \delta_{mn} \, . \end{split}\]

Entonces la matriz de evolución es también diagonal

\[\begin{split} U_{mn} = \exp\left(-\frac{i}{\hbar}t H_{mn}\right) = \begin{bmatrix} e^{-\frac{i}{\hbar}t E_0} & & & \\ & e^{-\frac{i}{\hbar} t E_1} & & \\ & & \ddots & \\ & & & \end{bmatrix} = e^{-\frac{i}{\hbar} t E_m }\delta_{mn} \, . \end{split}\]

La evolución temporal de un autoestado de la energía es trivial (es una fase global)

\[ U(t,0)\ket{n} = e^{-\frac{i}{\hbar} t E_n} \ket{n}\, . \]

Esta fase deja de ser trivial cuando afecta a una combinación lineal. . Es decir, si a $t=0$ $ \ket{\psi(t=0)} = \sum_n c_n \ket{n} \, , $ entonces, a tiempo $t$

\[ \ket{\psi(t)} = \sum_n c_n e^{-\frac{i}{\hbar}E_n} \ket{n} \, . \]

Fundamentos de Mecánica Cuántica

Contents

Fundamentos de Mecánica Cuántica#

Axiomas de la Mecánica Cuántica para Sistemas Aislados#

Medidas y valores esperados#

Valores esperados#

Desviación estándar#

Evolución temporal#

Ecuación de Schrödinger#

Conservación de la probabilidad.#

Operador de Evolución#

\(H\) independiente del tiempo#

Evolución en la base autoestados de H#