Jun 11, 2024 | 8 min read

Multi-cúbits#
\( \newcommand{\bra}[1]{\langle #1|} \) \( \newcommand{\ket}[1]{|#1\rangle} \) \( \newcommand{\braket}[2]{\langle #1|#2\rangle} \) \( \newcommand{\i}{{\color{blue} i}} \) \( \newcommand{\Hil}{{\mathcal H}} \) \( \newcommand{\cg}[1]{{\rm C}#1} \)
Show code cell source
%run ../../macro_tQ.py
import sys
sys.path.append('../../')
import macro_tQ as tQ
import numpy as np
import scipy.linalg as la
from IPython.display import display,Markdown,Latex
import matplotlib.pyplot as plt
from qiskit.visualization import array_to_latex
Estados multi-cúbit#
Bases multi-cúbit#
Sea \(\{ \ket{i}\}_{i=0,1}\) la base computacional del espacio de Hilbert de un cúbit \(\Hil = {\mathbb C}^2\).
Definición:
La base computacional de \( \Hil^{\otimes n}\) está formada por todas las cadenas posibles formadas con elementos de la base de \(\Hil\)
donde \(~~ i_{n-1},...,i_0=0,1\)
La dimensión dim(\(\Hil^{\otimes n}\)) = \(2^n\) coincide con el número combinaciones distintas posibles: \(2\times 2...\times 2 = 2^n\).
Cuando representa un un ket mediante una columna de componentes, el producto tensorial se traduce en el producto de Kronecker. Por ejemplo, para un sistema de 2-cúbits, \(n=2\) y tendríamos \(2^n=2^2 = 4\) y entonces
Las etiquetas de los vectores y, por tanto, de las componentes de las matrices, bi-índices \(ij=11,12,21,22\) adoptan el mismo número, \(N^2\), de configuraciones distintas.
Notar
El multi-ínidice \(i_{n-1}i_{n-2}....i_0\) puede interpretarse como un número entero, \(p\), escrito en base binaria, que podemos traducir a base decimal
que tomará \(2^n\) valores \(p = 0,1, \, ...\, ,2^{n}-1\).
Usamos el convenio de que el número binario menos significativo está a la derecha
El cambio de notación multi-índice \(\leftrightarrow\) entero en notación decimal será frecuente. Por ejemplo \(\ket{000} = \ket{0}, \ket{111} = \ket{7}\) etc.
El vector de estado más general \(\ket{u}\in \Hil^{\otimes n}\) será una combinación lineal de elementos de la base computacional \(\ket{i_n i_{n-1}...i_1}\) en términos de unas componentes \(u_{i_ni_{n-1}...i_1}\)
donde hemos usado alternativamente la notación binaria y la decimal.
Ejemplo
Para \(n=2\) tendremos, en notación binaria
y en notación decimal, para el mismo vector
No debería haber confusión entre ambas notaciones puesto que, en cuanto aparezca un número superior a 1 quiere decir que estamos tratando con la base decimal.
Ejercicio
Normaliza el vector \(\ket{u} = (1+i)\ket{101} -2\ket{010} + 3\ket{111}\) y escríbelo en notación decimal
Circuitos multi-cúbit#
Sea un estado multicúbit de la base computacional \(q_{a} = 0,1\)
Este estado se propaga a lo largo de un circuito de forma que cada línea representa un espacio de Hilbert.
La asignación que se hace en Qibo y en Qiskit coloca el cúbit de índice binario menos relevante \(q_0\) en la línea superior. Esto es
Qiskit:

Todos los demás

Entrelazamiento#
De forma general, los estados \(\ket{u}\in \Hil^{\otimes n}\) pueden ser de dos clases:
estado factorizables, cuando \(\ket{u} = \ket{a}\otimes \ket{b}\otimes...\otimes \ket{c}\)
estados entrelazados, cuando \(\ket{u} \neq \ket{a}\otimes \ket{b}\otimes...\otimes \ket{c}\) no es factorizable
Ahora podemos usar también bases cuyo elementos sean vectores factorizados o entrelazados.
base computacional (factorizada): \(\{ \ket{00},\ket{01},\ket{10},\ket{11}\}\)
base de Bell (entrelazada):
Medidas parciales#
Una medida parcial afecta sólamente a un subconjunto de cúbits de un multi-cúbit. Aquí encontramos una diferencia crucial entre estados factorizables y entrelazados. Consideremos el estado bi-cúbit factorizable visto antes
donde vamos a suponer que el cúbit \(\ket{a}\) está en el laboratorio de Alice, y el \(\ket{b}\) en el de Bob. Una medida de Alice sobre el primer cúbit solo podrá resultar, con probabilidad \(1/2\), en uno de los dos posibles estados siguientes
Vemos que, después de esta medición, el segundo cúbit permanece intacto. Si Bob mide, podrá obtener \(\ket{0}\) ó \(\ket{1}\) con probabilidad \(1/2\).
En este caso, las medidas de Alice y Bob no están correlacionadas Sin embargo, si el estado es entrelazado, por ejemplo,
una medida de Alice sobre el primer cúbit hace colapsar estado completo a uno de los dos siguientes posibles
también con probabilidad 1/2 cada caso.
Vemos que ahora: el segundo cúbit ha sufrido modificación correlacionada con el resultado obtenido de la medida del primero
Si Alice midió \(\ket{0}\), Bob sólo puede obtener \(\ket{0}\)
Si Alice midió \(\ket{1}\), Bob sólo puede obtener \(\ket{1}\)
en este caso, las medidas de Alice y Bob sí están 100% correlacionadas. Esta correlación es independiente de la distancia que separe a Alice y a Bob, algo que parece violar causalidad. Einstein Podolski y Rosen en 1935 pensaron que este hecho indicaba que la Mecánica Cuántica era incompleta. Esto se conoce como la paradoja EPR
Notar
En ambos casos, factorizable o entrelazado, las probabilidades de Bob, de obtener \(\ket{0}\) ó \(\ket{1}\) en el segundo cúbit, son iguales a \(1/2\).
Eso implica que las correlaciones cuánticas debidas al entrelazamiento no permiten transmitir información
Sin embargo, sus efectos sí que existen. Para ponerlos de manifiesto fue necesario diseñar experimentos más sutiles. El primero que de ellos fue debido a John Bell en 1964
Puertas multi-cúbit#
Ya hemos visto en la lección de operadores que, al igual que con los vectores, los operadores pueden dividirse en dos clases esenciales: operadores factorizados y no-factorizados. Los primeros son de la forma
donde cada operador actúa de forma independiente en un sólo factor del espacio de Hilbert \(\Hil^n\).
La puerta de Walsh-Hadamard#
El operador de Waslh-Hadamard es un ejemplo de este tipo
La acción de \(W\) sobre el estado de referencia \(\ket{00...0}\) produce una superposición uniforme de todos los estados de la base.
Nota
Vamos a rescribir la acción de \(W\) de forma que no se haga inmanejable cuando \(n\) crezca. Para ello recordemos que la acción de \(H\) sobre un solo cúbit \(\ket{x} = \ket{0}\) ó \(\ket{1}\)
Entonces, usando la distributividad del producto de sumas podemos manipular
donde
Esta expresión será de gran utilidad cuando estudiemos algoritmos sencillos
Ejercicio
escribe el producto de Kronecker de dos matrices \(H\otimes H\) y verifica que sus componentes verifican
donde \(n=2 \) y \(x,y = 0,1\).
Las puertas factorizable son un conjunto muy pequeño dentro del conjunto de operadores generales sobre \(\Hil^n\). Vamos ahora a ver puertas no factorizables, primero actuando sobre \(\Hil^2\), es decir, binarias
La puerta SWAP#
La puerta SWAP es una puerta binaria fundamental, cuya acción consiste en permutar los estados existentes en los registros individuales sobre los que actúa. En particular, sobre los elementos de la base
Esto nos permite escribir el operador en la notación de producto exterior
de donde se leen las componentes de la matriz asociada
y su inserción en un circuito se representa en la forma siguiente

Puertas controladas \(\cg{U}\)#
Las puertas controladas son eficientes para generar entrelazamiento En la puerta controlada un operador se aplica sobre un cúbit dependiendo del estado en el que se encuentra otro. La representación gráfica del circuito asociado es la siguiente

El cúbit con el punto se denomina controlador, mientras que el otro es el controlado La acción de la puerta controlada se resume en la forma de Dirac siguiente
donde \(U\) es un operador unitario de 1-cúbit general. En esta forma la acción es transparente y se puede resumir en: si en el primer cúbit (controlador)
entra \(\ket{0}\), sale \(\ket{0}\) y en el segundo cúbit (controlado) no se hace nada (se aplica \(I\)).
entra \(\ket{1}\), sale \(\ket{1}\) y en el segundo cúbit (controlado) se aplica el operador \(U\).
La representación matricial de \(\cg{U}\) es fácil de obtener como suma de productos de Kronecker
con \(x,y = 0,1\).
Nota
La acción de \(\cg{U}\) sobre elementos de la base \(\{\ket{x}\}\) donde \(x=0,1\) admite una forma compacta
Escrito de esta manera es evidente que, si \(U\) es una matriz unitaria, \(\cg{U}\) también lo es \(~ \Rightarrow (\cg{U})^\dagger \cg{U} = I\). No es algo trivial por cuanto la combinación lineal de operadores unitarios, en general, no es unitaria.
Ejercicio
Escribe un operador controlado y las matrices asociadas cuando
el cúbit de control es el segundo sobre el primero.
el operador \(U\) se aplica sobre el segundo cúbit, si el estado del controlador es \(\ket{0}\).
Operadores como éste existen en circuitos clásicos. La fascinante novedad es que, ahora, por el primer cúbit podría circular una superposición \(a\ket{0} + b\ket{1}\).
En ese caso, el resultado de una acción controlada también conduce a una superposición, de forma tal que se genera entrelazamiento
Para verlo, hagamos actuar \(\cg{U}\) sobre un estado de la forma \(\ket{\phi} = (a\ket{0} + b\ket{1})\otimes \ket{U}\), que es factorizable
Vemos que, efectivamente, el resultado es un estado entrelazado

La puerta CNOT#
La puerta binaria CNOT = \(\cg{X}\) es el caso más sencillo de operador no factorizable

Sobre elementos de la base computacional \(\ket{xy}=\ket{x}\otimes\ket{y}\) donde \(\, x,y= 0,1\), su acción se puede representar de manera compacta usando la suma módulo dos
Ejercicio 1.2.1.4
el estado factorizable más general de dos cúbits es (\(a\) es la normalización)
Escribe la condición más general que deben satisfacer \(b_0,b_1,\phi_0\) y \(\phi_1\) para que CNOT\(\ket{\psi}\) sea un vector entrelazado.
La puerta CSWAP o de Fredkin#

Si el cúbit de control está en el estado \(\ket{1}\) los dos cúbits controlados se intercambian
La puerta CCNOT o de Toffoli#
La puerta CCNOT, también llamada puerta de Toffoli, es un operador sobre \(\Hil^{\otimes 3}\), en el que dos cúbits controlan la acción de \(X\) sobre un tercero
\(\Rightarrow\) sólo si ambos cúbits de control están en el estado \(\ket{11}\) el operador \(X\) actuará sobre el tercero

De nuevo, su representación es muy sencilla
Ejercicios 1.2.1.5
obtener la matriz que representa la puerta de Toffoli en la base computacional.
obtener la matriz de un circuito de 3 cúbits con una puerta CNOT en la que el tercer cúbit controla el primero. Reproducirla usando qiskit.
Puertas multiplemente controladas#
En la puerta CNOT o CX multi-controlada el operador X se activa si y sólo si los cúbits de control se encuentran en una configuración deseada.
Los botones blancos denotan controladores que se activan si el cúbit es \(\ket{0}\). Esencialmente son iguales a un controlador negro con una puerta \(X\) antes y otra después.
Por ejemplo, en este caso, la puerta \(X\) se activará si los cúbits de control se encuentran en el estado \(\ket{1100}\)

El operador asociado a esta puerta será
Nota
En qiskit existe la posibilidad de controlar una puerta arbitraria (de la clase Gate) añadiéndole el método control que acepta dos parámetros:
el primero es el número de cúbits que van a actuar como control.
el segundo, ctrl_state es un número decimal especifica el estado de control para el cual se activa la puerta. En el caso de la figura sería el número 12
Puede encontrarse información sobre las puertas controladas en qiskit en los siguiente enlaces: https://qiskit.org/documentation/stubs/qiskit.circuit.ControlledGate.html#qiskit.circuit.ControlledGate https://qiskit.org/documentation/apidoc/circuit_library.html
from qiskit import QuantumCircuit, QuantumRegister, ClassicalRegister
from qiskit.circuit.library import SwapGate, XGate
qr = QuantumRegister(5)
qc = QuantumCircuit(qr)
gateMCX = XGate().control(4,ctrl_state= 3) # puerta X 4-veces controlada
gateMCSWAP = SwapGate().control(3,ctrl_state= 4) # puerta SWAP 3 veces controlada
qc.append(gateMCX,[0,1,2,3,4])
#qc.append(gateMCSWAP,[0,1,2,3,4])
qc.draw('mpl')
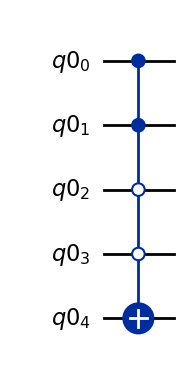
En el convenio de qiskit, efectivamente, este operador es el que se corresponde con
Circuito entrelazador para la Base de Bell#
El circuito que prepara la base de Bell \(~\{\ket{B_{xy}} \equiv \ket{xy}_B \}~\) a partir de la base computacional \(\{\ket{xy}\}\)
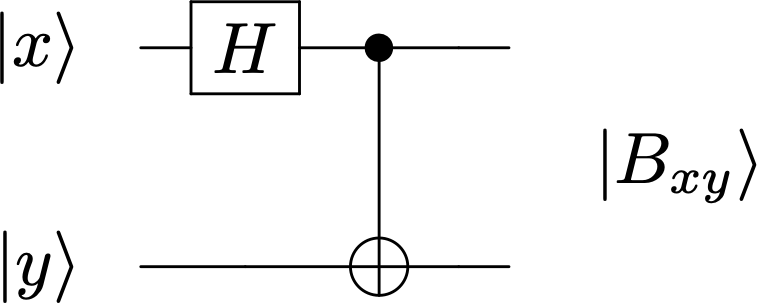
Concretamente
from qiskit import QuantumCircuit
from qiskit_aer import StatevectorSimulator
' create the circuit '
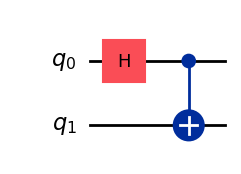
qc = QuantumCircuit(2,0)
#qc.x(0)
#qc.x(1)
qc.h(0)
qc.cx(0,1)
display(qc.draw('mpl'))
' execute in mode statevector_simulator '
Bell_state = StatevectorSimulator().run(qc).result().get_statevector(decimals=5)
from qiskit.quantum_info import Statevector
Statevector(Bell_state).draw('latex',prefix='\ket{00}_B = ')
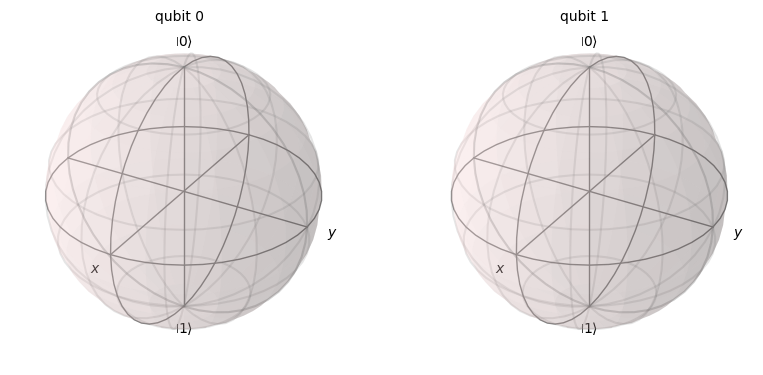
' the Bell state cannot be drawn on Bloch spheres'
Statevector(Bell_state).draw('Bloch')
Teorema de no-clonación#
El Teorema de No Clonación es uno de los resultados más sencillos y a la vez más importantes del formalismo de la Mecánica Cuántica.
De hecho su formalización completa es bastante reciente, 1982, debida a Wootters, Zurek and Dieks.
Teorema: de no-clonación
No existe un operador unitario \(U\) que, para un estado arbitrario \(|\psi\rangle\), realice la siguiente operación
Demostración:
Supondremos que \(U\) existe y llegaremos a una contradicción. Tratemos de clonar el estado \(\alpha\ket{\psi}+\beta\ket{\phi}\). Esto implica evaluar
Sin embargo, la linealidad de \(U\) nos permite seguir otro camino
Los dos resultados son diferentes y el teorema queda demostrado.
Notar
El teorema de no clonación pone de manifiesto la tensión que hay entre \(linealidad\) y \(tensorialidad\), dos propiedades fundamentales de la Mecánica Cuántica.
Es muy importante recalcar que la validez de este teorema sólo aplica a estados genéricos .
Si por ejemplo nos restringimos a estados de la base \(\ket{0}\) y \(\ket{1}\), entonces la mera puerta CNOT actúa como lo haría un operador de clonación.
