Jun 11, 2024 | 12 min read

Entrelazamiento en acción#
\( \newcommand{\bra}[1]{\langle #1|} \) \( \newcommand{\ket}[1]{|#1\rangle} \) \( \newcommand{\braket}[2]{\langle #1|#2\rangle} \) \( \newcommand{\i}{{\color{blue} i}} \) \( \newcommand{\Hil}{{\mathcal H}} \) \( \newcommand{\cg}[1]{{\rm C}#1} \) \( \newcommand{\bn}{{\bf n}} \)
Show code cell source
%run ../../macro_tQ.py
import sys
sys.path.append('../../')
import macro_tQ as tQ
import numpy as np
import scipy.linalg as la
from IPython.display import display,Markdown,Latex
import matplotlib.pyplot as plt
from qiskit.visualization import array_to_latex
Desigualdades de Bell#
Realismo local#
Las teorías con realismo local presuponen que los sistemas físicos poseen propiedades que adquieren valores bien definidos de forma independiente del observador. Así, en una teoría con realismo local, una partícula tendrá unos valores concretos de posición y velocidad en cada instante aunque nadie las observe. Toda la Física Clásica se asienta sobre las premisas de realismo local. En Mecánica Clásica, una vez definida una propiedad, sólo es cuestión de resolver las ecuaciones del movimiento para poder predecir el valor que adoptará dicha propiedad en el futuro sin necesidad de medirla.
La palabra local hace referencia a que ningún agente puede causar efectos a distancia a una velocidad mayor que la velocidad que la luz. También se usa la palabra causal en su lugar.
La Mecánica Cuántica no es una teoría con realismo local. La función de onda no describe un sistema a partir de los valores de sus propiedades. Simplemente informa de la probabilidad de obtención de distintos resultados cuando se efectúe una medida.
Si dichos resultados reflejasen propiedades del sistema, las probabilidades deberían ser estables frente a diferentes medidas suficientemente finas como para no perturbar el sistema. Pero esto no es así. La evolución del estado es determinista. Pero salvo para medidas muy particulares, en general, borra toda certeza sobre el valor de cualquier medida subsiguiente.
De hecho, medidas posteriores (las medidas son el segundo ejemplo de evolución de un vector de estado) también alteran la probabilidad de medida. Si medimos un cúbit con el observable \(Z\) y obtenemos \(+1\), el estado posteriormente será el \(\ket{0}\). Si repetimos la medida, siempre dará \(+1\). Podemos tener la tentación de pensar que la propiedad medida por \(Z\) ha quedado fijada en este valor. Eso es lo que sucedería en una teoría con realismo clásico.
Si a continuación medimos con el observable \(X\) y obtenemos también \(+1\), el estado posterior será \(\ket{+}\). Si ahora volvemos a medir con \(Z\), es 50% probable que obtengamos un \(-1\) en lugar del \(+1\) que pensábamos que había quedado fijado. Por tanto, la propiedad \(Z\) ha quedado borrada al medir la propiedad \(X\) y viceversa.
El lector avezado se percatará de que la clave está en que las medidas sucesivas se corresponden con observables que no conmutan entre sí \([X,Z]= 2i Y \neq 0\). Esta propiedad está en la base del Principio de Incertidumbre.
Desigualdades de Bell#
En 1964 físico nor-irlandés John Bell, que trabajaba en el CERN, demostró que todas las teorías que respetan el realismo local satisfacen ciertas desigualdades matemáticas. En particular, todas las leyes de la Física Clásica las satisfacen.
En contraste, John Bell mostró cómo, en Mecánica Cuántica, el entrelazamiento, incorpora correlaciones sutiles entre las medidas que permiten traspasar dichas desigualdades.
La discusión, de puramente filosófica a ser objeto de investigación experimental, culminó con el experimento de Alain Aspect y colaboradores en 1982. Con él, quedó demostrado experimentalmente que la Mecánica Cuántica, al violar las desigualdades de Bell, no es una teoría con realismo local.
La propuesta de John Bell dio pie a una familia de desigualdades que ponen en evidencia la imposibilidad de obtener ciertas correlaciones en un mundo clásico.
Vamos a examinar la desigualdad en la forma estudiada por Clauser, Horne, Shimony y Holt CHSH.
Posteriormente estudiaremos el experimento de GHZ, el cuál, también pone de manifiesto las correlaciones sutiles que introduce el entrelazamiento de una forma mucho determinista, en lugar de estadística.
Perfecta anticorrelación#
Central en esta discusión es la presencia de entrelazamiento. Vamos a seleccionar el denominado singlete de la Base de Bell.
Supongamos que Alice y Bob miden sus cúbits con el observable \(Z\)
Si Alice registra +1 quiere decir que el estado global ha colapsado a \(\ket{0}\otimes\ket{1}\). Si Bob mide a continuación, solo podrá obtener un valor \(\, -1\)
Si Alice registra -1 quiere decir que el estado global ha colapsado a \(\ket{1}\otimes\ket{0}\). Si Bob mide a continuación, solo podrá obtener un valor \(\, +1\)
En definitiva, hay una anticorrelación perfecta que se pone de manifiesto en el valor medio del producto de las medidas.
Denotemos las mediciones de Alice y Bob mediante \(a_i=\pm 1\Rightarrow b_i=\mp 1\) respectivamente. El valor medio de la variable aleatoria \(\{a_i, b_i\}\) es \(-1\)
Vamos a ver cómo la predicción teórica confirma este hecho. El estado \(\ket{11}_B\) ya es autoestado del observable asociado
Y el valor esperado satura este autovalor
Notar
La anti correlación que hemos hallado es la misma que en un experimento clásico preparado en una bolsa que contiene dos calcetines de dos colores: si Alice saca el blanco, el que saca Bob tiene que ser negro.
La cosa se pone más divertida cuando los dos aparatos de medida no se orientan en la misma dirección. El observable asociado ahora a una medición en una dirección arbitraria \(~\hat{\bf n}\) será \(~ A = \hat{\bf n}_A\cdot \boldsymbol{\sigma}\) para el detector de Alice y \(~ B = \hat{\bf n}_B\cdot \boldsymbol{\sigma}\) para el de Bob. Las mediciones en ambos detectores ¡siguen estando cuantizadas! \(a_i,b_i = 0,1\). Ello permite definir una correlación que ahora denotaremos
No hay un análogo clásico sencillo para esta medida. Sin embargo, cuánticamente, lo que esta correlación mide es el valor esperado del producto tensorial de los observables asociados
La Mecánica Cuántica es capaz de ofrecer una predicción para esta cantidad.
Teorema:
el valor medio del producto de las proyecciones de espín a lo largo de sendos ejes \(~\hat{\bf n}_A~\) y \(~\hat{\bf n}_B~\) viene dada por el coseno del ángulo \(\theta_{AB}\) que forman los ejes de los dos detectores
Ejercicio
Prueba este resultado.
Cuando los ejes son paralelos \(\hat{\bf n}_A=\hat{\bf n}_B\) recuperamos la anti-correlación perfecta
Cuando los ejes no son paralelos \(\hat{\bf n}_B\neq \hat{\bf n}_B\) sigue habiendo una correlación predicha por la Mecánica Cuántica.
La correlación se pierde totalmente sólo cuando los ejes son perpendiculares \(\hat{\bf n}_B\perp \hat{\bf n}_B\)
La desigualdad de CHSH#
Enn 1970 Clauser, Horne, Shimony y Holt CHSH propusieron una figura de mérito capaz de distinguir las correlaciones cuánticas de las clásicas.
La idea es raizar una serie de experimentos sucesivos en los que Alice y Bob pueden escoger, cada uno, dos orientaciones arbitrarias para su detector.
Para el detector de Alice las denotamos \(\hat{\bf n}_A, \hat{\bf n}'_A\) y para el de Bob \(\, \hat{\bf n}_B, \hat{\bf n}'_B.\)
Los pasos a seguir son los siguientes:
Alice y Bob seleccionan una orientación para sus detectores. Hay cuatro parejas posibles
Alice y Bob reciben un electrón cada uno de un par entrelazado en el estado \(\ket{B_{11}}\)
Alice y Bob realizan la medida de la proyección del espín a lo largo del eje elegido y anotan el resultado de la medición \((a,b)=(\pm 1, \pm 1)\)
Repiten el paso anterior un número \(i=1,..., N\) grande de veces, y con los datos obtenidos \(~(a_i,b_i)=(\pm 1, \pm 1)~\) pueden reconstruir la correlación
Repiten todo el proceso anterior para las cuatro posibles orientaciones elegidas de forma aleatoria. Con las \(4N\) mediciones construyen la cantidad
En un mundo clásico, supondríamos que los valores \(a_i,b_i\) proceden de valores predefinidos para cada sistema individual, sobre el que efectuamos simplemente un promedio estadístico de muchos sistemas. Entonces podemos probar la desigualdad de CHSH
Teorema:
La desigualdad de CHSH afirma que
Prueba
Es fácil ver que se cumple para cada colección \(a_i,a'_i,b_i,b'_i \in \pm 1\) la desigualdad
porque si \(b_i + b'_i=\pm 2\) entonces \(b_i - b'_i=0\) y viceversa. Ahora podemos demostrar la desigualdad
La Mecánica Cuántica nos proporciona una respuesta teórica para \(R\) que sólo depende de los ángulos relativos \(\cos\theta_{AB} = \cos(\theta_A-\theta_B)= \hat{\bf n}_A\cdot \hat{\bf n}_B\).
Ahora sólo hace falta jugar un poco con los detectores.
Por ejemplo, podemos situarlos en el plano \((y,z)\), perpendicular al eje de propagación \(x\), de manera que los vectores \(\hat{\bf n}'_A,\hat{\bf n}_{A},\hat{\bf n}_B\) y \(\hat{\bf n}_B'\) estén ordenados correlativamente en sentido horario. Finalmente tomaremos dos ejes coincidentes \(\hat{\bf n}_{A}=\hat{\bf n}_B\) paralelos \(\Rightarrow \theta_{AB}=0\), y apertura igual para ambos, \(\theta_{A'A} = \theta_{BB'} = \varphi\), de modo que \(\theta_{A'B'} = 2\varphi\)

Derivando vemos que esta expresión alcanza su máximo cuando \(\sin\varphi = \sin 2\varphi\) lo cual tiene solución \(\varphi = \pi/3 = 60^\circ\). Sustituyendo encontramos \(R= 2.5>2\).
Vamos a hacer una lista de ángulos relativos entre los dos polarizadores
'angulos de medida'
phi_divs = 100
phi_list=np.linspace(0,2*np.pi,phi_divs) #lista de angulos'
'lista de correlaciones C[i] a calcular'
C=[0,0,0,0]
'lista de valores de R'
R=np.zeros(phi_divs)
'Numero de medidas'
nshots = 2048
from qiskit import QuantumCircuit, Aer, execute
M_simulator = Aer.get_backend('qasm_simulator')
---------------------------------------------------------------------------
ImportError Traceback (most recent call last)
Cell In[2], line 14
11 'Numero de medidas'
12 nshots = 2048
---> 14 from qiskit import QuantumCircuit, Aer, execute
15 M_simulator = Aer.get_backend('qasm_simulator')
ImportError: cannot import name 'Aer' from 'qiskit' (/Users/javier/opt/anaconda3/envs/TalentQ2/lib/python3.11/site-packages/qiskit/__init__.py)
for j in range(phi_divs):
'ángulos de medida'
phi=phi_list[j]
'''A' = 2\phi, A = B = phi, B' = 0'''
angles_AB=[[phi,phi],[2*phi,phi],[phi,0],[2*phi,0]] # AB , A'B , AB', A'B'
for i in range(4):
'una pareja de ángulos uno para A y otro para B '
ang_AB=angles_AB[i]
'hay un circuito para cada proceso de medida'
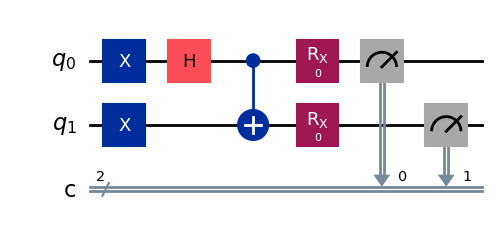
qc=QuantumCircuit(2,2)
'creamos el par de Bell B(11)'
qc.x(0)
qc.x(1)
qc.h(0)
qc.cx(0,1)
'simulamos la medida en la base de los polarizadores de A y B rotados en torno al eje x'
qc.rx(-ang_AB[0],0) # notar el valor negativo del ángulo de rotación
qc.rx(-ang_AB[1],1)
qc.measure([0,1],[0,1])
if j ==0 and i ==0:
display(qc.draw('mpl'))
' medimos '
counts=execute(qc,backend = M_simulator,shots = nshots).result().get_counts()
'construimos el correlador'
C[i]= 0
for bitstring, counts in counts.items():
C[i] += (-1)**(sum([int(bit) for bit in bitstring])) * counts/nshots
'construimos la cantidad R'
R[j]=np.abs(C[0]+C[1]+C[2]-C[3])
---------------------------------------------------------------------------
NameError Traceback (most recent call last)
Cell In[3], line 29
27 display(qc.draw('mpl'))
28 ' medimos '
---> 29 counts=execute(qc,backend = M_simulator,shots = nshots).result().get_counts()
30 'construimos el correlador'
31 C[i]= 0
NameError: name 'execute' is not defined
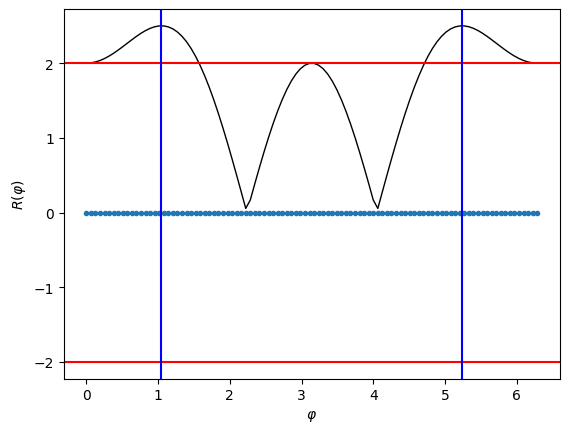
Podemos graficarlo y compararlo con el valor analítico
' función analítica '
fx= np.abs(1 + 2*np.cos(phi_list) - np.cos(2*phi_list))
plt.plot(phi_list,fx,'k-',linewidth=1)
' resultado de la simulación'
plt.plot(phi_list,R,'.')
plt.axhline(y = 2, color = 'r', linestyle = '-')
plt.axhline(y = -2, color = 'r', linestyle = '-')
' líneas horizotales en +2 y - 2'
plt.axvline(x = np.pi/3, color = 'b', linestyle = '-')
plt.axvline(x = 5*np.pi/3, color = 'b', linestyle = '-')
plt.xlabel(r'$\varphi$')
plt.ylabel(r'$R(\varphi)$')
plt.show()
Prueba con otros estados de la base de Bell. Realiza este experimento en un ordenador real.
Ejercicio
Usar bases perpendiculares de Alice \(A\perp A'\), y Bob \(B\perp B'\), y formando un ángulo \(\varphi\) entre sí.
Sin pérdida de generalidad puedes tomar \(B = X\perp Z = B'\).
Variar \(\varphi\) en el intervalo \((0,\pi)\) y hallar el valor de la máxima violación de la desigualdad de Bell.
¿Es mayor que en el ejemplo anterior? ¿Podrías hallar otra violación aún mayor?
Experimento GHZ#
Las desigualdades de Bell-CHCS demuestran que hay una manera de distinguir una teoría con realismo local de una en la que éste postulado no exista.
Lo hacen de una forma estadística: es necesario formar ciertas medias de datos sobre estados de 2-cúbits, los estados de Bell.
En 1997 Greenberger, Horne y Zeilinger estudiaron las propiedades de una serie de estados de 3-cúbits:
Es muy fácil ver que, en vez de una violación probabilística de una desigualdad, el estado GHZ conduce a una violación determinista de una igualdad.
Supongamos que:
un sistema está compuesto de tres subsistemas, \(A, B\) y \(C\).
en cada uno de ellos hay dos magnitudes observables, \(X\) e \(Y\), que al ser medidas adquieren valores binarios \(x, y = \pm 1\).
Pretendemos saber:
si existe un estado del sistema tal que, con el resultado de medidas simultáneas \(X\) o \(Y\) de cada una de sus partes \(A,B\) y \(C\) , se obtengan resultados \(x\) e \(y\) que verifiquen las siguientes ecuaciones:
Si la teoría satisface los axiomas de realismo local, los valores de \(X\) es \(Y\) estarán bien definidos independientemente de la medida que efectuemos.
Dicho de otra forma, las medidas que efectuamos son compatibles y no afectan a los resultados posibles.
Entonces podemos utilizar conclusiones que extraigamos de los resultados de un experimento para los de otro (notar que se supone que el estado es el mismo en todos los casos )
Las tres primeras afirman que \(x=1\) puesto que \(y^2=1\).
La última afirma que \(x=-1\)
vemos que hay una contradicción. Concluimos que las medidas efectuadas no son compatibles entre sí.
Como vemos, la paradoja existe en tanto en cuanto atribuyamos a las magnitudes \(X\) e \(Y\) una noción de realidad independiente de la medición.
Sólo de esta manera podemos inferir, de las tres primeras líneas, el resultado \(xxx = 1\) sin realizar una medición directa de \(XXX\) por consistencia.
La satisfacción, por tanto, de las cuatro afirmaciones, pasa por aceptar que las variables \(X\) e \(Y\), no pueden tener valores predefinidos simultáneamente en los cuatro experimentos.
Cuánticamente es fácil ver que el estado GHZ proporciona una solución al conjunto de ecuaciones.
Supongamos que \(x\) e \(y\) son los resultados de medir \(X = \sigma_x~\) y \(~Y = \sigma_y\)
Por un lado,
y, análogamente, obtenemos \(xyy=yxy=yyx= +1\).
Por otro, \(xxx=-1\) se sigue de
Inicializamos el estado GHZ

from qiskit import QuantumRegister, ClassicalRegister, QuantumCircuit, Aer, execute
qc_GHZ = QuantumCircuit(3,3)
qc_GHZ.x(0)
qc_GHZ.h(0)
qc_GHZ.cx(0,1)
qc_GHZ.cx(0,2)
qc_GHZ.draw(output='mpl')
---------------------------------------------------------------------------
ImportError Traceback (most recent call last)
Cell In[5], line 1
----> 1 from qiskit import QuantumRegister, ClassicalRegister, QuantumCircuit, Aer, execute
3 qc_GHZ = QuantumCircuit(3,3)
5 qc_GHZ.x(0)
ImportError: cannot import name 'Aer' from 'qiskit' (/Users/javier/opt/anaconda3/envs/TalentQ2/lib/python3.11/site-packages/qiskit/__init__.py)
Analicemos el valor medio de alguno de los operadores \(YYX, YXY, XYY\) ó \(XXX\)
from qiskit import Aer, execute
M_backend = Aer.get_backend('qasm_simulator')
shots=1000
'elige uno de los términos siguientes'
#multibasis = 'YYX'
#multibasis = 'YXY'
#multibasis = 'XYY'
multibasis = 'XXX'
qc_GHZ.barrier()
tQ.add_multimeasure_XYZ(qc_GHZ, multibasis)
qc_GHZ.draw(output='mpl')
---------------------------------------------------------------------------
ImportError Traceback (most recent call last)
Cell In[6], line 1
----> 1 from qiskit import Aer, execute
3 M_backend = Aer.get_backend('qasm_simulator')
4 shots=1000
ImportError: cannot import name 'Aer' from 'qiskit' (/Users/javier/opt/anaconda3/envs/TalentQ2/lib/python3.11/site-packages/qiskit/__init__.py)
Ejecuta el código anterior para las 4 posibles cadenas de Pauli
cuentas_GHZ = execute(qc_GHZ,M_backend,shots=shots).result().get_counts()
print('<'+str(multibasis)+'> =', tQ.expval_Zn_from_counts(cuentas_GHZ)[0])
---------------------------------------------------------------------------
NameError Traceback (most recent call last)
Cell In[7], line 1
----> 1 cuentas_GHZ = execute(qc_GHZ,M_backend,shots=shots).result().get_counts()
2 print('<'+str(multibasis)+'> =', tQ.expval_Zn_from_counts(cuentas_GHZ)[0])
NameError: name 'execute' is not defined
Teleportación#
El entrelazamiento conlleva un tipo nuevo de correlación que acaba constituyendo un recurso importante.
El protocolo de teleportación fue propuesto por C.Bennet,G. Brassar, C. Crepeau, R.Josza, A. Peres u W. Wooters en 1993.
Supongamos que Alice y Bob tiene dos cúbits que se encuentran en el estado entrelazado \(\ket{B_{00}}\)
Alice tiene, un segundo cúbit inicializado en un estado arbitrario \(\ket{\phi}\), y se plantea la posibilidad de transferirlo o clonarlo en el laboratorio de Bob.
El circuito de la imagen permite efectuar esa tarea
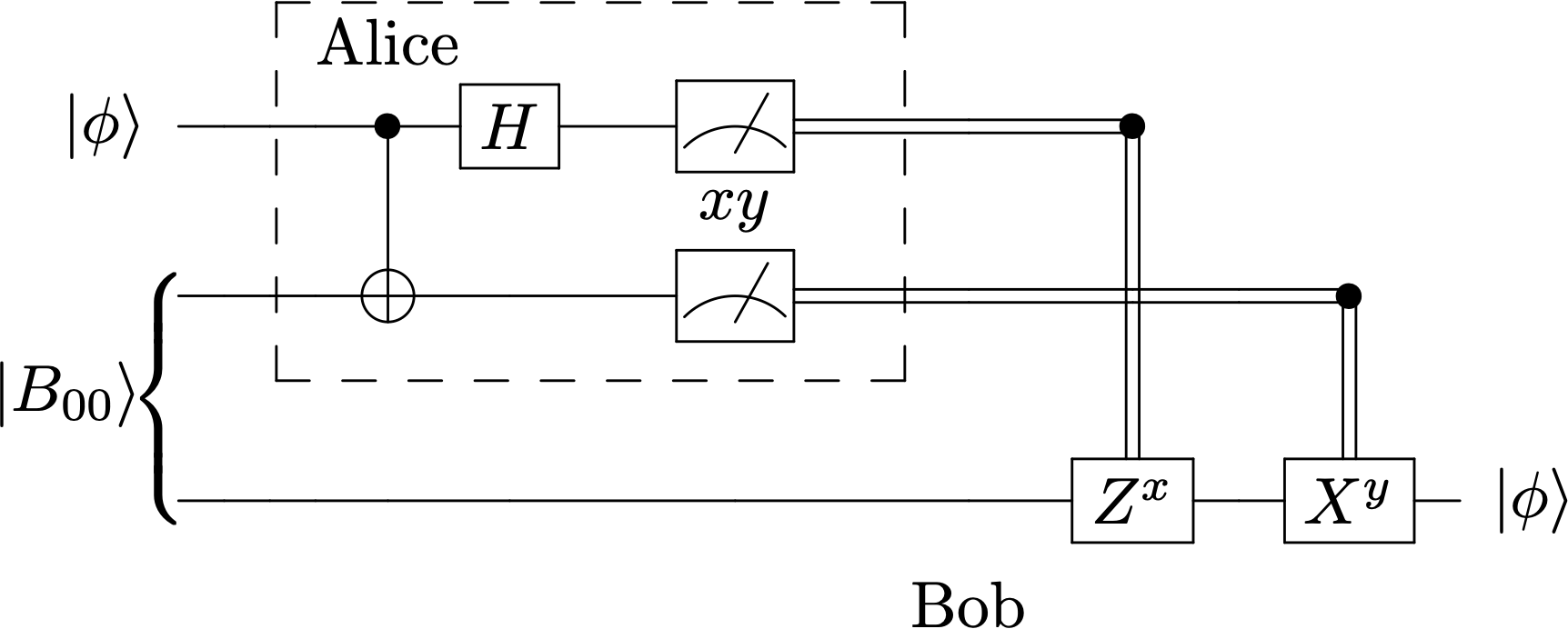
El estado inicial es
\(\rule{7mm}{0mm}\)Alice tiene acceso a los dos primeros qubits y Bob al tercero.
Alice realiza una medida de Bell a sus dos qubits, intercalando un operador \(U_{\rm desent}= (H \otimes I)\cdot U_{\rm CNOT}~\) que rota a la base de Bell
Alice mide el estado que obra en su poder, y obtiene un 2-bit clásico, \(xy\) de manera equiprobable para las 4 posibilidades.
De forma correlacionada, el cúbit de Bob colapsa a uno de entre 4 estados \(\ket{\phi_{xy}},~\) pero no sabe a cuál.
Para resolver esta ambigüedad, Alice envía el resultado de su medida \(xy\) por un canal clásico a Bob
Bob efectúa sobre su cúbit una operación controlada por este 2-bit, \(U_{xy} = X^y Z^x \).
\(\rule{7mm}{0mm}\)Como resultado de esta operación, el cúbit de Bob es finalmente \(\ket{\phi}\).
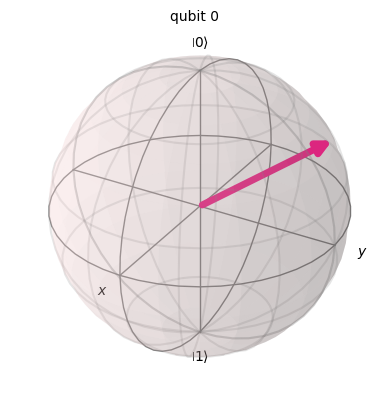
Vamos preparar el estado de Alice
# escoge dos ángulos theta y phi en la esfera de Bloch
[theta,phi]=[1.1 , 2.2]
# o hazlo de forma aleatoria
#import random
#[theta,phi] = np.array([np.pi*np.random.rand(),2*np.pi*np.random.rand()])
estado = [np.cos(theta/2),(np.exp(1j*phi))*np.sin(theta/2)]
#visualicémoslo en la esfera de Bloch
from qiskit.visualization import plot_bloch_multivector, array_to_latex
plot_bloch_multivector(estado)
Lo primero que haremos será incializar el circuito, dotado de tres cubits y dos canales clásicos en dos registros. Alice tendrá control sobre los dos primeros \(q_0, q_1\) y Bob sobre el tercero \(q_2\).
from qiskit import QuantumCircuit, QuantumRegister, ClassicalRegister, Aer, execute
qrA = QuantumRegister(2, name="qAlice")
qrB = QuantumRegister(1, name="qBob")
crx = ClassicalRegister(1, name="crx")
cry = ClassicalRegister(1, name="cry")
---------------------------------------------------------------------------
ImportError Traceback (most recent call last)
Cell In[9], line 1
----> 1 from qiskit import QuantumCircuit, QuantumRegister, ClassicalRegister, Aer, execute
3 qrA = QuantumRegister(2, name="qAlice")
4 qrB = QuantumRegister(1, name="qBob")
ImportError: cannot import name 'Aer' from 'qiskit' (/Users/javier/opt/anaconda3/envs/TalentQ2/lib/python3.11/site-packages/qiskit/__init__.py)
generamos el circuito de teleportación
# inicializa el circuito
qc = QuantumCircuit(qrA,qrB, crx, cry)
# Alice y Bob comparten un par de Bell
qc.h(qrA[1])
qc.cx(qrA[1],qrB[0])
qc.barrier()
# inyecta en el circuito el estado a teleportar
qc.initialize(estado,0)
qc.barrier()
# Añade un medidor de estados de Bell en los cúbits de Alice y efectúa las medidas
qc.cx(qrA[0],qrA[1])
qc.h(qrA[0])
qc.barrier()
qc.measure([qrA[0],qrA[1]],[0,1])
# Añade el operador X^y Z^x controlado clásicamente por las salidas x e y
qc.x(qrB[0]).c_if(cry, 1)
qc.z(qrB[0]).c_if(crx, 1)
qc.barrier()
#visualiza el circuito
qc.draw('mpl')
---------------------------------------------------------------------------
NameError Traceback (most recent call last)
Cell In[10], line 2
1 # inicializa el circuito
----> 2 qc = QuantumCircuit(qrA,qrB, crx, cry)
4 # Alice y Bob comparten un par de Bell
5 qc.h(qrA[1])
NameError: name 'qrA' is not defined
# ejecuta varias veces y observa el resultado
S_simulator = Aer.get_backend('statevector_simulator')
out_vector=execute(qc,S_simulator).result().get_statevector()
plot_bloch_multivector(out_vector)
---------------------------------------------------------------------------
NameError Traceback (most recent call last)
Cell In[11], line 2
1 # ejecuta varias veces y observa el resultado
----> 2 S_simulator = Aer.get_backend('statevector_simulator')
3 out_vector=execute(qc,S_simulator).result().get_statevector()
4 plot_bloch_multivector(out_vector)
NameError: name 'Aer' is not defined
Observa al ejecutar repetidas veces que los resultados de las medidas intermedias son aleatorios, pero el estado teleportado es siempre el correcto
El siguiente ejercicio ilustra el principio de la medida diferida.
Ejercicio
Modifica y ejecuta el circuito de teleportación de dos formas distintas
\(\rule{7mm}{0mm}\)a) Sustituyendo los controles clásicos por controles cuánticos
\(\rule{7mm}{0mm}\)b) Permutando el orden de los controles y los aparatos de medida
Discute la sutileza que distingue estas posibilidades.
Lectura recomendada: Nielsen-Chuang sección 4.4.
Ejercicio
Cambia el estado que comparten Alice y Bob por \(\ket{B_{11}}\) y modifica el circuito para que teleporte igualmente.
Nota
El protocolo de teleportación parece poner en riesgo conceptos fundamentales.
No clonación: el protocolo tiene como ingrediente esencial la medida y, por tanto, la destrucción del estado de Alice. Como consecuencia, el estado ha sido teleportado pero no clonado. Es decir, no se viola el Teorema de No Clonación .
Causalidad: el protocolo de teleportación no viola causalidad . Es necesario mandar una información clásica (como muy rápido a la velocidad de la luz) para resolver la ambigüedad que le queda a Bob. Esta parte es la que hace que la teleportación no sea un proceso instantáneo de acción a distancia.
Codificación superdensa#
Una segunda aplicación de las correlaciones que introduce el entrelazamiento permite codificar 2 bits clásicos en términos de un sólo cúbit.
Este protocolo fue propuesto por C. Bennet y S.J. Wiesner en 1992
Supongamos que Alice quiere transmitir un para de bits \(xy\in \{00,01,10,11\}\) a Bob. Ambos deben estar en posesión de un estado entrelazado que tomaremos \(\ket{B_{00}}\)
El circuito siguiente muestra el proceso
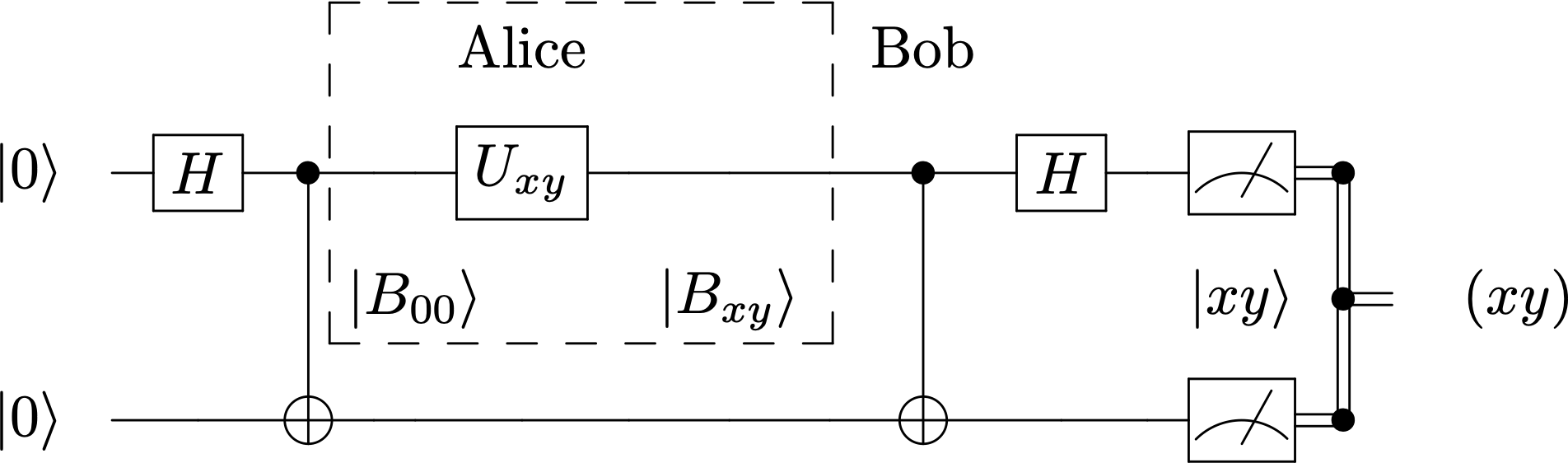
Alice comienza efectuando una operación en su laboratorio sobre el cúbit que maneja, que depende del 2-bit \(xy\) que quiere enviar
\(\rule{7mm}{0mm}\)Una vez efectuada esa operación, el estado que comparten es \(\ket{B_{xy}}\).
Alice envía a Bob su parte del estado entrelazado a través de un canal cuántico.
Ahora Bob está en posesión del estado \(\ket{B_{xy}}\) y sólo necesita hacer una medida de Bell sobre el estado que posee para recuperar la etiqueta \(xy\)
Intercambio de entrelazamiento#
Ya hemos visto cómo el ejemplo más sencillo de entrelazamiento tiene una aplicación muy interesante en la teleportación. Vamos a ver que el entrelazamiento se puede contagiar a terceras partes. En inglés se denomina entanglement swapping.
Consideremos el siguiente circuito
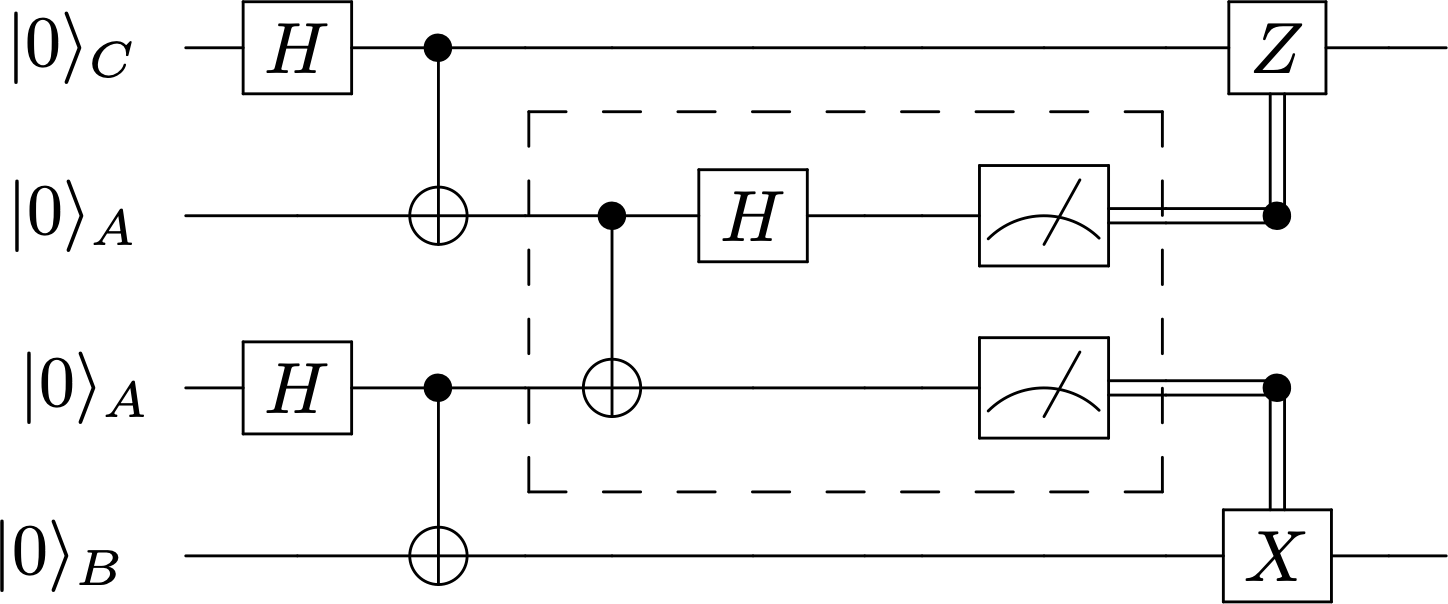
Alice (A) entrelaza un cúbit con Charles © y otro con Bob (B).
Después, Alice hace una medida de Bell, y comunica el resultado \(xy\) a Charles y a Bob respectivamente,
los cuales efectúan las puertas controladas \(Z^x\) y \(X^y\) respectivamente.
El estado a la salida es \(\ket{B_{00}}_{CB}\) de Bell compartido por Bob y Charles.
Ejercicio
Programa el circuito de la figura.
Ejecuta varias veces el circuito y muestra que el estado final que comparten Bob y Charles está entrelazado. ¿Es siempre el mismo estado?
Completa el circuito para que sea capaz de teleportar un cúbit arbitrario entre Charles y Bob.
LOCC#
Bajo la denominacióm de Operaciones Locales y Comunicación Clásica se denomina un método en Teoría Cuántica de la Información, mediante el cual,
una operación local es efectuada en una parte del sistema.
el resultado es comunicado clásicamente a otra del sistema
en esa otra parte se fectúa también una operación local, condicionada al resultado comunicado clásicamente.
Al algoritmo de teleportación es un ejemplo de LOCC en el cuál
Alice realiza una medida de Bell
Bob actúa localmente con \(X\) o \(Z\) dependiendo del resultado comunicado clásicamente.
En el intercambio de entrelazamiento vemos que LOCC se puede utilizar para transformar un estado entrelazado en otro estado entrelazado.
En este caso un estado de Bell entre Alice y Bob pasa a otro estado de Bell entre Charles y Bob
